Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ярославский Государственный Технический Университет

Предмет:

Высшая математика

Файл:

Математика высшая

.pdf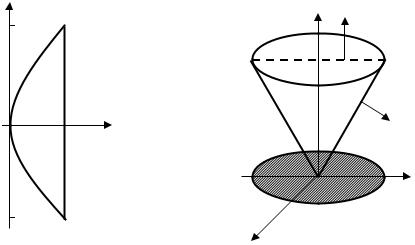

Скачиваний:

Добавлен:

15.05.2015

Размер:

1.35 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 158 9 10 11 12 13 14 15 > Следующая >>>

НГАВТ - Стр 14 из 45

y = −2 и y = 2 соответственно. Левой границей области является кривая x = y2 / 4 (уравнение параболы y2 = 4x разрешено относительно x ), а правой

— прямая x = 1 . Таким образом, двойной интеграл I с измененным порядком

интегрирования запишется в виде

		2	1
		I = ò dy ò f (x, y)dx.
		−2	y2 / 4
Пример 2. Вычислить тройной интеграл I = òòò (-2x)dV , если область V
			V
ограничена поверхностями σ 1 : z = 2 и σ 2 : z2 = x 2 + y2 (z ³ 0) (рис. 13).
Решение. Исключая z		из уравнений σ 1 и σ 2 , получим уравнение границы
области Dxy	(проекции V на плоскость xOy ): x 2 + y2 = 4 . Для вычисления
интеграла I	переходим к	цилиндрическим координатам по формулам (4) с

пределами	интегрирования		0 ≤ ϕ ≤ 2π , 0 ≤ ρ ≤ 2, ρ ≤ z ≤ 2			( z = ρ
уравнение верхней части конуса			z2	= x 2 + y2 в цилиндрических координатах).
По формуле (5) получаем
I = òòò (−2z)dV = òòò (−2z)ρ dρdϕdz
V		V
2π	2	2	2π	2	2
= − ò dϕ ò ρ dρ ò 2zdz = − ò dϕ ò ρ (z 2					)dρ =
0	0	ρ	0	0	ρ

2π 2 2π

= − ò dϕ ò ρ (4 − ρ 2 )dρ = − ò

0 0 0

			ρ 2	2			2π
	2
	2
((2ρ		−		)	)dϕ = −4		ò dϕ = −8π .
((2ρ		−	4	)	)dϕ = −4		ò dϕ = −8π .
			4	0			0
				0			0
					Z	n2

Dxy

НГАВТ - Стр 15 из 45

Рис. 12

Рис. 13

Пример 3. Вычислить поверхностный интеграл

I = òò

z 3

dσ ,

+ y

+ z

σ 2

где σ 2 — внешняя часть конуса

= x2

+ y2

(z ³ 0) , отсекаемая плоскостью

z = 2 (рис. 13).

σ 2

проецируется в область Dxy

Решепие.

Поверхность

однозначно

плоскости xOy , и интеграл вычисляется по формуле (7).

Единичный вектор внешней нормали к поверхностях σ 2

найдем по формуле

(8):

2xi + 2 yj - 2zk

xi + yj - zk

= ±

4x 2 + 4 y2 + 4z 2

x 2 + y2 + z 2

Здесь в выражении для нормали выбран знак плюс,

так как угол γ между осью

Oz и нормалью

— тупой

и,

следовательно,

cos γ

= ±

(-z)

x 2 + y2 + z 2

на поверхности σ 2

должен быть отрицательным. Учитывая, что z =

x 2 + y2

получаем

I = òò

z 3

dxdy

= òò z

dxdy =

+ y

+ z

z /

+ y

+ z

Dxy

= òò ( x 2 + y2 )dxdy.

Dxy

Область Dxy

есть круг

x 2 + y2 £ 4 . Поэтому в последнем интеграле переходим

к полярным координатам (при этом 0 ≤ ϕ ≤ 2π , 0 ≤ ρ ≤ 2 ):

НГАВТ - Стр 16 из 45

2π

I = òò ρ 2 × ρ dρdϕ = ò dϕ ò ρ 3 dρ = ò

÷dϕ = 4

ò dϕ = 8π .

Dxy

yi - xj - z

k .

Пример 4. Найти дивергенцию и ротор векторного поля a

Решение. По формуле (9) получаем

diva =

y +

(- x) +

(-z

) = -2x.

¶x

¶y

¶z

Ротор данного векторного поля находим по формуле (10):

rota

¶x

¶y

¶z

- z 2

æ ¶

(-z 2 ) -

ör

-z 2 ) -

ö r

= ç

(- x)÷i

(

y÷ j

¶y

¶z

è ¶x

¶z ø

ö r

+ ç

(- x) -

y÷k

= -2k .

¶x

¶y

Пример 5. Вычислить		поток векторного поля a = yi - xj - z 2 k						через
замкнутую поверхность σ , образованную плоскостью						z = 2 и частью конуса
z2 = x 2 + y2 (z > 0) .	Проверить		результат		с	помощью	формулы
Остроградского.					поверхностей: σ 1
Решение. Поверхность		σ состоит	из	двух	поверхностей: σ 1		—	части
плоскости z = 2 и σ 2	— части конуса		z2	= x 2 + y2		(рис. 13). Поэтому поток
через σ равен сумме потоков вектора a через составляющие поверхности:
П = П1 +		r	r		r	r
П = П1 +		П 2 = òò (a, n1 )dσ + òò (a, n2 )dσ ,
		σ 1			σ 2

где n1 и n2 — внешние нормали к плоскости и конусу соответственно.

Для поверхности z = 2 в силу формулы (8) получим n1 = k и,

НГАВТ - Стр 17 из 45

следовательно,

òò (-z

)dσ = -4òò dxdy =

П1 = òò (a, n1 )dσ =

σ 1

Dxy

2π

2 ö

2π

= -4

dϕ

ρ dρ = -4

(ρ / 2)

dϕ = -16π ,

÷dϕ = -8

так как на поверхности σ 1

имеем z = 2 .

σ 2

Вычислим поток через поверхность

уравнение которой в явном виде

дается

соотношением

z =

x 2 + y2

вектор

внешней нормали равен

xi + yj - zk

. По формуле (11) получаем

x 2 + y2 + z 2

r r

xy - xy + z 3

2 = òò (a, n2 )dσ =òò

dσ =

+ y

+ z

σ 2

= òò

z 3dσ

=8π

+ y

+ z

σ 2

(см. пример 3).

Таким

образом,

поток

векторного

поля

через

поверхность

σ = σ 1 + σ 2 равен

П = П1 + П 2 = -16π + 8π = -8π .

Найдем решение этой задачи с помощью формулы Остроградского (13).

Дивергенция поля a = yi - xj - z 2 k

равна diva = −2z (см. пример 4), и поток

= òòò (-2z)dV = -8π ,

П = òòò divadV

как это было вычислено в примере 2.

Пример 6. Вычислить циркуляцию векторного поле

a = yi - xj - z 2 k

контуру

Г ,

образованному

пересечением

поверхностей

σ 1 : z = 2

σ 2 : z2

= x 2

+ y2

(z ³ 0) . Проверить результат с помощью формулы Стокса.

Решение.

Пересечением указанных

поверхностей

является окружность

НГАВТ - Стр 18 из 45

x 2 + y2 = 4, z = 2 (рис. 13). Направление обхода контура выбирается обычно так, чтобы ограниченная им область оставалась слева. Запишем параметрические

уравнения контура Г :
ìx = 2cos t,		ìdx = -2sin tdt ,
ï		ï		(15)
í y = 2sin t, откуда		í dy = 2 cos tdt,
ï	z = 2,	ï	dz = 0,
î		î

причем параметр t изменяется от 0 до 2π . По формуле (12) с учетом (6) и (15)

получаем

2π

Ц = ò Pdx + Qdy + Rdz = ò 2sin t(-2sin t)dt - 2cos t × 2cos tdt - 4 × 0 =

	Г	0
=	2òπ (-4 sin2 t - 4 cos 2 t)dt = -4		2òπ dt = -8π .
	0		0
	Применим теперь формулу Стокса (14). В качестве поверхности σ ,
натянутой на контур		Г , можно взять часть плоскости z = 2 . Направление

нормали n = k к этой поверхности согласуется с направлением обхода контура

Г . Ротор данного векторного поля вычислен в									примере 4: rot a = -2k .
Поэтому искомая циркуляция
Ц = òò						r r		òò (-2k, k )dσ =
Ц = òò		(rot a, n)dσ =						òò (-2k, k )dσ =
σ								σ
								2π	2
= -2òò dσ = -2òò ρdρdϕ = -2 ò dϕ ò ρdρ =
σ							Dxy	0	0
2π æ			ρ	2	2		ö	2π
2π æ				2	2		ö	2π
= -2 ò	ç						÷	ò dϕ = -8π ,
	ç						dϕ = -4
		2					dϕ = -4
		2					÷
0 è						0	ø	0
0 è						0	ø	0

что совпадает со значением циркуляции, полученным непосредственным вычислением.

КОНТРОЛЬНАЯ РАБОТА № 6

РЯДЫ

НГАВТ - Стр 19 из 45

Основные теоретические сведения

1. Числовой ряд

∞
a1 + a2 + ... + an + ... = åan ,	(1)

n=1

называется

∞

Sn = åak .

k =1

сходящимся, если существует предел его частичных сумм

Число	S = lim Sn называется суммой ряда. Если же предел
	n→ ∞

частичных сумм не существует, то ряд (1) называется расходящимся. Необходимый признак сходимости: если ряд (1) сходится, то его общий член

стремится к нулю при n ® ¥ : lim an = 0.
				n→ ∞
К достаточным признакам сходимости рядов с положительными членами
(an ³ 0)	относятся:
а) Признак сравнения в предельной форме: если
		lim	an	= k (k ¹ 0, ¥),	(2)
		lim		= k (k ¹ 0, ¥),	(2)
		n→∞ bn
	∞	∞
то ряды	åan и	åbn одновременно сходятся или расходятся. В качестве
	n=1	n=1

эталонных рядов для сравнения обычно служат:

∞		1
ряд å		1	, сходящийся при a > 1 и расходящийся при a £ 1			;
ряд å		a	, сходящийся при a > 1 и расходящийся при a £ 1			;
n=1	n
∞
ряд åqn−1 сходящийся при 0 £ q < 1 расходящийся при q ³ 1 .
n=1
n-l
б) Признак Даламбера: если существует
			lim	an+1	= q,	(3)
			lim		= q,	(3)
			n→∞	an
∞
тo ряд åan		сходится при 0 £ q < 1 и расходится при q > 1 . Если же q = 1, то

n=1

вопрос о сходимости ряда этим признаком не решается.

НГАВТ - Стр 20 из 45

∞

Ряд åan

с членами, имеющими разные знаки,

называется условно сходя-

n=1

∞

щимся,

если ряд

åan сходится, а ряд

расходится, и

абсолютно

n=1

∞

сходящимся, если ряд å

сходится.

n=1

∞

в) Признак Лейбница: если члены ряда

åan

удовлетворяют условиям:

an an+1 < 0

n=1

> ... >

> ... ; 3)

(т.е. ряд знакочередующийся); 2)

lim

= 0 , то ряд сходится. Погрешность

, происходящая от замены суммы

n→∞

сходящегося знакочередующегося ряда суммой его первых

членов, по

абсолютной величине меньше первого из отброшенных членов:

S − Sn

an+1

(4)

Ряд вида

∞

a0 + a1 ( x − a) + ... + an ( x − a)n + ... = åan ( x − a)n

(5)

n=0

называется степенным рядом (относительно ( x − a) ), точка

x = a центром

разложения, an — коэффициентами ряда. Число R называется радиусом сходимости степенного ряда, если ряд (5) сходится при x − a < R и расходится при x − a > R . При x − a = R ряд может как сходиться, так и расходиться.

Интервал ]a − R, a + R[ называется интервалом сходимости степенного ряда

(5). Радиус сходимости R может быть найден по формуле

R = lim		an	.	(6)
	an+1
n→∞

Степенной ряд (5) внутри интервала сходимости можно почленно дифферен- цировать и интегрировать с сохранением радиуса сходимости.

3. Степенным рядом с комплексными членами называется выражение вида

НГАВТ - Стр 21 из 45

∞

a0 + a1 z + a2 z 2 + ... + an z n + ... = åan zn ,

n=0

где zn = xn + iyn , an

комплексные постоянные. Областью сходимости этого

ряда является круг с

центром в начале координат:

< R , где

R — радиус

сходимости ряда.

По определению,

e z = 1 + z +

z 2

+ ... +

z n

+ ..., R = ∞;

z 2n

cos z = 1 −

z 2

− ... + (−1)n

+ ..., R = ∞;

(7)

(2n)!

sin z = z −

z 3

− ... + (−1)n

z 2n+1

+ ..., R = ∞;

(2n + 1)!

Отсюда следует, что

= e x + iy = e x (cos y + i sin y).

e z

(8)

4. Рядом Фурье периодической функции

f ( x), − l ≤ x ≤ l, называется ряд

вида

∞

nπx

f ( x) =

åan cos

+ bn sin

n=1

nπx

an =

−òl

f ( x) cos

dx,

n = 0, 1, 2, ...;

nπx

n = 1, 2, ...;

f ( x) sin

dx,

−òl

Функция, заданная на полупериоде [0, l], может быть представлена различ- ными рядами Фурье. При четном продолжении данной функции на второй полупериод [0,−l) получается ряд по косинусам:

	a0	∞	nπx
f ( x) =		åan cos		;	(9)
			l
2		n=1

НГАВТ - Стр 22 из 45

	2	l		nπx
		ò
bn = 0; an =	l	ò	f ( x) cos	l	dx, n = 0, 1, 2, ...;
bn = 0; an =		−l	f ( x) cos		dx, n = 0, 1, 2, ...;
		−l

а при нечетном продолжении — ряд по синусам:

∞

nπx

f ( x) = åbn

sin

; an = 0;

n=1

nπx

bn =

f ( x) sin

dx,

n = 1, 2, 3, ...;

−òl

Пример 1. Исследовать на сходимость числовой ряд

∞ arctg (2n + 3)

n=1

Решение. Проверяем сходимость ряда по признаку Даламбера (3). Так как

общий член ряда an =

arctg (2n + 3)

, то, заменяя в выражении n -го члена n

на n + 1 , находим an+1 =

arctg (2n + 5)

Затем ищем предел отношения

n + 1

последующего члена an+1 к предыдущему an

при n → ∞ :

q = lim

an+1

= lim

n × arctg (2n + 5)

= 1.

n→∞

n→∞ (n + 1)arctg (2n + 3)

Поскольку полученный предел равен единице, признак Даламбера не дает ответа на вопрос о сходимости ряда (здесь для вычисления предела было использовано правило Лопиталя). Применим теперь признак сравнения в предельной форме. В

			∞	1			1
качестве эталонного ряда выберем ряд å						, bn =		и в силу формулы (2)
качестве эталонного ряда выберем ряд å					n	, bn =	n	и в силу формулы (2)
получим			n=1		n		n
получим
k = lim	an	= lim	arctg (2n + 3)	= lim arctg (2n + 3) =					π .
k = lim		= lim	n ×1	= lim arctg (2n + 3) =					π .
n→∞ bn		n→∞	n ×1			n→∞			2

Следовательно, исследуемый ряд является расходящимся, так как эталонный ряд с

НГАВТ - Стр 23 из 45

общим членом bn

и расходится (гармонический ряд).

Пример

Найти

радиус

и интервал

сходимости

степенного ряда

∞

n + 3

( x

+ 2)n .

Исследовать

сходимость

ряда на

концах

интервала

+ 1

n=0

сходимости.

Решение. Радиус сходимости находим по формуле (6):

R = lim

= lim

(n + 3)((n + 1)2 + 1)

= 1.

an+1

(n + 4)(n2 + 1)

n→∞

Интервал сходимости данного ряда определяется неравенством

x + 2

< 1

или − 3 < x < −1

Исследуем концы интервала сходимости. При x = −1 получаем числовой

ряд

∞

n + 3

∞

n + 3

(−1 + 2)n =

+ 1

n=0

предельного признака сравнения (эталонный пряд — гармонический).

При x = −3 получаем числовой знакочередующийся ряд

∞

n + 3

∞

n + 3

(−3 + 2)n = å

(−1)n

+ 1

n=0

который сходится

по

признаку Лейбница.

Так

как

ряд,

составленный

из

∞

n + 3

абсолютных членов

данного

ряда, т. е. ряд

, расходится,

то

+ 1

n=0

исследуемый ряд, сходится условно.

Таким образом, интервал сходимости исследуемого степенного ряда имеет вид − 3 ≤ x < 1 .

0		dx
Пример 3. Вычислить I = ò		dx		с точностью до 0,001.

	3
	3	1 + x	2
−0,6		1 + x

Решение. Разложим подынтегральную функцию в биномиальный ряд по степеням x :

<<< < Предыдущая 1 2 3 4 5 6 78 / 158 9 10 11 12 13 14 15 > Следующая >>>