Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ярославский Государственный Технический Университет

Предмет:

Высшая математика

Файл:

Математика высшая

.pdf

Скачиваний:

Добавлен:

15.05.2015

Размер:

1.35 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 159 10 11 12 13 14 15 > Следующая >>>

НГАВТ - Стр 24 из 45

(1 + x 2 )

− 1

= 1 -

x 2 +

1× 4

x4 -

1× 4 × 7

+ ...,

< 1.

3 × 6

×9

Таж как отрезок

интегрирования

[−0,6; 0]

находится

внутри интервала

сходимости биномиального ряда, то ряд можно почленно интегрировать.

Подставляя в интеграл вышеприведенное разложение подынтегральной функции и почленно интегрируя в указанных пределах, получаем

0				dx						0				1				2		14
I = ò				dx				=		ò (1 -				1	x 2	+		2	x4 -	14	x6	+ ...)dx =
	3													3				9		81
	3		1 + x				2
−0,6			1 + x						−0,6
æ		1				3		2				5		14				7	ö	0
æ		1				3		2				5		14				7	ö	0
= ç x -					x		+				x		-				x		+ ...÷		=
= ç x -	3 ×			3	x		+	9 ×		5	x		-	81 × 7			x		+ ...÷		=
è	3 ×			3				9 ×		5				81 × 7					ø	−0,6
è																			ø	−0,6

æ			(0,6)3				2 × (0,6)5		14 × (0,6)7	ö
ç	- 0,6	+				-		+		÷
ç										÷
= -ç			9				45		567	- ...÷.
è			9				45		567	ø
Четвертый член	14 ×	(0,6)		7	» 0,0007 меньше 0,001					. Поэтому согласно
Четвертый член	14 ×	567			» 0,0007 меньше 0,001					. Поэтому согласно
		567

неравенству (4) для вычисления приближенного значения интеграла с требуемой точностью достаточно ограничиться первыми тремя членами ряда:

I = 0,6 -

(0,6)3

2 × (0,6)

» 0,579.

Пример 4. Найти сумму ряда с комплексными членами:

1 + πi - π 2

π 3

i +

π 4

π 5

i - ... .

Решение. Общий член данного ряда имеет вид

π n

(πi)n

т. е. ряд, по определению, является

функцией

f (z) = e z при z = πi

[см.

формулу (7)]. Следовательно,

сумма

этого

ряда равна

значению функции

f (z) = e z в указанной точке: eπi

= cosπ + i sinπ = −1

[см. формулу

(8)].

НГАВТ - Стр 25 из 45

∞		(πi)n
Таким образом, получаем å			= -1 .

n=	0	n!

Прамер 5. Разложить периодическую функцию f (x) = x − 1 , 0 ≤ x ≤ 3 в ряд Фурье по косинусам. Построить график функции.

Решение. Данная функция определена на полупериоде [0, 3] , т. e. l = 3 .

Для разложения такой функции в ряд Фурье по косинусам ее следует продолжить на второй полупериод [−3,0) четным образом (рис. 14). Для четной функции

коэффициенты bn = 0 коэффициенты an

вычисляются по формулам (9):

Рис. 14

2-3l

-1 nπx

213

nπx

f ( x) cos

dx =

x - 2

cos

dx.

l ò0

3 ò0

Так как

ìx - 1 при x ³ 1,

x- 1 = íî- ( x - 1) при x < 1,

то отрезок интегрирования разобьем на два отрезка: от 0 до 1 , где										f ( x) = − x + 1
и от 1 до 3 , где	f ( x) = x − 1 . Тогда
		2	æ 1			nπx	3	nπx		ö
			ç							÷
an	=		ç	ò(1	- x) cos		dx + ò( x - 1) cos			÷
an	=	3	ç	ò(1	- x) cos	3	dx + ò( x - 1) cos	3	dx ÷.
		3	è	0		3	1	3		ø

При n = 0 имеем
		2	æ 1		3	ö
a0	=		ç	ò(1		÷	=
			ç			÷
		3	ç		- x)dx + ò( x - 1)dx ÷
		3	è	0	1	ø

НГАВТ - Стр 26 из 45

(1 - x)

( x - 1)

3 ö

2÷

1 ø

Для

вычисления

коэффшаиентов

(n = 1, 2, ...)

применим

метод

интегрирования по частям:

ò udv = (uv)

- ò vdu,

причем

в первом

интеграле

примем

u = 1 - x, dv = cos

nπx

откуда

du = -dx, v =

sin

nπx

u = x − 1,

Во втором

интеграле положим

nπ

dv = cos

nπx

, откуда

du = dx, v =

sin

nπx

. Тогда

nπ

nπx

(1 - x) sin

sin

πn

nπ

nπx

( x - 1) sin

òsin

πn

nπ

nπx

3 ö

cos

π 2 n2

1 ø

- cos

nπx

+ 1

+ cos nπ - cos

nπ ö

π 2 n2

6 æ

nπ

6 æ

nπ ö

çcos nπ + 1

- 2cos

ç(-1)

+ 1

- 2cos

÷,

π 2 n2

так как cos nπ = (-1)n .

Следовательно, искомое разложение функции в ряд Фурье по косинусам

имеет вид

НГАВТ - Стр 27 из 45

∞

nπx

f ( x) =

åan cos

n=1

∞

nπ ö

nπx

+ å

ç(-1)

+ 1 - 2cos

÷ cos

n=1

Это разложение справедливо в области непрерывности данной функции.

ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ

КОНТРОЛЬНАЯ РАБОТА № 4

I. Найти неопределенные интегралы. Правильность полученных результатов проверить дифференцированием.

xdx

1. 1) ò 7 + x2 ;

2. 1) ò	dx		;
	2	x
	sin
		5

3.1) ò 5dx- x2 ;

4.1) ò 5xdx+ 3 ;

5.1) òsin(2 - 3x)dx;

x − 2dx;

òe

6. 1)

7. 1)

;

7 + 4x2

8. 1)

;

cos2 2x

9. 1)

cosç

4÷dx;

2)	ò	( x + 18)dx				;
2)	ò	x2 - 4x - 12				;
2)	ò	( x + 4)dx	;
2)	ò	x2 - 2x - 8	;
2)	ò	( x + 23)dx			;
2)	ò	x2 + x - 20			;
	ò	( x + 12)dx
2)	ò	x2 - x - 6 ;
2)	ò	( x + 19)dx				;
2)	ò	x2 - 2x - 15				;
2)	ò	(5x + 6)dx				;
2)	ò	x2 + 4x - 12				;
2)	ò	(5x - 7)dx		;
2)	ò	x2 - x - 20		;

5xdx

2)ò x2 + x - 6 ;

(5x + 2)dx 2) ò x2 + 2x - 8 ;

3) ò(3 - x) cos xdx;

3) ò x ln(1 - 3x)dx;

3) ò xe −7 x dx;

3) òarctg 4xdx;

3) ò x3 ln xdx;

3) ò x sin 5xdx;

3) ò(2x + 5) sin xdx;

3) ò ln xdxx ;

3) òarcsin 3 dx;

НГАВТ - Стр 28 из 45

10. 1) ò 3(2x + 1) ;

11.1) ò e x dx ;

3 1 − e x

12.1) ò x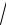3 − x2 dx;

13.	1)	ò	arctgxdx	;
			1 + x2
14.	1)

òsin 2x 2 − cos2 xdx;

15. 1)	ò	sin xdx						;
		1 − cos x
		3			dx
16. 1)	ò		ln x					;
			x

	ò	1 − tgx
17. 1)		cos2 x dx;
		2
18. 1)	ò	x				dx;
		8 + x3
19. 1)	ò		sin 2x						dx;
		cos2		x + 3
	ò	x2dx
20. 1)							;
		cos2		x3

(5x + 1)dx 2) ò x2 + 2x − 15 ;

19− 4x

2)ò 2x2 + x − 3 dx;

		ò	2x + 9
2)							dx;
			x2 + 5x + 6
		ò	x + 9
2)							dx;
			x2 + 2x − 3
		ò	2x + 27
2)						dx;
			x2 − x − 12
2)		4x + 31
ò
					dx;
	2x2 + 11x + 12
		ò	11x − 2
2)				dx;
			x2 + x − 2

17− 2x

2)ò x2 − 5x + 4 dx;

	ò	9 − 2x
2)			dx;
		x2 − 5x + 6
	ò	4x + 27
2)			dx;
		2x2 − x − 6
	ò	x − 13
2)			dx;
		x2 − 2x − 8

II. Вычислить определенный интеграл.

3) ò xe 3 x dx;

3) ò(5x − 2) ln xdx;

3) ò x cos2 2xdx;

3) òln(3 + x2 )dx;

3) ò x arcsin xdx;

3) ò(2 − x) sin xdx;

3) ò(1 − ln x)dx;

3) ò(3x + 4)cos xdx;

3) òarcctg (4x)dx;

3) ò x ln2 xdx;

3) ò x2 sin 3xdx;

	7					0
	7		x + 2dx			0			3xdx
1.	ò		x + 2dx		2.	ò			3xdx
				x
									( x + 1)		3
	2					− 3	4		( x + 1)
							4
	1			dx		0		dx
3.	1		x	dx	4.	0		dx
	ò0	4 − x				−ò8 5
								− 3 x2
								− 3 x2
	7		dx			1			xdx
5.	ò		dx		6.	ò			xdx

			x − 3					(5 − x)		3
	2		x − 3			−4		(5 − x)

НГАВТ - Стр 29 из 45

		0							dx									1			dx
									dx								8.				dx

7.	−ò3 4 2 − 1 + x
7.	−ò3 4 2 − 1 + x																−ò1 8 + 3 x2
		0							dx									0			dx
									dx								10.				dx

9.	−1ò4 1 + 3x + 1																	−ò1		4 + 3 x2
9.	−1ò4 1 + 3x + 1																	−ò1		4 + 3 x2
		4																6
		4				xdx												6			x − 3
11.		ò				xdx											12.	ò			x − 3			dx
11.		ò			4 + x												12.	ò						dx
		0			4 + x													3			x
		3																1
		3		x2 +								1 +			x			1					x − 2
13.		ò		x2 +								1 +			x	dx	14.	ò					x − 2			dx

																			1 + x −						2
		0						1 + x										2	1 + x −						2
		49					dx											1			xdx
15.		49				x	dx										16.	1			xdx
		25ò x − 6																ò0
																					2x + 7
																					2x + 7
		0																9					dx
		0		3					x		2							9
17.		ò		3					x					dx			18.	ò
				3																	x ( x − 1)
				3		2							3
		−8				x			+				3					4
		2					dx											4			dx
19.		ò1					dx										20.	ò0			dx
			2 + 4																			+ 5
			2 + 4							x − 1											x	+ 5

III. Вычислить несобственный интеграл или установить его расходимость.

∞

ò xe − x2 dx

x + 3

−3

∞

òe

ò4

x ln2 x

( x − 4)2

xdx

∞

ò tgxdx

x − 1

−π 2

π 4 cos xdx

∞

òe

sin2

ò0

x2 + 2x + 5

10.

ò ctgxdx

( x +

∞

11. ò0

12. ò0

9x2 + 1

1 − x2

НГАВТ - Стр 30 из 45

	8	3x + 2								∞
13.	ò				dx		14.			òe−5 x dx
		3
		3		x
	0			x						0
	8		dx							0
	ò		dx							òe− x			2	xdx
													2
15.							16.
15.		x ln3 x					16.
	0									− ∞
	0			dx						∞		dx
17.	−ò1			dx				18.		ò0		dx
											4x2			+ 1
			( x + 1)3								4x2			+ 1
	−4			dx						∞		dx
19.	ò			dx					20.	ò		dx
											4
		3 ( x +			5)	4					4	x + 2
	−5	3 ( x +			5)					14		x + 2

IV. Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж области.

1.	3x2 − 4 y = 0, 2x − 4 y + 1 = 0
2.	3x2 + 4 y = 0, 2x − 4 y − 1 = 0
3.	2x + 3 y2 = 0, 2x + 2 y + 1 = 0
4.	3x2	− 4 y = 0,	2x + 4 y − 1 = 0
5.	3x2	+ 4 y = 0, 2x + 4 y + 1 = 0
6.	2x − 3 y2 = 0,		2x + 2 y − 1 = 0
7.	3x2	− 2 y = 0, 2x − 2 y + 1 = 0
8. 4x + 3 y2 = 0, 4x + 2 y + 1 = 0
9.	3x2 − 2 y = 0,		2x + 2 y − 1 = 0

10.	4x − 3 y2 = 0, 4x + 2 y − 1 = 0
11.	y = x3 + 3,		x = 0,	y = x − 1,	x = 2
12.	y = x3 + 2,		x = 0,	y = x − 2,	x = 2
13.	y = x3 + 1,		x = 0,	y = x − 3,	x = 2
14.	y = x3 − 1,		x = 0,	y = x − 5,	x = 2
15.	y = x3	− 2,	x = 0,	y = x − 6,	x = 2
16.	y = x3	+ 3,	x = 0,	y = x + 7,	x = −2
17.	y = x3	+ 2,	x = 0,	y = x + 6,	x = −2
18.	y = x3	+ 1,	x = 0,	y = x + 5,	x = −2

НГАВТ - Стр 31 из 45

19.		y = x3 − 1,	x = 0,	y = x + 3,	x = −2
20.		y = x3 − 2,	x = 0,	y = x + 2,	x = −3
		V. Вычислить объем тела, образованного вращением вокруг оси Ox кривой
L .
1.	x2 − y = 0, x = −1, y = 0				2.	x2 + y = 0, x = 0, y = −1
3.	x2 + 2 y = 0, x = 1, y = 0				4.	x2 − y = 0, x = 0, y = 1
5.	x2 − y = 0, x = 1, y = 0				6.	x − y2 = 0, x = 1, y = 0
7.	x − y2 = 0, x = 0, y = −1				8.	x + y2 = 0, x = −1, y = 0
9.		x − y2 = 0,	x = 0,	y = 1	10.		x + y2 = 0,	x = 0,	y = 1
11.		y = −4x3 ,	x = 0,	y = 4	12.		y = −4x3 ,	x = 1,	y = 0
13.		y = 4x3 ,	x = 0, y = 4		14.		y = 4x3 ,	x = 1,	y = 0
15.		y = 1 + 8x3 , x = 0,		y = 9	16.		y = 4x3 ,	x = 0,	y = −4
17.		y = −4x3 ,	x = −1,	y = 0	18.		y = −4x3 ,	x = 0,	y = −4
19.		y = 4x3 ,	x = −1,	y = 0	20.		y = 1 + 8x3 , x = −1 / 2, y = 1

КОНТРОЛЬНАЯ РАБОТА № 5

I. Изменить порядок интегрирования в двойном интеграле. Сделать чертеж области интегрирования.

	0	−2 x+6		1	−8 y3
1.	ò dx ò f ( x, y)dy		2.	òdy ò f ( x, y)dy
	−1	−8 x2		0	−4 y−4
	1	4 x+4		0	8 y3
3.	òdx ò f ( x, y)dy		4.	ò dy ò f ( x, y)dy
	0	8 x3		−1	2 y−6
	0	8 x3		1	2 y+6
5.	ò dx ò f ( x, y)dy		6.	òdy ò f ( x, y)dy
	−1	4 x−4		0	8 y3
	1	−8 x3		0	−4 y+4
7.	òdx ò f ( x, y)dy		8.	ò dy ò f ( x, y)dy

−2 x−6

−1

−8 y3

1	−8 x3
9. òdx ò f ( x, y)dy
0	−4 x−4

	3		4 x − x 2
11.	òdx				ò f ( x, y)dy
	1	0
	5	0
13.	òdx				ò f ( x, y)dy
	3	−			8 x − x 2
	−1
	−1			−4 x − x 2
15.	òdx				ò f ( x, y)dy
	− 3	0
	−2	0
17.	òdx				ò f ( x, y)dy
	−4	−			−6 x− x2

	6		8 x−x2
19.	òdx				ò f ( x, y)dy
	2	0

НГАВТ - Стр 32 из 45

08 y3

10.ò dy ò f ( x, y)dy

	−1	4 y−4
	−1
	−1			−6 y− y2
12.	òdy					ò f ( x, y)dy
	−5		0
	−1		0
14.	òdy					ò f ( x, y)dy
	−3	−				−4 y− y2

	7		8 y− y2
16.	òdy					ò f ( x, y)dy
	1		0
	3		0
18.	òdy					ò f ( x, y)dy
	1	−			4 y− y2
	4		0
20.	òdy					ò f ( x, y)dy
	2	−			6 y− y2

II. А. Вычислить объем тела, ограниченного заданными поверхностями. Сде- лать схематический чертеж.

1.	x2 + y2 = 4,		y + 2z − 4 = 0, z = 0
2.	x2 + y2 = 1, y + 2z + 2 = 0, z = 0
3.	x2 + y2 = 4,		y − 2z − 4 = 0, z = 0
4.	x2 + y2 = 1, y − 2z − 2 = 0, z = 0
5.	x2 + y2	= 9,	y + 2z − 6 = 0, z = 0
6.	x2 + y2	= 4,	y − 2x − 4 = 0, z = 0
7.	x2 + y2	= 1, y − 2z + 2 = 0, z = 0
8.	x2 + y2 = 4, y + 2z + 4 = 0, z = 0
9.	x2 + y2	= 1, y + 2z − 2 = 0, z = 0
10.	x2 + y2 = 9,		y − 2x + 6 = 0, z = 0

Б. Выполнить следующие задания, сделав схематический чертеж.

1. Найти массу однородного тела, ограниченного поверхностями

x2 + y = 3, 2 y − z = 0, z = 0 .

НГАВТ - Стр 33 из 45

2.	Найти	массу	однородного	тела,	ограниченного	поверхностями
x − y − z = 0, y = 0, z = 0 .
3.	Найти	массу	однородного	тела,	ограниченного	поверхностями
x2 + y − 4 = 0, y − 2z = 0, z = 0 .
4.	Найти	массу	однородного	тела,	ограниченного	поверхностями
x − y + z = 0, x = 0, z = 0 .
5.	Найти момент инерции относительно оси Oz однородного тела, ограни-
ченного поверхностями			x + y − 1 = 0, x + y − 1 = 0, x = 0, z = 0, z − 2 = 0 .
6.	Найти	массу	однородного	тела,	ограниченного	поверхностями
x2 + y − 2 = 0, 3 y − 2z = 0, z = 0 .
7.	Найти	массу	однородного	тела,	ограниченного	поверхностями
3 y + z = 0, x − 2 = 0, z = 0 .
8.	Найти	массу	однородного	тела,	ограниченного	поверхностями
x2 + y − 1 = 0, y − 2z = 0, z = 0 .
9.	Найти	массу	однородного	тела,	ограниченного	поверхностями
x − 3 y = 0, 2x − z = 0, y − 2 = 0, z = 0 .

11. Найти момент инерции относительно оси Oz однородного тела, ограни- ченного поверхностями x + y = 0, x − y = 0, x − 1 = 0, z = 0, z = 3 .

III. А. Требуется: 1) найти поток векторного поля a через замкнутую поверхность σ = σ 1 + σ 2 (выбирается внешняя нормаль к σ ); 2) вычислить

циркуляцию векторного поля a по контуру Г , образованному пересечением поверхностей σ 1 и σ 2 (направление обхода должно быть выбрано так, чтобы

область, ограниченная контуром Г , находилась слева); 3) проверить

правильность вычисленных значений потока и циркуляции с помощью формул Остроградского и Стокса; 4) дать заключение о наличии источников или стоков внутри области, ограниченной поверхностью σ ; 5) сделать схематический чертеж поверхности σ .

1.	a = (3 y − 5x)i + (6x + 5 y) y + (4z − xy + 4)k,
	σ 1 : x2 + y2 = (z + 1)2 , σ 2 : z = 1.
2.	a = ( x − y)i + (2x + y) y + ( x2 + 2z + 4)k,
	σ 1 : x2 + y2 = (z + 2)2 , σ 2 : z = 4.
3.	a = (3x + 2 y)i + (5x − 2 y) y + (3z − y2 − 3)k,
	σ 1 : x2 + y2 = (z − 1)2 , σ 2 : z = 3.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 159 10 11 12 13 14 15 > Следующая >>>