Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ярославский Государственный Технический Университет

Предмет:

Высшая математика

Файл:

Математика высшая

.pdf

Скачиваний:

Добавлен:

15.05.2015

Размер:

1.35 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 157 8 9 10 11 12 13 14 15 > Следующая >>>

НГАВТ - Стр 4 из 45

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНЫМ РАБОТАМ

КОНТРОЛЬНАЯ РАБОТА № 4

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Основные теоретические сведения

1. Неопределенным интегралом от функции f (x) называется выражение вида ò f ( x)dx = F ( x) + C , если F ′(x) = f (x) . Функция F ( x) F(x)

называется первообразной для заданной функции f (x) .

При интегрировании наиболее часто используются следующие методы.
1)	Если ò f ( x)dx = F ( x) + C , то
ò	f (ax)dx =	1	F (ax ) + C;	ò f ( x + b)dx = F ( x + b) + C ,	(1)

		a
где a и b — некоторые постоянные.
2)	Подведение под знак дифференциала:
			′		(2)
	ò f (ϕ ( x))ϕ ( x)dx =ò f (ϕ ( x))d (ϕ ( x)),
так как ϕ ′(x)dx = dϕ ( x) .
3)	Формула интегрирования по частям:
			ò udv = uv −ò vdu.		(3)

Обычно выражение dv выбирается так, чтобы его интегрирование не вызы- вало особых затруднений. За u , как правило, принимается такая функция, диф- ференцирование которой приводит к ее упрощению. К классам функций,

интегрируемых	по частям, относятся, в частности, функции вида P( x)e ax ,
P( x) sin ax ,	P( x) cos ax , P( x) ln x , P( x) arcsin x , P ( x)arctgx , где

P ( x) - многочлен от х.

4) Интегрирование рациональных дробей, т. с. отношений двух многочленов

Pk ( x) и Qn ( x) (соответственно k -й и n -й степени): R( x) = Pk ( x) / Qn ( x) ,

НГАВТ - Стр 5 из 45

сводится	к разложению подынтегральной функции R( x)						на элементарные,
всегда интегрируемые дроби вида
		A			Mx + N
			,			,	(4)
		( x - a)l	,	( x 2	+ px + q)m	,	(4)
где l и	m - целые положительные числа, а трехчлен x 2						+ px + q не имеет

действительных корней. При этом в случае неправильной дроби ( k ³ n ) должна быть предварительно выделена целая часть.

5) Интегрирование методом замены переменной (способом подстановки)

является одним из эффективных приемов интегрирования. Его сущность состоит в переходе от переменной x к новой переменной t : x = ϕ (t) . Наиболее целесообразная для данного интеграла замена переменной, т. е. выбор функции ϕ (t) , не всегда очевидна. Однако для некоторых часто встречающихся классов функций можно указать такие стандартные подстановки:

ax + b

= t;

ò Rç x,

ax + d

÷ dx,

ax + d

ò R(x,

)dx,

- x 2

x = a × sin t;

ò R(x,

)dx,

+ x 2

x = a × tgt;

ò R(x,

)dx,

x 2 - a2

x =

sin t

где R - символ рациональной функции.

2. Формула Ньютона — Лейбница для вычисления определенного интеграла

имеет вид

b	b
ò f ( x)dx = F ( x)	= F (b) - F (a),	(5)
ò f ( x)dx = F ( x)	= F (b) - F (a),	(5)
a	a

′
если F ( x) = f ( x) и первообразная F ( x) непрерывна на отрезке [a, b] .
Определенный интеграл численно равен площади криволинейной трапеции,
ограниченной прямыми x = a, x = b,	y = 0 и частью графика	функции
y = f ( x) , взятой со знаком плюс, если	f ( x) ³ 0 , и со знаком минус, если
f ( x) £ 0 .
3. Если интервал интегрирования [a, b] не ограничен (например,		b = ¥ )

НГАВТ - Стр 6 из 45

или функция f ( x) не	ограничена в окрестности одного из пределов
интегрирования (например, при x = b ), то по определению полагают
+∞	b
ò f ( x)dx = blim→∞ ò f ( x)dx,		(6)
a	a
и	b−a
b	b−a
ò f ( x)dx = lima→0 ò f ( x)dx,		(7)
a	a

Интегралы в левых частях равенств (6) н (7) называются несобственными интег- ралами. Несобственный интеграл называется сходящимся, если существует конеч- ный предел в правой части равенств (б) и (7). Если же предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.

4. Пусть криволинейная трапеция, ограниченная прямыми

x = a, x = b,

y = 0

и частью графика кривой

y = f ( x) , вращается вокруг оси Ox . Тогда

объем полученного при этом тела вращения вычисляется по формуле

V = π ò y2dx =π ò( f ( x))2 dx,

(8)

Пример 1. Найти ò

(2x - 3)2

Решение. Так как ò

= -

+ C , то, используя формулы (1), получим

x 2

d(2x)

d(2x - 3)

= -

+ C.

(2x -

(2x - 3)

2(2x - 3)

(2x - 3)

Проверка:

′

- 2

+ C ÷

= -

2(2x - 3)

2 è 2x - 3 ø

(2x -

(2x - 3)

Пример 2. Найти òcos xe sin x dx .

Решение. Так как cos xdx = d(sin x) , то по формуле (2) находим

òcos xe sin x dx = ò e sin x d(sin x) = esin x

+ C.

НГАВТ - Стр 7 из 45

Пример 3. Найти ò x cos 2xdx .

Решение. Применим метод интегрирования по частям. Положим u = x, dv = cos 2xdx ; тогда du = dx, v = 12 sin 2x . Используя формулу (3), имеем

òx cos 2xdx = 12 x sin 2x - 12 òsin 2xdx =

=12 x sin 2x + 14 cos 2x + C.

3x 2 - 7 x + 10

Пример 4. Найти ò ( x 2 + 4)( x - 2) dx .

Решение. Подынтегральная рациональная дробь является правильной и раз- лагается на элементарные дроби вида (4):

3x 2 - 7 x + 10	=	Ax + B		+	C	.
( x 2 + 4)( x - 2)		x 2	+ 4		x - 2

Освобождаясь от знаменателей в обеих частях этого равенства и приравнивая числители, получаем тождество для вычисления неопределенных коэффициентов

А, В и С:

3x 2 - 7 x + 10 º Ax( x - 2) + B( x - 2) + Cx 2 + 4C

Составим систему трех уравнений с тремя неизвестными. Одно уравнение полу-

чим, полагая x = 2 (корень знаменателя подынтегральной функции). Два других получим, приравнивая коэффициенты при одинаковых степенях x в обеих частях

тождества, например при x 2 и

x0 :

x = 2 : 8 = 4C + 4C,

x 2

3 = A + C,

x0 : 10 = -2B + 4C.

Решение этой системы дает:

A = 2, B = −3, C = 1 . Таким образом,

3x 2 - 7 x + 10

æ 2x - 3

1 ö

dx = òç

÷dx =

( x

+ 4)( x - 2)

+ 4

x - 2

è x

= ò

2xdx

- 3ò

+ ò

= ln( x 2

+ 4) -

arctg

+ ln

x - 2

+ C.

+ 4

x -

- 1

Пример 5. Вычислить определенный интеграл

ò4

x +

НГАВТ - Стр 8 из 45

Решение. Применим метод замены переменной; положим 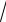x = t , откуда dx = 2tdt . Найдем пределы интегрирования по переменной t : при x = 4 имеем

t = 2 ,

а при

x = 9

имеем

t = 3 . Переходя в исходном интеграле к новой

переменной t

и применяя формулу Ньютона — Лейбница (5), получаем

− 1

t − 1

dx = ò

2tdt = (t 2 − 4t + 4 ln

t + 1

)

x + 1

t + 1

= (9 − 12 + 4 ln 4) − (4 − 8 + 4 ln 3) = 2,15.

Пример 6. Вычислить несобственный интеграл или установить его расходи-

∞

π 4

мость:

1) òe

; 2)

ò0

x ln x

sin 2

Решение. 1) Первый интеграл является несобственным интегралом с бес- конечным верхним пределом интегрирования. Согласно определению (6), имеем

∞	dx		b	dx
ò		= lim	ò		= lim(ln	ln x	)

	x ln x			x ln x
e		b→∞ a			b→∞

l	= lim(ln	ln b	) − 0 = ∞.

e	b→∞

Следовательно, данный интеграл расходится.

2) Второй интеграл является несобственным интегралом от неограниченной

функции;

f ( x) =

терпит бесконечный разрыв в нижнем пределе при

sin

x = 0. Согласно определению (7), получаем

π 4

= lim

= lim(tg x)

= 1

− lim(tg ε ) = 1,

sin

ε →

ε →0

т. e. этот несобственный интеграл сходится.

Пример 7. Вычислять площадь плоской фигуры, ограниченной кривыми y1 = sin x + 2, y2 = −1, x = 0, x = π (рис. 10).

-1

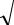
НГАВТ - Стр 9 из 45

			Рис. 10
	π		π
Решение.	S = ò( y1 − y2 )dx = ò(sin x + 2 + 1)dx = 2 + 3π .
	0		0
Пртер 8. Вычислить объем тела, образованного вращением вокруг оси Ox
кривой y =
	4x − x 2	, y = 0, x = 2 (0 ≤ x ≤ 2) .
Решение. Объем полученного тела вращения найдем по формуле (8):
	2		2	16π
	V = π ò y2dx = π ò(4x − x 2 )dx =				.
				3
	0		0

КОНТРОЛЬНАЯ РАБОТА № 5

КРАТНЫЕ ИНТЕГРАЛЫ.

ЭЛЕМЕНТЫ ТЕОРИИ ВЕКТОРНЫХ ПОЛЕЙ

Основные теоретические сведения

1. Вычисление двойного интеграла от функции f ( x, y) , области D , сводится к вычислению двукратного интеграла вида

òò	b	f2 ( x )
òò	f ( x, y)dxdy = ò dx	ò f ( x, y)dy,
D	a	f1 ( x )

определенной в

(1)

если область	D определяется условиями			a ≤ x ≤ b, f1 ( x) ≤ y ≤ f2 ( x),	или
вида
	òò	d	ϕ 2	( y)
	òò	f ( x, y)dxdy = ò dx	ò f ( x, y)dx,		(2)
	D	c	ϕ1 ( y)
если область	D	определяется условиями c ≤ y ≤ d, ϕ1 ( y) ≤ x ≤ ϕ 2 ( y) .

Переход от равенства (1) к (2) иди обратно называется изменением порядка интегрирования. Значение двойного интеграла не зависит от порядка

НГАВТ - Стр 10 из 45

интегрирования.

2. Вычисление тройного интеграла от функции f ( x, y, z) , определенной в области V , сводится к вычислению интеграла вида

òòò	f ( x, y, z) = òò dxdy		ψ 2 ( x , y)
òòò	f ( x, y, z) = òò dxdy		ò f ( x, y, z)dz,		(3)
V		Dxy	ψ 1 ( x, y)
где Dxy - проекция области		V	на	плоскость	xOy, z = ψ 1 ( x, y) и
z = ψ 2 ( x, y) —	уравнения	поверхностей,		ограничивающих область V

соответственно снизу и сверху. В тройном интеграле, так же как и в двойном, порядок интегрирования может быть изменен.

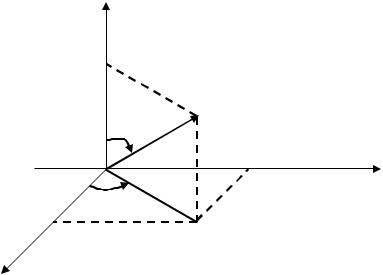
3. Наряду с прямоугольной системой координат пространстве могут быть введены цилиндрическая и сферическая системы координат (рис. 11).

Прямоугольные координаты (x; y; z) точки M связаны с ее цилиндрическими (ρ;ϕ; z) и сферическими (r;θ;ϕ ) координатами соотношениями

ìx = ρ cosϕ ,

ïí y = ρ sinϕ ,

ïî z = z;

ìx = r sinθ cosϕ ,
ï	(4)
í y = r sinθ sinϕ ,	(4)
ï
î z = r cosθ .

		θ	M
		θ
0		r
0		ψ	Y
	ϕ	ψ	Y
	ϕ		x

Рис. 11

Тройной интеграл записывается в виде

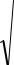
НГАВТ - Стр 11 из 45

òòò f ( x, y, z)dxdydz =

ì òòò

=ïí V

ïòòò

î V

f (ρ ,ϕ , z)ρ dϕ dρ dz - в цилиндриче ской системе ;	(5)
f (r,θ ,ϕ )r 2 sinθ dϕ dθ dr - в сферическо й системе .

4. Вычисление криволинейного интеграла по координатам от функций, опре- деленных на кривой Г , сводится к вычислению определенного интеграла вида

ò P( x, y, z)dx + Q( x, y, z)dy + R( x, y, z)dz =

β		(6)
¢	¢	(6)
= ò P( x(t), y(t), z(t)) x (t)dt + Q( x(t), y(t), z(t)) y (t)dt +
α
¢
+ R( x(t), y(t), z(t))z (t)dt,
если кривая Г задана параметрически:	x = x(t), y = y(t), z = z(t) и	t = α

соответствует начальной точке кривой Г , а t = β — ее конечной точке.

5.Вычисление поверхностного интеграла от функции F ( x, y, z) ,

определенной на двусторонней поверхности σ , сводится к вычислению двойного интеграла, например, вида

òò F ( x, y, z)dσ = òò F ( x, y,

f ( x, y))

dxdy

(7)

cos γ

Dxy

z = f (x, y) , однозначно проециру-

если поверхность σ , заданная уравнением

ется на плоскость xOy в область

Dxy .

Здесь γ - угол между единичным

вектором нормали n к поверхности σ и осью Oz .

¶f

¶x

¶y

- k

n = ±

(8)

¶f

æ ¶f

¶x

+ ç

+ 1

¶y ø

Требуемая условиями задачи сторона поверхности а определяется выбором соот-

НГАВТ - Стр 12 из 45

ветствующего знака в формуле (8).

6. С помощью тронных интегралов можно вычислить: а) объем V тела и его массу M :

V = òòò dxdydz , M = òòò μ( x, y, z)dxdydz ,

V V

где μ - объемная плотность распределения массы;

б) момент инерции однородного тела относительно, например, оси Oz :

I z = òòò ( x 2 + y2 )dxdydz .

7.Векторным полем a(M ) называется векторная функция точки M вместе

собластью ее определения:

a(M ) = P( x, y, z)i + Q( x, y, z) j + R( x, y, z)k.

Векторное поле a(M ) характеризуется скалярной величиной — дивергенцией

¶P

¶Q

¶R

div a

(9)

¶x

¶y

¶z

и векторной величиной — ротором:

rota =

¶x

¶y

¶z

(10)

æ ¶R

¶Q ör

æ ¶P

¶R ö r

æ ¶Q

¶P ö r

= ç

÷i +

÷ j

+ ç

÷k .

¶z

è ¶z

¶x ø

¶x

è ¶y

¶y ø

8. Потоком векторного поля a(M ) через поверхность σ называется поверх

ностный интеграл

П = òò (a, n)dσ ,

(11)

НГАВТ - Стр 13 из 45

где n - единичный вектор нормали к выбранной стороне поверхности σ , а (a, n) - скалярное произведение векторов a и n .

9. Циркуляцией векторного поля	a = P(x, y, z)i + Q( x, y, z) j + R( x, y, z)k no
замкнутой кривой Г называется криволинейный интеграл
Ц = ò Pdx + Qdy + Rdz = ò ardrr,		(12)
Г	Г

где dr = dxi + dyj + dzk .

10. Формула Остроградского устанавливает связь между потоком векторного поля a через замкнутую поверхность σ и дивергенцией поля:

r r	r
òò (a, n)dσ = òòò divadV ,		(13)
σ	V

где V - объем, ограниченный поверхностью σ .

11. Формула Стокса устанавливает связь между циркуляцией векторного

поля a и его ротором:
	r r
ò Pdx + Qdy + Rdz = òò (rota, n)dσ ,		(14)
Г	σ

где σ — поверхность, ограниченная замкнутым контуром Г , а n — единичный вектор нормали к этой поверхности. Направление нормали должно быть со- гласовано с направлением обхода контура Г .

Пример 1. Изменить порядок интегрирования в двойном интеграле

2 x

I = ò dx ò f ( x, y)dy.


0	−2			x
Решение. Зная пределы интегрирования, найдем границы области интег-
рирования D : x = 0, x = 1, y = 2			, y = −2
		x			x	и построим их (рис.		12).
Область D располагается в полосе		0 ≤ x ≤ 1			и	ограничена снизу	и сверху
соответствующими ветвями параболы		y2 = 4x .			y )				x )
Найдем новые пределы внешнего (по						и внутреннего	(по
интегрирования. Так как область D проецируется на ось Oy в отрезок							AB ,		то
пределами внешнего интегрирования являются ординаты точек A и							B ,	т.	е.

<<< < Предыдущая 1 2 3 4 5 67 / 157 8 9 10 11 12 13 14 15 > Следующая >>>