Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ярославский Государственный Технический Университет

Предмет:

Высшая математика

Файл:

Математика высшая

.pdf

Скачиваний:

Добавлен:

15.05.2015

Размер:

1.35 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1512 13 14 15 > Следующая >>>

= − y	dy	= −dx ln y = − x + ln C ln	y	= − x y C e	− x	общее
					—
	y		C

решение однородного уравнения.

Применяем далее метод вариации произвольной постоянной C . Общее


решение неоднородного уравнения будем искать						в	виде	y = C ( x )e − x ;
y′ = C ′( x )e − x − C ( x )e − x . Подставив			значения			y и	y′	в неоднородное
уравнение, получим
xC ′( x )e − x − xC ( x )e − x + xC ( x )e − x = e − x xe − x C ( x ) = e − x .
Так как e − x ≠ 0 , то
xC ′( x ) = 1 x	dC ( x )	= 1 dC ( x ) =		dx	C ( x ) = ln x + C .
xC ′( x ) = 1 x		= 1 dC ( x ) =			C ( x ) = ln x + C .
	dx			x

Подставив это значение C ( x ) в общее решение неоднородного уравнения, полу-

чим

y = (ln x + C )e − x

— общее решение неоднородного уравнения.

Для нахождения частного решения подставим значения

x = 1, y = 2

в об-

щее решение:

y(1) = 2 2 = (0 + C ) 1 C = 2 . Значит,

y = (ln x + C )e − x

— частное решение неоднородного уравнения.

Пример 2. Найтн общее решение уравнения 2 xy′′′ =

y′′

и частное решение,

удовлетворяющее начальным условиям y(1) = −1; y′(1) = 0; y′′(1) = 1 .

Решение.

Пусть

y′′ = z .

Имеем 2 xz ′ − z = 0 2 x

= z

ln z =

ln x + ln C

1 z = C1

x . Но z = y′′ y′′ = C1

y′ = C1

x 3 2

+ C 2 ; y′ =

y =

x 5 2

C1 x x + C 2

+ C 2 x + C

3 .

5 2

3 2

Следовательно,

y =

C1 x 2

x + C 2 x + C 3 — общее решение дифференци-

ального уравнения.

Чтобы найти частное решение, подставим в выражения для y, y′, y′′ значение x = 1 :

y(1) = −1

+ C

= −1;

y′(1) = 0

+ C

= 0;

y′′(1) = 1 C1

= 1.

Из

системы уравнений C 2 + C 3

; C 2

= −

находим C 2

= −

;

C 3 = −

. Значит, искомое частное решение имеет вид

y =

x 2 −

−

x −

Пример 3. Найти общее решение уравнения

y′′ + 4 y′ + 13 y = 5 sin 2 x

частное

решение, удовлетворяющее

начальным

условиям

; y′

при x = 0 .

y′′ + 4 y′ + 13 y = 0 .

Решение. Рассмотрим однородное уравнение

Соответствующее характеристическое уравнение имеет вид

k 2 + 4k + 13 = 0 ,

откуда

k1 = −2 − 3i, k2

= −2 + 3i .

Следовательно,

Y = e −2 x (C1 cos 3 x +

+ C 2 sin 3 x ) общее решение однородного уравнения.

Частное решение

неоднородного

уравнения

будем

искать

виде

y* = A cos 2 x + B sin 2 x . Имеем

y*′ = −2 A sin 2 x + 2 B cos 2 x , y*″ = −4 A cos 2 x − 4 B sin 2 x .

Подставим эти выражения в неоднородное уравнение

− 4 A cos 2 x − 4 B sin 2 x − 8 A sin 2 x + 8 B cos 2 x + 13 A cos 2 x +

+ 13 B sin 2 x = 5 sin 2 x;

(9 A + 8 B ) cos 2 x + ( −8 A + 9 B ) sin 2 x = 5 sin 2 x

иполучим систему для вычисления коэффициентов A и B :

	9 A + 8 B = 0	A = −	8

			29
			29

			9
− 8 A + 9 B = 5		B =
− 8 A + 9 B = 5		B =	29
			29

Итак, частное решение неоднородного уравнения имеет вид

y* = −	8	cos 2 x +	9	sin 2 x ,

29		29

а общее решение неоднородного уравнения — вид

y = e	− 2 x (C		cos 3 x + C		sin 3 x ) −	8	cos 2 x +	9	sin 2 x.
		1		2
					29		29

Найдем частное решение, удовлетворяющее заданным начальным условиям:

							y		=	2	С							−				8	=	2			С					=	10		;
							y	0	=		С					1		−					=				С			1		=			;
								0	29							1			29				29							1		29
									29										29				29									29
	y′ = −2 x		−2 x (C		1		cos 3 x + C					2	sin 3 x ) + e −2 x													( −3C				1		sin 3 x + 3C							2	cos 3 x ) +
					1							2																		1									2
+	16	sin 2 x +		18		cos 2 x;					y′ =					1						− 2C					+	3C				+		18		=	1		C			=	1	.
+		sin 2 x +				cos 2 x;					y′ =											− 2C			1		+	3C			2	+				=			C		2	=		.
29			29													29									1						2	29			29						2	29
29			29													29																29			29							29
	Искомое частное решение таково:
						10									1												8								9
		y = e − 2 x							cos 3 x +										sin 3 x −										cos 2 x +									sin 2 x.
		y = e − 2 x							cos 3 x +										sin 3 x −										cos 2 x +									sin 2 x.
						29									29												29								29
	Пример 4. Найти общее решение системы
												dx					1				= x1 − 3 x2 ,
																	1
															dt
															dt
														dx 2						= x			2 − 3 x1 .
																				= x			2 − 3 x1 .
												dt

Решение. Перепишем систему в виде


		dx	1		= x1 − 3 x		,

		dt				2

	dx 2			= −3 x1 + x			2 .

dt
Рассмотрим характеристическое уравнение:

1 − λ

− 3

= 0

(1 − λ ) 2

− 9 = 0 1 − λ = ±3 λ = −2; λ

= 4.

− 3

1 − λ

Подставим найденные значения корней характеристического уравнения в

систему линейных алгебраических уравнений относительно

p1 , p2 .

Для λ = −2 имеем

(1 +

2) p

− 3 p

= 0

− 3 p

= 0

− p

= 0

− 3 p1 + (1 + 2) p2 = 0

− 3 p1 + 3 p2 = 0

p1 − p2 = 0

(второе уравнение есть следствие первого). Возьмем,

например,

= k ; тогда

p2 = −k . Полагая k = 1 ,

найдем

p1 = 1; p2 = −1 . Итак, для λ = −2 получим

x11 = e −2 t ; x 21 = e −2 t .

Для λ = 4 имеем

(1 −

4) p

− 3 p

= 0

− 3 p

= 0

− 3 p1

+ (1 − 4) p2 = 0

− 3 p1 − 3 p2

p1 +

(второе уравнение есть следствие первого). Возьмем, например,

p2 = −k . Полагая k = 1 , найдем p1 = 1 ; p2 = −1 . Итак, для

x12 = e 4 t ; x 22 = −e 4 t .

Фундаментальная система решений:

для λ = −2 : x11 = e −2 t ; x21 = e −2 t ,

для λ = 4 : x12 = e 4 t ; x22 = −e 4 t .

Следовательно, общее решение системы имеет вид

p2 = 0

p1 = k ; тогда λ = 4 получим

x1 = С1 e −2 t + С2 e 4 t , x2 = С1 e −2 t − С2 e 4 t

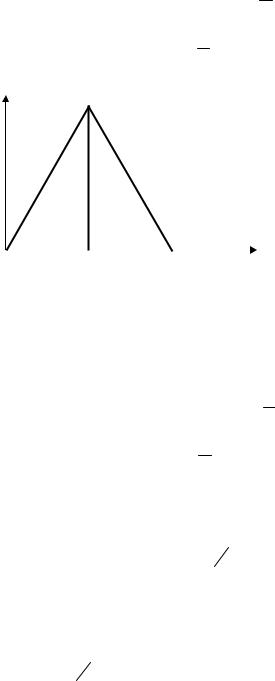
Пример 5. Дана струна, закрепленная на концах x = 0, x = l . Пусть в

начальный момент времени форма струны имеет вид ломаной OAB , изображенной на рис. 15. Найти форму струны для любого момента времени, если

2αx,

ψ ( x ) =

2α ( l − x ),

0 ≤ x ≤ l ,

l ≤ x ≤ l . 2

l/2

Рис. 15

Решение. Из рисунка и условия задачи имеем

	2h		x,

		l
ψ ( x ) =
		2h	( l − x ),

		l

0 ≤ x ≤ l ,

l ≤ x ≤ l . 2

Находим

2 l

kπx

∫

ϕ ( x ) sin

dx =

∫

x sin

dx +

l 2

kπx

+ ∫( l − x ) sin

dx .

Интеграл

∫ x sin

kπx

берем по частям; u = x, dv = sin

kπx

dx , откуда

du = dx , v = −

cos

kπx

следовательно;

kπ

∫ x sin

kπx

dx = −

x cos

kπx

∫

cos

kπx

dx =

kπ

= −

x cos

kπx

l 2

sin

kπx

kπ

2π 2

Итак,

kπx

∫

x sin

sin

dx −

x sin

2 ∫

l 2 ∫

В результате получим ak

sin

kπ

. Далее, находим

kπx

4α

kπx

ψ ( x ) sin

dx =

x sin

dx +

kπα ∫

4α

kπx

4α

kπx

∫( l − x )

sin

dx =

∫ x sin

dx +

kπα

4αl

kπx

4α

kπx

∫sin

dx −

∫ x sin

dx .

kπα

Окончательно получим bk =

8αl 2

sin

kπ

π α

Таким образом, искомая функция имеет вид

∞

kπα t αl

kπα t

kπ

kπx

u( x, t ) =

∑

cos

3 sin

sin

k =1

КОНТРОЛЬНАЯ РАБОТА № 8

ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Основные теоретические сведения

1. При классическом определенна вероятность события A определяется

соотношением P ( A) = n , где m — число элементарных исходов испытания,

благопринятствующнх наступлению события A , а n — общее число возможных элементарных исходов испытания. Предполагается, что элементарные исходы

единственно возможны и равновозможны. Относительная частота события A

есть w( A) = n , где n — число испытаний, в которых событие A наступило, а

n — общее число произведенных испытании.

При статистическом определении в качестве вероятности события принимают его относительную частоту.

2.Схема испытаний Бернулли (повторение опытов). Вероятность того, что

вn независимых испытаниях, в каждом из которых вероятность появления

события равна p (0 < p < 1) , событие наступит ровно k			раз (безразлично, в
какой последовательности), есть
P ( k ) = C k p k q n − k , где q = 1		− p	(1)
n	n

Вероятность того, что событие наступит:

а) менее k раз: Pn (0) + Pn (1) + ... + Pn ( k − 1) ,

б) более k раз: Pn ( k + 1) + Pn ( k + 2) + ... + Pn ( n) ,

в) не менее k раз: Pn ( k ) + Pn ( k + 1) + ... + Pn ( n) ,

г) не более k раз: Pn (0) + Pn (1) + ... + Pn ( k ) .

3. Если число испытаний n велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях пользуются предельными теоремами Лапласа.

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1) ,

событие наступит ровно k раз (безразлично, в какой последовательности), выражается приближенным равенством

Pn ( k ) ≈

ϕ ( x ),

(2)

npq

где

ϕ ( x ) =

e − x 2

2 ; x =

− np

Функция

ϕ ( x ) — четная, т.

е.

2π

npq

ϕ ( − x ) = ϕ ( x ) . При x > 5 можно считать, что ϕ ( x ) = 0 .

Интугральная теорема Лапласа. Вероятность TОГО, ЧТО В n независимых

испытаниях, в

каждом из

которых

вероятность

появления

события равна

p (0 < p < 1) , событие наступит не менее k1

раз и не более k2

раз, выражается

приближенным равенством

P ( k1 ; k2 ) ≈ Ф( x2 ) − Ф( x1 ),

(3)

Ф( x ) =

− t 2

2 dt

k1 − np

где

функция Лапласа;

—

;

2π ∫0

npq

x 2

k2 − np

. При x > 5

полагают ϕ ( x ) = 0,5 . Функция Лапласа—четная,

npq

т. е. Ф( − x ) = Ф( x ) .

4. Нормальным распределением называют распределение вероятностей

непрерывной случайной величины

X , плотность распределения которого имеет

вид

( x − m ) 2

f ( x ) =

2α 2

σ 2π

где

m — математическое ожидание, а σ - среднее квадратическое отклонение

величины X .

Вероятность

того,

что

x примет значение,

принадлежащее интервалу

(α , β ) , составляет

β − m

− m

P (α < x < β ) = Ф

−

(4)

где Ф( x ) — функция Лапласа.

Вероятность того, что абсолютная величина отклонения меньше положитель-

ного числа σ , выражается равенством

P (

x − m

< σ ) = 2Ф(δ σ ).

(5)

5. Если линия регрессии

на

X — прямая, то корреляцию называют

линейной. Выборочное уравнение прямой линии регрессии Y на X имеет вид

−

= r

σ y

( x −

(6)

σ x

∑nxy xy − n

где B

nσ xσ y

Если данные наблюдения над признаками

и Y

заданы в виде

корреляционной

таблицы

с равноотстоящими

вариантами,

то целесообразно

− C

, v j

y j

− C 2

перейти к условным вариантам

, где C1 — ложный

нуль вариант X

(в качестве его выгодно принять варианту, расположенную

примерно в центре вариационного ряда и имеющую наибольшую частоту); h1

—

шаг, т. е. разность между соседними

вариантами

X . Величины C 2 и

относятся к варианту Y . В этом случае выборочный коэффициент корреляции.

		∑nuv uv − n
r	=		u	v	(7)
		.
B		nσ uσ v

Величины u , v , σ u , σ v , могут быть найдены либо методом произведений, либо непосредственно по формулам

∑nu u

∑nv v

u =

; v =

u − ( u )

; σ

v − ( v )

; σ

Зная эти величины, можно определить входящие в уравнение регрессии значения по формулам

Пример 1. Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию нз 5 человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того,

что в делегацию войдут 2 женщины и 3 мужчины.

Решение. Число всех способов выбора 5 человек из 25 равно С253 , а число

способов выбора двух женщин из 5 равно					С52 . Каждая такая двойка может
сочетаться с каждой тройкой из 20			мужчин. Число таких троек равно С203 .
Искомая вероятность составляет
P =	C 2	С 3	=	380	≈ 0,215 .
	5	20
	C 5			1771
	C 5			1771
		25

Пример 2. Слово «лотос», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают одну за другой три буквы. Какова вероятность того, что при этом появится слово

«сто»?

Решение. Вероятность появления буквы «с» равна												1		. Вероятность появле-
												5
ния вслед за ней буквы «т» равна			1	, и, наконец, вероятность появления буквы

			4
«о» равна -	2	. Искомая вероятность P =			1		1		2	=	1		≈ 0,033 .
											30
3			5			4		3

Пример 3. Случайно встреченное лицо с вероятностью 0,2 может оказаться брюнетом, с вероятностью 0,3 — блондином, с вероятностью 0,4 — шатеном и с вероятностью 0,1 —рыжим. Каковая вероятность того, что среди пяти случайно встреченных лиц: а) не мевее четырех блондинов; б) два блондина н три шатена; в) хотя бы один рыжий?

Решение, а) Искомая вероятность составляет [см. формулу (1)]

P = P5 (4) + P5 (5) = C 54 (0,3) 4 (0,7 )1 + C 55 (0,3) 5 (0,7 ) 0 = 0,03078

б) Искомая вероятность

P= P5 ( 2) + P5 ( 3) = [C 52 (0,3) 2 (0,7 ) 3 ] [C 53 (0,4) 3 (0,6) 2 ] =

=0,3078 0,2304 ≈ 0,07.

в) Искомая вероятность

P = 1 − P5 (0) = 1 − C 50 (0,1) 0 (0,9) 4 = 1 − 0,6561 = 0,3439 .

Пример 4. Игральную кость подбрасывают 500 раз. Какова вероятность того,

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1512 13 14 15 > Следующая >>>