discr_math

Указанные классы эквивалентности обычно называют классами вы-

четов по модулю 5. Фактор-множество Z/ , которое мы обозна-

чим символом Z5 , содержит ровно пять элементов:

Z5 { [0], [1], [2], [3], [4] }.

Нетрудно заметить, что каждый из перечисленных классов эквива-

лентности однозначно задается любым своим элементом, например,

[1] [6] [ 9] и т.д. Кроме этого, указанные классы не пересекают-

ся, а их объединение представляет собой разбиение множества це-

лых чисел: Z [0] [1] [2] [3] [4].

Отметим, наконец, что каждый из перечисленных классов эквивалентности удобно рассматривать как множество целых чисел,

которые при делении на 5 имеют остатки, равные 0, 1, 2, 3 и 4 соот-

имеет следующий вид:

[a] { ,a km, , a 2m, a m, a, a m, a 2m, , a km, }.

10 В записи n 5k q остаток q {0,1, 2,3, 4}, а неполное частное k может быть отрицательным целым числом.

62

Важнейшее свойство любого отношения эквивалентности на

X состоит в том, что оно порождает соответствующее разбиение множества X .

Теорема 1.6. Любое отношение эквивалентности на X порождает разбиение множества X :

X [x].

x X

► 1) Сначала отметим, что для любого элемента x X выполняется условие x [x] и поэтому множество [x] Ø.

2) Поскольку x [x], множество {x} является подмножеством клас-

са эквивалентности {x} [x] и поэтому

X {x} [x].

x X x X

С другой стороны, любой класс эквивалентности [x] является под-

множеством множества X , значит, справедливо и обратное вложе-

ние: [x] X .

x X

3) Наконец, любые два класса эквивалентности [x]и [y] либо сов-

падают, либо имеют пустое пересечение. В самом деле, если пред-

положить, что [x] [y] Ø, то найдется элемент z X такой, что

z [x] [y], и, следовательно, z ~ x и z ~ y. В силу симметрич-

ности отношения, из z ~ x имеем x ~ z , а с учетом транзитивности

отношения, из x ~ z и z ~ y получим x ~ y . В результате для любо-

го элемента t y получим t ~ y ~ x, значит, t [x], и справедливо

63

вложение [y] [x]. Аналогичными рассуждениями можно обос-

новать обратное вложение [x] [y]. Таким образом, если

[x] [y] Ø, то [x] [y].◄

Предположим теперь, что уже имеется некоторое (фиксиро-

ванное) разбиение произвольного множества X :

Зададим отношение на X следующим образом: элементы x и y

находятся в отношении , если они оба принадлежат одному из

множеств Ai . Рефлексивность и симметричность этого отношения очевидна. Проверим транзитивность отношения . Предположим,

что пары (x, y) и (y,z) . Тогда найдутся множества Ai и Aj та-

x,z Ai , пара (x,z) , отношение транзитивно и является от-

ношением эквивалентности.

Рассуждения, которые мы сейчас провели, позволяют сфор-

мулировать следующую теорему.

Теорема 1.7. Любое разбиение множества X порождает соответст-

вующее отношение эквивалентности на этом множестве.

64

Теоремы 1.6 и 1.7 позволяют сделать вывод о существова-

нии биективного отображения между множеством всех отношений эквивалентности на X и множеством всех разбиений множества X .

Отношения порядка

В предыдущем разделе мы увидели, как на основе обычного отношения равенства между числами возникает понятие эквива-

лентности элементов произвольного множества. Точно так же чи-

словые неравенства могут служить основой для построения более

широкого класса отношений порядка.

Определение 1.46. Отношение на X называется предпорядком

(квазипорядком), если оно рефлексивно и транзитивно.

Определение 1.47. Отношение на X называется порядком, если оно рефлексивно, антисимметрично и транзитивно.

Пример 1.47. На множестве Z\{0} введем отношение x y , если число y является делителем числа x:

и y k2 z , то x k1k2 z nz ). Однако не является симметричным:

например, число 3 является делителем числа 6, но число 6 не являет-

ся делителем 3. Одновременно не является и антисимметричным,

поскольку 3 ( 1) 3 и 3 ( 1) ( 3) , но, конечно, 3 3.

65

Таким образом, указанное отношение делимости является предпо-

рядком.

Порядок называется линейным (или полным), если для лю-

какая-то пара несравнимых между собой элементов (т.е. обе пары

(x, y) и (y,x) не принадлежат ), порядок называется частичным.

Определение 1.48. Отношение на X называется строгим по-

рядком, если оно транзитивно и сильно антисимметрично.

Пример 1.48. Отношение на множестве действительных чисел R

является линейным порядком.

Пример 1.49. Отношение < на R является строгим линейным по-

рядком.

Пример 1.50. Отношение подчиненности на предприятии задает частичный строгий порядок. Несравнимыми по такому отношению являются сотрудники различных отделов.

Пример 1.51. Отношение вложения на булеане B(X) множества

X является частичным порядком. Пусть A, B и C - произвольные

все элементы булеана сравнимы между собой. Например, не срав-

(линейно) упорядоченным множеством. Для отношения порядка на

произвольном множестве часто используют символ 7, соответст-

венно для строгого порядка можно использовать символ 3 .

Любое упорядоченное множество можно представить в виде

понижающей диаграммы (диаграммы Хассе), в которой каждый эле-

мент множества изображается точкой на плоскости, причем, если y

накрывает x, то точку y располагают выше точки x и соединяют обе точки отрезком.

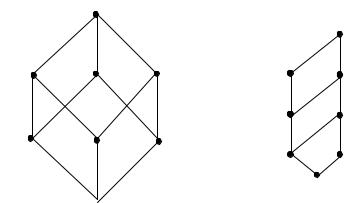
Пример 1.52. Для булеана множества X {a,b,c}, частично упоря-

доченного с помощью отношения вложения, диаграмма Хассе при-

ведена на рис. 1.22.

68

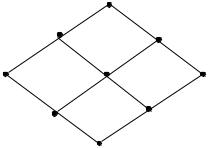
Пример 1.54. Пусть X {1,2,3} с естественным отношением ли-

нейного порядка на N. Частичному порядку по Парето на X X

соответствует диаграмма Хассе на рис. 1.24.

порядка . Так, например, буквы русского языка образуют алфавит с естественным линейным строгим порядком следования. Любой конечный набор записанных друг за другом символов называется

словом в алфавите. Пусть ai xi1xi2 xij xik есть некоторое сло-

во в алфавите. Количество букв слова (число k ) называется его дли-

ной. Множество всех слов алфавита обозначим символом A(X) и

будем считать, что A(X) содержит, помимо «обычных» слов, пус-

тое слово – длины 0 и не имеющее символов. На множестве A(X)

введем отношение порядка, используя заданный линейный порядок

пустые, а символы x1i и x2i связаны отношением линейного поряд-

ка : x1i x2i .

2) a2 a1 s, где s - некоторое непустое слово.

Такое отношение на множестве слов A(X) называется отношением

лексикографического порядка. Отметим без доказательства следую-

щий факт: если множество X является линейно упорядоченным,

то множество слов A(X), снабженное лексикографическим поряд-

ком, также будет линейно упорядоченным.

Пример 1.55. Множество слов любого словаря линейно упорядоче-

но в соответствии с лексикографическим порядком. Так, например, в

словаре русского языка магический магия (согласно первому из двух условий: здесь b=маги, ч я, c =еский, слово d пустое). По-

этому слово магический расположено в словаре перед словом магия.

Согласно второму условию слово маг магистр.

Пример 1.56. Пусть X {0,1} и 0 1. На множестве слов длины 3

лексикографический порядок имеет следующий вид:

000 001 010 011 100 101 110 111 .

1

Раздел 2

Алгебраические структуры

Бинарные операции

Определение 2.1. Бинарной операцией на множестве X называется любое фиксированное отображение :X X X .

Согласно этому определению, при задании бинарной опера-

ции каждой упорядоченной паре (a,b) X X ставится в соответ-

ствие однозначно определенный элемент c (a,b) множества X .

Вместо c (a,b) иногда записывают c a b, а еще чаще бинар-

ную операцию обозначают каким-нибудь специальным символом,

характеру эти операции могут существенно отличаться от известных

«обычных» операций на множестве действительных чисел. На лю-

бом множестве X могут быть заданы несколько бинарных опера-

ций. Желая выделить какую-либо из них, используют запись ( X , ),

где есть некоторая бинарная операция, и тогда говорят, что опе-