discr_math

M n (или просто в M n ).

Определение 3.22. Если некоторая формула F выполнима для лю-

бого набора ( 1, , n) M n , то она называется тождественно ис-

тинной на множестве M n .

Формула F , которая тождественно истинна на любом предметном множестве называется общезначимой.

Определение 3.23. Формула F называется тождественно ложной в

M n , если для любого упорядоченного набора ( 1, , n) M n зна-

чение F( 1, , n) 0.

Если F является тождественно ложной на любом предмет-

ном множестве M n , то формула F называется противоречивой.

Пример 3.53. Формула F1 P(x) Q(x), где P(x) и Q(x) ─ одно-

местные предикаты на R: «x2 9 0 » и « x2 4x 3 0 » соответст-

кат P соответствует неравенству « x12 x22 x23 0», а предикат Q

имеет вид « x12 x22 x23 0», является тождественно истинной на

предметном множестве R3 .

Пример 3.55. Для произвольного двуместного предиката формула

F3 x1 P(x1,x2) P(x1,x2) общезначима, поскольку выполняется на любом предметном множестве.

Пример 3.56. Формула F4 Q(x1,x2) Q(x1,x2) , где Q(x1,x2) ─

произвольный предикат, противоречива, так как не существует мно-

жества, на котором она выполнима.

Алфавит логики предикатов, очевидно, богаче алфавита ло-

гики высказываний. Поэтому для формул предикатов существуют новые равносильности, связанные с кванторами. Перечислим неко-

торые из таких равносильностей, ограничиваясь для простоты одно-

местными и двуместными предикатами.

Теорема 3.11. Справедливы следующие равносильности: 1. Законы e Моргана для кванторов:

72

2. Коммутация одноименных кванторов:

x y P(x, y) y x P(x, y) ,

x y P(x, y) y x P(x, y) .

3.Законы дистрибутивности:

x (P(x) Q(x)) x P(x) x Q(x),

x (P(x) Q(x)) x P(x) x Q(x) .

Помимо перечисленных равносильностей отметим еще тав-

тологичность следующих импликаций:

a)законы ограничения действия кванторов (сравните эти соот-

ношения с п.2 теоремы 3.11):

x (P(x) Q(x)) ← x P(x) x Q(x) ,

x (P(x) Q(x)) → x P(x) x Q(x) ;

b)для любого двуместного предиката P(x, y) импликация

y x P(x, y) x y P(x, y)

есть тавтология.

Процедуру доказательства перечисленных соотношений проиллюстрируем на примере доказательства равносильностей 1 и 2

теоремы 3.11.

Доказательство равносильности 1.

► Если P(x) — такой предикат, что формула x P(x) тождест-

венно истинна, то формула x P(x) тождественно ложна. Тогда

73

P(x) – тождественно ложный предикат, а P(x) – тождественно ис-

тинный предикат, поэтому утверждение x P(x) истинно. Мы пока-

зали, что правая и левая части формулы x P(x) x P(x) истинны одновременно, следовательно, ложны обе части тоже только одно-

временно. ◄

Доказательство равносильности 2.

► Пусть выражение x y P(x, y) тождественно истинно. Тогда предикат y P(x, y) , зависящий от переменной x, является тожде-

ственно истинным, и для любого фиксированного значения x0 вы-

ражение y P(x0, y) истинно, т.е. P(x0, y) – тождественно истин-

ный предикат переменной y . Тогда для любого фиксированного значения y0 высказывание P(x0, y0) истинно. В результате для лю-

бых произвольных, но фиксированных значений x0 и y0 высказы-

вание P(x0, y0) истинно, т.е. P(x, y) – тождественно истинный пре-

дикат. Аналогичными рассуждениями можно показать, что и истин-

ность правой части тождества y x P(x, y) равносильна тождест-

венной истинности предиката P(x, y) .◄

В заключение этого раздела рассмотрим один из известных примеров использования языка предикатов и кванторов в математи-

ческом анализе.

74

Пример 3.57. Пусть xn – числовая последовательность и lim xn a .

n

Исследуем структуру определения предела.

Сначала введем следующие предикаты:

«n N » – двуместный предикат, заданный на прямом про-

изведении N2 , где N есть множество натуральных чисел;

«| xn a| » – двуместный предикат переменных n и ,

заданный на прямом произведении N R , где символом R

обозначено множество положительных действительных чи-

сел;

n N | xn a| — формула логики предикатов (импли-

кация двух предикатов) и, по сути дела, трехместный преди-

кат, зависящий от переменных n, N и .

Навешивая на последний трехместный предикат кванторы, и связы-

вая все переменные, мы получим высказывание:

N n (n N | xn a| ) .

Утверждение «число a является пределом последовательности»

{xn}n N равносильно истинности этого высказывания:

Теперь на основе последнего тождества мы можем сформулировать

утверждение «число a не является пределом числовой последова-

тельности». В этом случае справедлива запись:

N n (n N | xn a| ) 1 ,

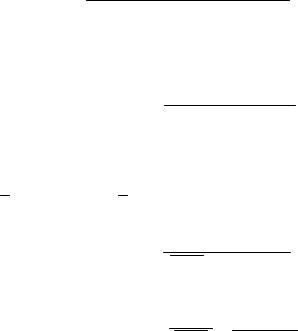
75

в которой нам необходимо избавиться от символа отрицания.

N n (n N | xn a| ) 1 .

Согласно основным законам логики предикатов, для любых двух предикатов P и Q импликация P Q равносильна дизъюнкции

P Q ((P Q) P Q). Заменяя в нашем выражении импликацию соответствующей дизъюнкцией, получим:

N n ((n N)) | xn a| 1

N n (n N | xn a| ) 1 .

Последнее утверждение можно прочитать следующим образом: «число a не является пределом числовой последовательности, если существует положительное число такое, что для любого нату-

рального числа N найдется элемент последовательности с номе-

ром бóльшим, чем N , для которого модуль разности | xn a| ».

1

Раздел 4

Графы

При необходимости проанализировать взаимосвязь между достаточно большим количеством неких однородных объектов мы,

скорее всего, непроизвольно начнем рисовать на бумаге точки (кру-

жочки), изображающие наши объекты, и соединять эти точки ли-

ниями или стрелками, отображающими интересующие нас отноше-

ния между рассматриваемыми объектами. Имея перед глазами рису-

нок (схему), легче оценить представляющие интерес взаимозависи-

мости между объектами. Такие схемы широко используют в различ-

ных областях. Это и социограммы (в психологии), и симплексы (в

топологии), и электрические цепи (в физике), и диаграммы органи-

зации (в экономике). Можно еще упомянуть сети коммуникаций,

схему метрополитена, генеалогические деревья и так далее, и так далее. Д. Кёниг первым предложил называть такие схемы «графа-

ми». Термин «граф» (от латинского слова «графио» пишу) приоб-

рел права гражданства и вошел в математический язык в 1936 году,

после выхода в свет известной монографии Кёнига, в которой впер-

2

вые графы рассматриваются как самостоятельные математические объекты независимо от их конкретного содержания.

Начало теории графов все единодушно относят к 1736 г., когда Л. Эйлер не только решил популярную в то время задачу о кёнигс-

бергских мостах1, но и нашел критерий существования в графе спе-

циального маршрута, который сегодня называют эйлеровым циклом.

Однако эти результаты Эйлера более ста лет являлись, по сути,

единственным достижением математической дисциплины, которую позднее назовут теорией графов. Лишь в середине XIX века инже-

нер-электрик Г. Кирхгоф разработал теорию графов, называемых деревьями, для исследования электрических цепей, а математик А.

Кэли в связи с описанием строения углеводородов решил перечис-

лительные задачи для трех видов деревьев. К этому же периоду от-

носится появление знаменитой проблемы четырех красок2.

Родившись при решении головоломок и занимательных игр,

теория графов в настоящее время предоставляет в распоряжение инженера исключительно удобный математический аппарат для мо-

делирования структурных свойств систем и отношений между объ-

ектами самой разнообразной природы. Благодаря наглядности и простоте этот аппарат завоевал широкое признание и повсеместно используется в инженерных исследованиях и в научно-технической

1Эйлер показал, что нельзя обойти семь городских мостов Кенигсберга и вернуться в исходную точку, пройдя по каждому мосту ровно один раз.

2Известная «нерешаемая» задача теории графов. Можно ли любую карту раскрасить только четырьмя красками так, чтобы каждые две граничащие страны не были одного и того же цвета?

3

литературе. В теоретической механике графы используются при вычислении скоростей многозвенных механизмов3.

Среди множества графов принято различать три типа: ориен-

тированные, неориентированные и смешанные графы. Некоторые авторы выделяют еще и геометрические графы.

4.1. Основные понятия и термины

Определение графа

Довольно часто в исследованиях приходится иметь дело с множествами, содержащими элементы различной математической структуры, например, элементами такого множества могут быть точки плоскости вместе с линиями, соединяющими какие-то из этих точек. Можно еще вспомнить и «школьную» алгебру (как мы уже знаем, «по-взрослому» она называется полем действительных чи-

сел), элементами которой являются и действительные числа, и опе-

рации сложения и умножения действительные чисел. Для идентифи-

кации единого целого (множества), объекты (элементы) которого имеют различное математическое строение, часто употребляют вме-

сто термина «множество» термин «совокупность», пользуясь при этом везде, где это необходимо, угловыми скобками вместо при-

вычных фигурных скобок .

3 Кирсанов М.Н. Решебник. Теоретическая механика. М.: Физматлит, 2008.

4

Предметом первых задач теории графов были конфигурации,

состоящие из точек и линий, связывающих некоторые точки. При-

меры таких конфигураций представляет рис. 4.1.

Рис 4.1

В этих задачах было совершенно безразлично, соединяют ли две концевые точки прямые линии или же эти точки соединяются криволинейными дугами. Так же не принималась во внимание и протяженность линии. Существенным и важным было только то об-

стоятельство, что каждая линия соединяет две конкретные точки.

Таким образом, обе конфигурации (графа), изображенные на рис.4.1,

идентичны. В результате рассмотрения таких задач пришли к сле-

дующему определению графа как абстрактного математического понятия.

Определение 4.1. Граф G это совокупность G V,U , где V

непустое множество, элементы которого называют вершинами гра-

фа; а U множество, элементы которого называются ребрами гра-

фа. Каждое ребро графа представляет собой неупорядоченную или