
discr_math
.pdf
15
Вес можно приписывать не только ребрам, но и вершинам.
Например, вершины, соответствующие населенным пунктам, могут характеризоваться количеством мест в гостиницах, пропускной спо-
собностью станций техобслуживания. Вообще, вес вершины означа-
ет любую характеристику соответствующего ей объекта – атомный вес элемента в структурной формуле, цвет изображаемого вершиной предмета, возраст человека и т. п.
Определение 4.4. Графы, вершинам и (или) ребрам которых припи-
саны некоторые веса, называют взвешенными графами. Графы, вер-
шины которых пронумерованы7, еще называют помеченными гра-
фами.
Особое значение для моделирования физических систем приобрели взвешенные ориентированные графы, называемые гра-
фами потоков сигналов или сигнальными графами. Вершины сиг-
нального графа отождествляются с некоторыми переменными, опи-
сывающими состояние системы, а вес каждой вершины означает функцию времени или некоторой величины, характеризующую со-
ответствующую переменную (сигнал вершины). Дуги отображают связи между переменными, и вес каждой дуги представляет собой численное или функциональное отношение, задающее передачу сиг-
нала от одной вершины к другой (передача дуги). Сигнальные графы находят широкое применение в теории цепей и систем, а также во многих других областях науки и техники.
7 Например так, как у графа G1 на рис. 4.1.
16
Степени вершин
Пусть G неориентированный граф.
Определение 4.5. Степенью вершины a графа G будем называть число (a), равное количеству звеньев графа, инцидентных верши-
не a . Вершина графа, имеющая степень 0, называется изолирован-
ной, а степень 1 висячей.
b |
|
c |
При подсчете звеньев, инцидент- |
|
|
||||
|
ных вершине a , некоторую неопределен- |
|||
|
|
|
||
a |
|
|
d |
ность вносят петли, так как их можно счи- |
|
||||
|
|
|
Рис.4.4 |
тать и как единственное, и как двойное |
|
|
|
|
звено. В зависимости от рассматриваемой |
задачи, может оказаться более удобным как тот, так и другой способ подсчета. Чтобы не возникали недоразумения, следует в каждом случае указывать, считается петля однократным звеном или двой-
ным.
Число (a,b), равное числу звеньев, соединяющих вершины
a и b, назовем кратностью этих вершин. Если у графа нет кратных
звеньев, то (a,b) 0 или (a,b) 1, при этом у неориентирован-
ных графов (a,b) (b,a) .
У графа, представленного на рис. 4.4, (b)=1 (висячая вер-
шина), (c)=0 (изолированная вершина) и |
(d) =2, если считать |
петлю однократным звеном. При этом |
(a,b) (a,d) 1, а |
(a,с) (b,c) (c,d) 0. |
|

17
Выпишем несколько простых формул. Очевидно, что сте-
пень любой вершины графа a равна сумме кратностей всех пар вершин a , b:
(a) (a,b) .
b V
Так как каждое звена графа принимается во внимание при вычислении степеней обоих его концов, то число звеньев графа m U связано со степенями и кратностью его вершин соотношени-
ем (лемма о рукопожатии) :
2m (a) (a,b).
a V a,b V
Эти формулы справедливы и при наличии у графа петель,
если только при подсчете степеней вершин петли считать дважды.
Из последней формулы следует, что сумма степеней всех вершин неографа всегда четна, следовательно,
(a) 0 (mod 2).
a V
Сумма в левой части этой формулы, естественно, останется четной даже в том случае, когда отбрасываются все четные степени вершин.
Поэтому справедлива следующая теорема.
Теорема 4.1. В конечном графе число вершин с нечетной степенью всегда четное.
Это утверждение установлено Эйлером и является историче-
ски первой теоремой теории графов.
Обратимся теперь к ориентированным графам.
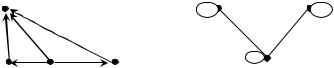
18
Определение 4.6. Полустепенью исхода (захода) вершины a графа
G будем называть число (a) (соответственно (a)), равное ко-
личеству дуг графа, исходящих из вершины a (заходящих в верши-
ну a ). Вклад каждой петли, инцидентной вершине a , равен 1 как в
(a), так и в (a).
Очевидно, что для любого ориентированного псевдографа
выполняется равенство:
(a) (a) m .
|
|
a V |
a V |
||
Вершину |
a , |
для которой (a) 0 называют стоком, а у |
|||
которой (a) 0 истоком. |
|
|
|
||
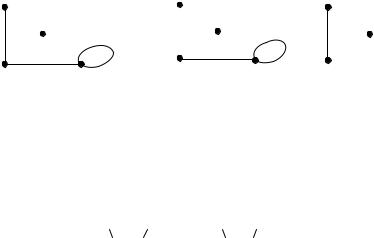
На рис. |
4.5 |
показан орграф, у которого (a) (a) 1, |
|||
(b) 0, (b) 3, (c) (c) 1, (d) 3, (d) 0. |
|||||
b |
d |
|
|
|
|
|
|
|
|
||
a |
c |
|
|
|
|
|
|
|
|
||
Рис. 4.5 |
|
|
|
Рис. 4.6 |
|
Вершина b этого графа является стоком, а вершина d истоком.

19
Типы конечных графов
Если граф не имеет ребер (т.е. U ), то все его вершины изолиро-
ваны, и он называется пустым или нуль графом.
Простой неориентированный граф, в котором любые две вершины соединены ребром, называется полным. Полный граф с n
вершинами обозначают символом Kn (рис.4.2, граф K4 ). Граф по-
рядка n без ребер называется пустым и обозначается On . Граф O1
называется тривиальным. Можно расширить полный граф до пол-
ного графа с петлями, добавляя петлю в каждой вершине (рис.4.6).
В ориентированном полном графе имеются пары ребер, по одному в каждом направлении, соединяющие любые две различные вершины.
Турниром8 называется орграф, любую пару вершин которого соединяет только одна дуга. Турнир отличается от полного ориенти-
рованного графа тем, что у него нет противоположно направленных дуг.
Граф называется однородным (регулярным) степени k , если степени всех его вершин одинаковые и равны k . Однородный граф степени 1 называется паросочетанием. Примерами однородных графов могут служить графы, образованные вершинами и ребрами пяти первых правильных многогранников (или, так их называют,
платоновых тел): тетраэдра и куба (степени 3), октаэдра (степени 4),
8 Состязание, правила которого предписывают всем его участникам встречаться друг с другом по одному разу и запрещают ничейный исход, обычно называют турниром. Поэтому турниром назвали и граф, представляющий

20
додекаэдра (степени 3), икосаэдра (степени 5). Граф третьей степени называют кубическим, он обладает рядом интересных свойств и, в
частности, всегда имеет четное число вершин. Три кубических графа изображены на рис.4.2.
Из выписанной выше формулы, связывающей число звеньев графа m со степенями его вершин, для случая однородного графа
степени k (все (a) k, a V ), получим:
n
2m k n k .
1
Напоминаем, что n V число вершин графа. Поэтому, если k
нечетное число, то n должно быть четным, и, следовательно, у лю-
бого однородного графа нечетной степени (и кубического тоже) все-
гда четное количество вершин.
Орграф называется однородным степени k , если полустепе-
ни всех его вершин одинаковые и равны k : (a)= (a)=k . В
этом случае
n
m k n k .
1
Здесь, как и раньше, n и m число вершин и дуг графа.
Если множество вершин простого графа V можно разбить на два непересекающихся подмножества (доли) V1 , V2 (V1 V2 ) и
такое состязание: вершинами графа считаются все участники состязания, и для каждой пары вершин дуга идет от победителя к побежденному.

21
при этом не существует ребер, соединяющих вершины одного и того же подмножества, то такой граф называется двудольным (иначе
биграфом). Полный двудольный (у него каждая вершина из V1 со-
единена с каждой вершиной из V2 ). обозначают символом Kn1,n2 где
n1 V1 , n2 V2 . Граф K3,3 изображен на рис 4.13.
Части графов
Еще раз напоминаем: любой граф есть совокупность множе-
ства вершин и множества ребер, при этом ребра фиксируют имею-
щиеся взаимозависимости между вершинами. Каждое ребро пред-
ставляет конкретную пару вершин, между которыми установлена такая взаимосвязь. Игнорируя взаимосвязь между какими-то двумя вершинами, мы тем самым ликвидируем (удаляем) соответствующее ребро. Операция удаления ребер порождает новый граф, с теми же вершинами, но с меньшим числом ребер. Если по каким-то сообра-
жениям отпадает необходимость принимать во внимание опреде-
ленную вершину графа, то ее следует удалить. Операция удаления вершины графа более сложная. Кроме самой вершины необходимо еще удалить и все те ребра графа, которые представляли связи уда-
ленной вершины с другими вершинами графа, т.е. все инцидентные ей ребра.
Граф H  V ,U
V ,U  , полученный в результате операций удале-
, полученный в результате операций удале-
ния вершин и (или) ребер графа G  V,U
V,U , называется частью
, называется частью
(иногда подграфом) графа G . Все вершины и ребра графа H явля-
22
ются одновременно вершинами и ребрами графа G : V V,U U .
В этом случае говорят, что H содержится в G . Нуль граф счита-
ется частью каждого графа. Граф H будет ориентированным или неориентированным в зависимости от того, каким является граф G .
Граф H1, изображенный на рис 4.8, получен в результате
b |
|
|
G |
b |
H1 |
b |
H2 |
u1 |
c |
|
|
c |
d |
|
c |
u |
2 d |
|
a |
a |
|
||
a |
u3 |
|
|||||
|
|
|
|
||||
|
Рис.4.7 |
|
Рис 4.8 |
|
|
Рис 4.9 |
|
операций удаления ребра d графа G (этот граф задан на рис. 4.7), а
граф H2 , показанный на рис. 4.9, есть результат операций удаления у того же графа G вершины d .
Пусть A некоторое подмножество множества вершин V
графа G . Часть H  A,U
A,U  графа G
графа G  V,U
V,U называется подграфом,
называется подграфом,
порожденным (или индуцированным) множеством вершин A (вер-
шинно-порожденным подграфом), если ребрами H являются толь-
ко те ребра множества U , оба конца которых принадлежат A. Он получается из графа G в результате удаления всех вершин множе-
ства V \ A и всех ребер, им инцидентных. Для единственной верши-
ны a этот подграф состоит из самой вершины a и из петель верши-
ны a , если они имеются.
23
Подграфом, порожденным множеством ребер E (реберно-
порожденным подграфом), называют часть |
|
графа G , |
H V ,E |
где E некоторое подмножество множества ребер U графа G , а
V есть множество всех вершин графа G , которые являются кон-
цами ребер множества E . Такой подграф получается из графа G
удалением всех ребер множества U \ E и последующего удаления всех изолированных вершин получившейся части.
Часть H  V,U
V,U  графа G называется его остовным под-
графа G называется его остовным под-
графом или суграфом. Так как в этом случае V V, U U , то су-
граф получается из графа G после удаления некоторых (или даже всех) его ребер.
Замечание. В некоторых работах понятия подграфа и части графа отождествляются, хотя есть исследователи, занимающиеся теорией графов, которые эти понятия различают, определяя подграф как часть, полученную в результате операции удаления у графа некоторых его вершин. Они пользуются только понятиями части, суграфа и подграфа (в указанном только что смысле). Заметим, что в этом случае любая часть H графа G есть суграф некоторого подграфа этого графа: вначале у исходного графа удаляем все вершины, не входящие в часть H (вместе с инцидентными им ребрами), а затем изымаем ребра найденного подграфа, которые не принадлежат H .
Звездный графSn , определяемый вершиной a , состоит из самой вершины a и всех n вершин графа G ей смежных, а его реб-
рами будут все ребра, инцидентные этой вершине.
Для каждой части H графа G существует единственная до-
полнительная часть графа G (дополнение) H , состоящая из всех

24
ребер G , которые не являются ребрами H , и вершин, инцидентных
этим ребрам: H G \ H .
H
H
Рис. 4.10
На рис. 4.10 видим граф H , который есть суграф полного
графа K6 , и граф H дополнение графа K6 для суграфа H .
Пусть H1 и |
H2 две части G . Сумма (объединение, нало- |
|
жение) этих частей |
H H1 H2 есть часть, состоящая из всех ре- |
|
бер (и вершин, им инцидентных), которые принадлежат или H1, или |
||
H2 , или им обоим9. Пересечением частей графа H1 и H2 назовем |
||
часть графа D H1 |
H2 , |
ребра которой являются ребрами H1 и |
H2 одновременно. |
|
|
Две части H1 и H2 |
не пересекаются по вершинам, если не |
|
имеют общих вершин, а следовательно, не имеют и общих ребер,
и две части не пересекаются по ребрам, если у них нет общих ребер.
Часть H и ее дополнение H не пересекаются по ребрам, и
G H H .
9 Граф H на рис. 4.10 , являющейся объединением двух треугольников, называется графом Давида.
