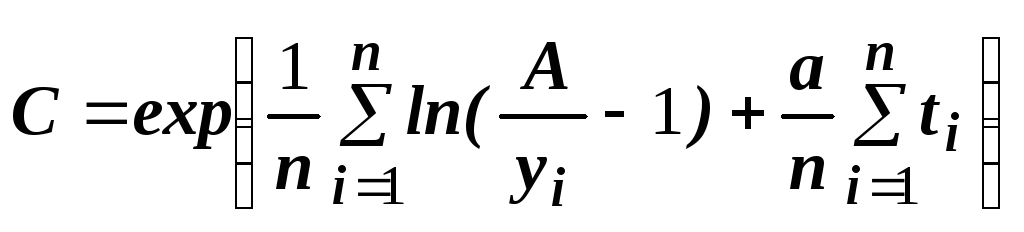Лекция 7. Множественные нелинейные регрессии

Пример нелинейной зависимости (регрессии):

(1)

–эти зависимости могут быть различными, например: первая может быть квадратичной ,вторая экспонентной и т.д.

Все эти функции считаются заранее заданными. Поэтому после выполнения замены модель является линейной.

Замена: .

(2)

Важный случай: степенная зависимость:

(3)

эта зависимость нелинейная. Здесь тоже необходима замена, но предварительно необходимо выполнить логарифмирование:

;

Линейная модель:

(4)

в результате можно получить весь вектор параметров. В этом векторе начинаем с – параметры те же, что и в исходной модели;пересчитывается вследующим образом:.

Оценка параметров логистической регрессии

Для прогнозирования спроса на отдельные товары часто используется такое уравнение:

,

(5)

где ,,– константы,,– переменные.

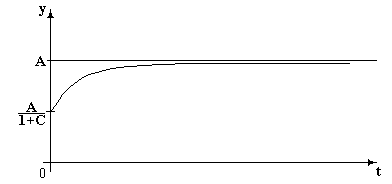
Такие уравнения получаются при анализе рынка товаров длительного пользования.

Замечено, что спрос некоторое время возрастает, а затем колеблется около константы.

Содержание: – это спрос на некоторый товар,– время,– некоторая константа, которая характеризует насыщенность рынка товаром.

Получим уравнение: скорость изменения спроса пропорциональна самому спросу и одновременно разнице между уровнем насыщенности и спросом:

(6)

Это дифференциальное уравнение первого порядка, после раскрытия скобок, превращается в следующее уравнение Бернулли:

(7)

Это уравнение можно решить аналитически.

Разностный метод решение дифференциального уравнения

Предположим, что владеем рядом динамики: величины спроса и

соответствующие моменты времени .

Дифференциальное уравнение (7) в разностной форме имеет вид:

если , тогда уравнение упростится.

Приращение – это разница двух соседних уровней ряда динамики:

.

Обозначим , тогда уравнение примет вид:

.

Количество уравнений . Это система разностных уравнений.

Если известно, анет, то можно назватьприращением теоретическим и сравнивать его с фактическим.

Фактические разности .

Необходимые условия минимума:.

Найдем частные производные:

; .

Получим систему нормальных уравнений:

.

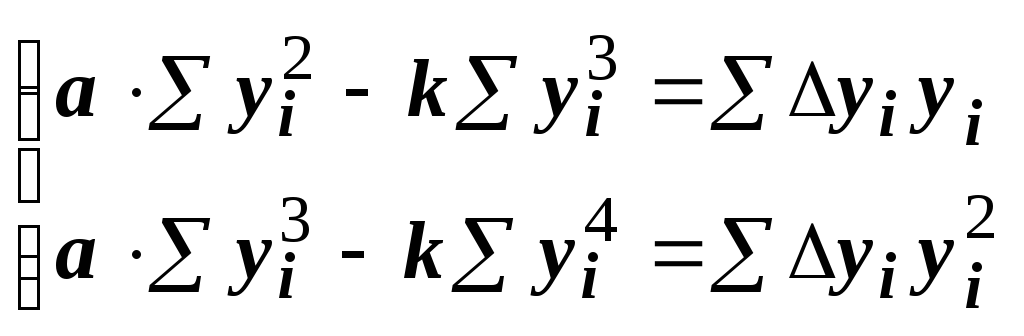Из этой системы найдем и, затем.

Решая дифференциальное уравнение (7) получим общее решение в форме (5). Константа – неизвестна.

Выполним преобразования: или.

Выполним логарифмирование полученного уравнения:

(8)

В уравнение (8) подставим все значения иво всехточках и найдем сумму уравнений:

(9)

По правилу Лопиталя :

–уровень насыщенности рынка

Экономический смысл: после некоторого времени спрос становится практически постоянным, это связано с практическим отсутствием новых потребителей товара. Потребление связано с замещением товара отслужившего соответствующий срок.

Если приращение времени , система нормальных уравнений будет сложнее.

Разностные уравнения дают несмещенные оценки параметров при малых значениях прироста .

При больших значениях иувеличиваются погрешности оценки параметров.