Головизин_Лекции / Лекция 2. Поле комплексных чисел

Если n – четное число, то существует ровно два действительных корня n-й степени из положительного числа и они являются противоположными числами, поэтому один из них положительный, его и обозначают

и называют его арифметическим, а второй будет

отрицательным, противоположным арифметическому и

его обозначают .

В любом случае, знак обозначает (при условии, что это выражение имеет смысл) только одно число, один корень.

В случае же, если – комплексное число, то для любого натурального числа n выражение всегда имеет смысл и обозначает все множество корней n-й степени из комплексного числа z.

Обозначение: , где – все n корней n-й степени из комплексного числа z, так что по определению .

В частности, при существуют ровно два корня из комплексного числа z и легко видеть, что, если – квадратный корень из комплексного числа z, то , т.е. оба корня и являются противоположными комплексными числами, поэтому вместо записи применяют запись .

Заметим, что если , то . Действительно, допустив противное, мы бы имели равенство , т.е. получили бы противоречие предположению, что .

п.6. Извлечение квадратного корня из комплексного числа. Формула квадратных корней из комплексного числа.

В дальнейшем нам понадобится одна числовая функция:

обозначим .

Эту функцию называют знаком числа х и читается она так: "сигнум икс".

Теорема. Пусть . Тогда

(7) 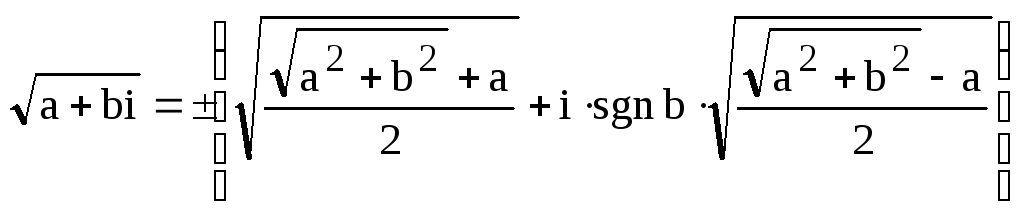, где квадратные корни в скобках являются арифметическими квадратными корнями из положительных чисел.

Доказательство. Как мы уже выяснили существует ровно два квадратных корня из комплексного числа, причем они являются противоположными числами. Пусть , где . Тогда или . Возведем в квадрат левую часть этого равенства и воспользуемся условиями равенства двух комплексных чисел. Получаем:

(8) .

Возведем в квадрат каждое уравнение этой системы: . Прибавим второе уравнение к первому:

.

Здесь – обычный арифметический квадратный корень из положительного действительного числа. Далее, если полученная система имеет решение, то по обратной теореме Виета и являются корнями квадратного уравнения . Находим дискриминант . Отсюда . Оба корня квадратного уравнения оказываются положительными, т.к., очевидно, . При выборе корней учитываем равенства (8), а именно . Отсюда следует, что и

. Осталось правильно выбрать знаки перед знаками радикалов. Из равенств (8) следует, что . Положим , тогда , откуда и следует доказываемая формула. Теорема доказана.

Пример. Вычислить .

Решение. Используем только что доказанную формулу корней. Здесь . Подставляем в формулу и получаем:

.

Ответ: .

Замечание. Можно не запоминать формулу (7) ввиду ее громоздкости, а при решении использовать алгоритм доказательства теоремы. Решим таком образом предыдущий пример.

Пусть . Тогда . Это возможно лишь тогда равны вещественные и мнимые части обоих комплексных чисел: . Возводим оба уравнения системы в квадрат: . Прибавляем второе уравнение к первому: . Применяем обратную теорему Виета:

. Решаем квадратное уравнение: . Так как , то . Принимаем . Так как , то . Получили один из двух корней: . Второй корень противоположен первому.

Ответ: .

Конечно, этот способ, в отличие от первого, занимает у нас некоторое время, но зато алгоритмы запоминаются лучше, нежели формулы.

Нам будет интересен частный случай формулы (7), когда мнимая часть числа z равна нулю.

Следствие. Пусть – произвольное действительное число. Тогда имеет место следующая формула:

(9) .

Доказательство очевидно, достаточно подставить в формулу (7) и вспомнить, что арифметический квадратный корень из квадрата действительного числа равен его модулю: .

Теперь, если , то формула (9) дает оба корня из положительного действительного числа а: .

Не будем забывать, что квадратный корень в левой части формулы (9) обозначает все множество корней из комплексного числа , а квадратные корни в правой части формулы (9) обозначают арифметические квадратные корни из неотрицательных действительных чисел. Обозначение одно и то же, с помощью знака радикала, а смысл различный.

Пусть теперь . Тогда и формула (9) дает равенство: . Здесь – арифметический квадратный корень из положительного числа .

Случай очевиден: .

Интерес представляет случай корня квадратного из отрицательного числа. Сформулируем этот случай отдельно в виде следствия.

Следствие. Пусть и . Тогда оба квадратных корня из числа z могут быть найдены по формуле:

(10) .

Примеры: , , .

Замечание. Обратите внимание на последнее равенство:

.

Это верное равенство, т.е. по определению есть множество всех корней из числа –1, в то время как равенство неверное, с этой точки зрения! Именно поэтому нельзя переносить свойства корней из действительных чисел на корни из комплексных чисел, как показывает следующий простой пример.

Пример. Найдите ошибку в следующих преобразованиях:

.

С другой стороны, легко доказать следующую теорему.

Теорема. (О вынесении действительного множителя из под знака корня.) Пусть, n – произвольное натуральное число. Тогда

(11) ,

где есть обычный арифметический корень из положительного числа.

Доказательство. Равенство (11) здесь нужно понимать как равенство двух множеств: – множество всех корней n-й степени из комплексного числа , – множество всех корней n-й степени из комплексного числа z,

.

Отсюда вытекает и способ доказательства. Мы докажем, что оба множества состоят из одних и тех же элементов.

Пусть . Тогда . Отсюда следует, что . Обратно, Пусть . Тогда . Следовательно, , ч.т.д. Теорема доказана.

Замечание. Предыдущее следствие можно вывести и из только что доказанной теоремы.

Следствие. Пусть и Тогда .

Доказательство. Рассматриваем отрицательное число а как комплексное число . Тогда доказываемое равенство сразу же следует из только что доказанной теоремы: .

Пример. Вычислить .

Решение. Применим только что доказанную теорему: .

Ответ: .

п.7. Решение квадратных уравнений в поле комплексных чисел.

Вывод формулы корней квадратного уравнения в поле комплексных чисел ничем не отличается от такового в поле действительных чисел (как, впрочем, и в любом поле, в том числе и в конечном). Вспомним этот вывод.

Теорема. Пусть , z – комплексная переменная. Тогда квадратное уравнение имеет ровно два корня (они могут быть равными), которые можно найти по формуле: .

Доказательство. Выделим полный квадрат в левой части квадратного уравнения:

.

Теперь квадратное уравнение можно записать в виде:

. Здесь мы применили следствие из п.6. Доказываемая формула очевидно следует из последнего равенства.

Теорема доказана.

Пример. Решить уравнение .

Решение. Вычисляем дискриминант

. Вычисляем корни из дискриминанта по формуле квадратных корней из комплексного числа:

.

Вычисляем корни уравнения по формуле корней квадратного уравнения:

или ; .

Ответ: .

Замечание. Аналогично решаются квадратные уравнения с действительными коэффициентами, но с отрицательным дискриминантом.

Пример. Решить уравнение .

Решение. Вычислим дискриминант. . Отсюда следует, что действительных корней квадратное уравнение не имеет, но, согласно теореме, оно имеет два корня в поле комплексных чисел. Для вычисления корня из дискриминанта применяем следствие из предыдущего п.6, смотри там же пример. Получаем:

. Теперь подставляем в формулу корней квадратного уравнения: .

Ответ: .