
Головизин_Лекции / Лекция 3. Линейные операции с векторами
.docЛекции по алгебре и геометрии. Семестр 1.
Лекция 3. Векторная алгебра. Линейные операции над векторами.
Краткое содержание: функция расстояния и ее свойства, определение вектора как направленного отрезка, модуль вектора, коллинеарные векторы, порядок следования точек прямой, положительное направление, ось, ориентация вектора на оси, сонаправленные и противоположно направленные векторы, равенство векторов, линейные операции с векторами, векторные пространства векторов прямой, плоскости и пространства, необходимые и достаточные условия коллинеарности двух векторов.
Глава 3. Линейные операции над векторами.
п.1. Функция расстояния.
Буквой L будем обозначать прямую, буквой Р – плоскость, S – пространство. Полагаем, что прямая, плоскость и пространство состоит из точек, т.е. L, P и S являются множествами, элементами которых являются точки.
Что есть точка, прямая, плоскость или пространство, никто не знает. В геометрии эти понятия вместе с их свойствами вводятся с помощью аксиом. Мы можем только строить на чертеже модели этих понятий, чтобы получить о них какое-то геометрическое представление. В дальнейшем мы полагаем, что выполняются все аксиомы элементарной геометрии, которая изучается в средней школе.
Мы
также будем полагать, что нам известно
расстояние между любыми двумя точками
пространства. Обозначение. Расстояние
между двумя точками А и В мы будем
обозначать
![]() или
или
![]() .
.
Кроме того, мы считаем известным свойства расстояния как функции двух аргументов:
1. Свойство неотрицательности:
![]()
![]() и
и
![]() .
.
2. Свойство симметричности:
![]()
![]() .
.
3. Неравенство треугольника:
![]()
![]() ,
,
причем равенство выполняется лишь в том случае, когда
точка у лежит на отрезке прямой хz или zx.
х у z

 |
|
|
|
|
|
или z у х
п.2. Определение вектора, как направленного отрезка.
Определение.
Вектором, как направленным отрезком,
называется упорядоченная пара точек
(А, В) и обозначается
![]() .
Точка А называется началом вектора
.
Точка А называется началом вектора
![]() ,
точка В называется концом вектора
,
точка В называется концом вектора
![]() .
.
Геометрическое изображение вектора.
Вектор изображается отрезком прямой, соединяющим точки А и В и стрелкой в точке В:
А В
В
Определение.
Длиной или модулем вектора
![]() называется длина отрезка АВ, т.е.
расстояние между точками А и В.
называется длина отрезка АВ, т.е.
расстояние между точками А и В.
Модуль вектора
![]() обычно обозначается
обычно обозначается
![]() .
Таким образом, по определению
.
Таким образом, по определению
![]() .
.
Множество всех
векторов, как направленных отрезков в
пространстве точек S,
будем обозначать буквой
![]() .
.
Замечание. Через
любые две точки можно провести единственную
прямую. Проведем прямую L
через начало А и конец В вектора
![]() .
Тогда все точки отрезка АВ будут являться
точками прямой L. Мы будем
говорить, что вектор
.
Тогда все точки отрезка АВ будут являться
точками прямой L. Мы будем
говорить, что вектор
![]() лежит на прямой L.
лежит на прямой L.
Обозначение.
Обозначим через
![]() множество всех векторов, лежащих на
прямой L или на любой
другой прямой, параллельной прямой L.
множество всех векторов, лежащих на
прямой L или на любой
другой прямой, параллельной прямой L.
Коллинеарные векторы.
Определение. Два вектора называются коллинеарными, если они лежат на одной или на параллельных прямых.
Обозначение.
Если векторы
![]() и
и
![]() коллинеарные, то это обозначается так:
коллинеарные, то это обозначается так:
![]() .
.
п.3. Отношение порядка следования на множестве.
Пусть М произвольное
конечное множество, т.е. состоящее из
конечного числа элементов. Допустим,
что мы хотим выписать все его элементы.
Какой элемент выписать первым? Какой –
вторым? И так далее. Ясно, что если число
элементов данного множества больше
одного, то это можно сделать различными
способами. Например,
![]() .
Тогда все три элемента этого множества
можно выписать шестью различными
способами: 1, 2, 3 или 1, 3, 2 или 2, 1, 3 или 2,
3, 1 или 3, 1, 2 или 3, 2, 1. Если мы выбираем
один какой-то способ, то тем самым мы
упорядочиваем множество, т.е. вводим на
множестве отношение порядка следования.
.
Тогда все три элемента этого множества
можно выписать шестью различными
способами: 1, 2, 3 или 1, 3, 2 или 2, 1, 3 или 2,
3, 1 или 3, 1, 2 или 3, 2, 1. Если мы выбираем
один какой-то способ, то тем самым мы
упорядочиваем множество, т.е. вводим на
множестве отношение порядка следования.
Пусть множество
М состоит из n элементов.
Выпишем все его элементы в каком-нибудь
порядке. Для этого пронумеруем все
элементы натуральными числами от 1 до
n. Обозначим через
![]() первый элемент, через
первый элемент, через
![]() второй элемент и т.д. Получаем:
второй элемент и т.д. Получаем:
![]() .
Теперь мы можем сказать, что элемент
.
Теперь мы можем сказать, что элемент
![]() предшествует элементу
предшествует элементу
![]() ,
или элемент
,
или элемент
![]() следует за элементом
следует за элементом
![]() .
И, вообще, для любых элементов
.
И, вообще, для любых элементов
![]() мы можем сказать, что если
мы можем сказать, что если
![]() ,
то
,
то
![]() предшествует элементу
предшествует элементу
![]() или элемент
или элемент
![]() следует за элементом
следует за элементом
![]() .
.
Определение. Пусть М произвольное множество, не обязательно конечное. Говорят, что на множестве М определено отношение строгого линейного порядка следования элементов, если выполняются следующие свойства.
1. Для любых двух различных его элементов указано какой из этих элементов следует за другим (предшествует другому).
2. Свойство
транзитивности. Пусть
![]() .
Если элемент а предшествует элементу
b (b следует
за а), а элемент b предшествует
элементу с (с следует за b),
то элемент а предшествует элементу с
(с следует за а).
.
Если элемент а предшествует элементу
b (b следует
за а), а элемент b предшествует
элементу с (с следует за b),
то элемент а предшествует элементу с
(с следует за а).
3. Никакие два различных элемента не могут одновременно предшествовать друг другу (следовать друг за другом).
п.4. Порядок следования точек прямой. Определение оси.
На любой прямой можно естественным образом установить (причем только двумя способами) строгий линейный порядок следования ее точек. Грубо говоря, слева направо или наоборот, см. ниже рисунки 1 и 2.
L

 |
|
|
|
А В
рис.1.
L
 |
|
|
|
В А
рис.2.
В обоих случаях точка А предшествует точке В, соответственно точка В следует за точкой А. Геометрически порядок следования точек на прямой L изображается с помощью стрелки.
Определение. Если на прямой выбран один (из двух возможных) порядок следования точек, то говорят, что на прямой выбрано положительное направление.
Определение. Прямая, на которой выбрано положительное направление называется осью.
Определение.
Мы будем говорить, что вектор
![]() коллинеарен оси L и писать
коллинеарен оси L и писать
![]() ,
если вектор
,
если вектор
![]() лежит на оси L или лежит
на прямой, параллельной оси L.
лежит на оси L или лежит
на прямой, параллельной оси L.
п.5. Ориентация вектора, лежащего на оси. Сонаправленные и противоположно направленные векторы.
Пусть L
произвольная ось и вектор
![]() ,
лежит на оси L. Может быть
два случая, см. рисунки 3 и 4:
,
лежит на оси L. Может быть
два случая, см. рисунки 3 и 4:
А В L

 |
|
|
|
рис. 3.
L

 |
|
|
|
В А
рис. 4.
В одном случае (рис.3) начало вектора – точка А предшествует концу вектора, точке В, а во втором случае наоборот, начало вектора следует за его концом.
Определение. Вектор, лежащий на оси, называется сонаправленным с осью, если его начало предшествует его концу (конец вектора следует за его началом).
В противном случае (как на рис.4) говорят, что вектор и ось имеют противоположные направления.
Если
вектор
![]() сонаправлен с осью L, то
этот факт мы будем обозначать так:
сонаправлен с осью L, то
этот факт мы будем обозначать так:
![]() .
Если вектор
.
Если вектор
![]() и ось L имеют противоположные
направления, то
и ось L имеют противоположные
направления, то
![]() .
.
Определение.
Вектор
![]() ,
лежащий на оси L, называется
правоориентированным, если
,
лежащий на оси L, называется
правоориентированным, если
![]() и называется левоориентированным, если
и называется левоориентированным, если
![]() .
.
На
рис.3 вектор
![]() правоориентирован на оси L,
а на рис.4 – левоориентирован.
правоориентирован на оси L,
а на рис.4 – левоориентирован.
Определение. Два вектора, лежащие на одной прямой называются сонаправленными, если при любом выборе положительного направления на этой прямой оба вектора будут иметь одинаковую ориентацию. В противном случае векторы называются противоположно направленными.
Обозначение.
![]() – векторы
– векторы
![]() и
и
![]() сонаправленные,
сонаправленные,
![]() – векторы
– векторы
![]() и
и
![]() имеют противоположные направления
(противоположно направлены).
имеют противоположные направления
(противоположно направлены).
Пусть теперь два
вектора
![]() и
и
![]() лежат на параллельных прямых. Тогда обе
прямые лежат в одной плоскости. Проведем
секущую АС (Через начала
векторов). При этом возможны два случая.
См. рисунки 5 и 6:
лежат на параллельных прямых. Тогда обе
прямые лежат в одной плоскости. Проведем
секущую АС (Через начала
векторов). При этом возможны два случая.
См. рисунки 5 и 6:
 А
В а
А
В а

 С
D
b
С
D
b


рис. 5.
 А
В а
А
В а




D C b
рис. 6.
Секущая АС, проведенная через начала обоих векторов делит плоскость, в которой лежат обе параллельные прямые а и b, на две полуплоскости. В первом случае (рис.5) концы векторов лежат в одной полуплоскости, а во втором случае (рис.6) – в разных полуплоскостях.
Определение. Два вектора, лежащие на параллельных прямых, называются сонаправленными, если их концы лежат в одной полуплоскости относительно прямой, проведенной через их начала. В противном случае говорят, что векторы имеют противоположные направления (противоположно направлены).
Обозначения сонаправленных векторов здесь такое же, как и в случае, когда оба вектора лежат на одной прямой:
![]() – векторы
– векторы
![]() и
и
![]() сонаправленные,
сонаправленные,
![]() – векторы
– векторы
![]() и
и
![]() имеют противоположные направления
(противоположно направлены).
имеют противоположные направления
(противоположно направлены).
Определение. Пусть а и b две параллельные оси. На каждой оси возьмем по одному правоориентированному вектору. Если эти векторы сонаправленные, то данные оси называются сонаправленными. В противном случае говорят, что оси имеют противоположные направления.
Обозначения для сонаправленных и противоположно направленных осей такое же, как и для векторов.
п.6. Равенство векторов.
Определение. Два вектора называются равными, если они сонаправленные и имеют равные модули.
Иначе,
![]() .
.
Равные
векторы можно обозначать одной буквой
(с чертой или со стрелкой):
![]() .
В этом случае говорят, что вектор
.
В этом случае говорят, что вектор
![]() отложен от точки А. Если
отложен от точки А. Если
![]() ,
то говорят, что вектор
,
то говорят, что вектор
![]() отложен от точки С. Таким образом, любой
вектор можно отложить от любой точки
пространства S.
отложен от точки С. Таким образом, любой
вектор можно отложить от любой точки
пространства S.
Замечание.
На самом деле, понятие равенства векторов
расширяет само понятие вектора. Если
первоначально под вектором мы понимали
упорядоченную пару точек пространства
S, т.е. направленный отрезок,
то теперь под вектором мы будем понимать
множество в с е х направленных отрезков,
сонаправленных друг с другом и имеющих
одинаковую длину. Если один и тот же
вектор отложить от двух различных точек,
например,
![]() ,
то направленный отрезок
,
то направленный отрезок
![]() можно совместить с направленным отрезком
можно совместить с направленным отрезком
![]() с помощью параллельного переноса. Часто
направленные отрезки
с помощью параллельного переноса. Часто
направленные отрезки
![]() и
и
![]() называются представителями одного и
того же вектора
называются представителями одного и
того же вектора
![]() .
.
п.7. Сложение векторов.
Пусть
![]() – множество всех векторов пространства
точек S. Определим на этом
множестве операцию сложения векторов.
– множество всех векторов пространства
точек S. Определим на этом
множестве операцию сложения векторов.
Определение.
Пусть
![]() – два произвольных вектора.
– два произвольных вектора.
Отложим
вектор
![]() ,
от какой-нибудь точки А и обозначим его
конец буквой В, так что
,
от какой-нибудь точки А и обозначим его
конец буквой В, так что
![]() .
Вектор
.
Вектор
![]() отложим от точки В (от конца первого
вектора) и обозначим его конец буквой
С, так что
отложим от точки В (от конца первого
вектора) и обозначим его конец буквой
С, так что
![]() Тогда вектор
Тогда вектор
![]() называется суммой векторов
называется суммой векторов
![]() и
и
![]() и обозначается
и обозначается
![]() .
.
А
![]() В
В
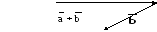

С
рис. 7.
Это правило сложения векторов носит название правило треугольника.
Существует еще одно правило сложения векторов, которое называется правилом параллелограмма и дает точно такой же результат.
Оба
вектора
![]() и
и
![]() отложим от одной точки А и обозначим
через В конец вектора
отложим от одной точки А и обозначим
через В конец вектора
![]() ,
через D – конец вектора
,
через D – конец вектора
![]() .
.
Достраиваем до
параллелограмма. Через точку D
проводим прямую параллельную АВ, через
точку В – прямую параллельную AD,
точку пересечения построенных прямых
обозначим буквой С. Тогда ABCD
– параллелограмм. Вектор
![]() .
См. рис.8:
.
См. рис.8:
А
![]() В
В
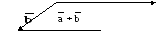


D С
рис. 8.
Равенство
![]() следует из равенства векторов
следует из равенства векторов
![]() и из определения, т.е. из правила
треугольника сложения векторов.
и из определения, т.е. из правила
треугольника сложения векторов.
Определение. Вектор, начало и конец которого совпадают, называется нулевым вектором.
Обозначение
нулевого вектора:
![]() .
.
Заметим, что модуль нулевого вектора равен нулю:
![]() .
Более того, нулевой вектор является
нулевым элементом относительно сложения
векторов. Этот факт сразу же следует из
правила треугольника сложения векторов.
.
Более того, нулевой вектор является
нулевым элементом относительно сложения
векторов. Этот факт сразу же следует из
правила треугольника сложения векторов.
Полагаем также, по определению, что нулевой вектор коллинеарный любому вектору и, более того, сонаправленный с любым вектором и, одновременно, противоположно направлен любому вектору.
Определение.
Вектор
![]() называется противоположным вектору
называется противоположным вектору
![]() ,
если:
,
если:
1)
![]() ,
т.е. они имеют противоположные направления;
,
т.е. они имеют противоположные направления;
2)
![]() – имеют равные модули.
– имеют равные модули.
Обозначение.
Вектор противоположный вектору
![]() обозначается
обозначается
![]() .
.
Из
определения противоположного вектора
следует, что если
![]() ,
то
,
то
![]() .
Действительно,
.
Действительно,
![]() и
и
![]() .
Из правила сложения векторов (правило
треугольника) сразу же следует, что
сумма противоположных векторов равна
нулевому вектору:
.
Из правила сложения векторов (правило
треугольника) сразу же следует, что
сумма противоположных векторов равна
нулевому вектору:
![]() ,
т.е.
,
т.е.
![]() .
.
п.8. Свойства сложения векторов.
1.
Сложение векторов подчиняется закону
ассоциативности, т.е.
![]() верно равенство:
верно равенство:
![]() (1)
(1)
Доказательство.
Воспользуемся правилом треугольника
сложения векторов. Пусть
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
Отложим вектор
.
Отложим вектор
![]() от точки С и обозначим его конец буквой
D, так что
от точки С и обозначим его конец буквой
D, так что
![]() .
.
Тогда по правилу
треугольника
![]() .
С другой стороны, отложим вектор
.
С другой стороны, отложим вектор
![]() и
и
![]() ,
ч.т.д. См. также рис. 9.
,
ч.т.д. См. также рис. 9.
А
![]() В
В
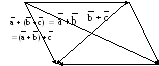
![]()
D
![]() С
С
рис. 9.
2. Существует нулевой элемент относительно сложения векторов, т.е. нулевой вектор:
![]() верны равенства
верны равенства
![]() .
.
3. Для любого вектора
![]() существует противоположный ему вектор
существует противоположный ему вектор
![]() ,
такой, что
,
такой, что
![]() .
.
4. Сложение векторов
подчиняется закону коммутативности,
т.е.
![]() верно равенство:
верно равенство:
![]() .
.
Последнее свойство сразу же следует из правила параллелограмма сложения векторов.
Таким образом, мы
видим, что множество всех векторов
![]() относительно операции сложения является
абелевой группой, очевидно, бесконечной.
относительно операции сложения является
абелевой группой, очевидно, бесконечной.
п.9. Умножение вектора на число.
Определение.
Произведением вектора
![]() на действительное число
на действительное число
![]() называется вектор
называется вектор
![]() ,
удовлетворяющий следующим двум условиям:
,
удовлетворяющий следующим двум условиям:
1)
![]() ;
;
2)
![]() ,
если
,
если
![]() и
и
![]() ,
если
,
если
![]() ;
;
и
обозначается
![]() .
.
Теорема. (Свойства умножения вектора на число.)
1.
Свойство ассоциативности:
![]() верно
верно
равенство
![]() .
.
2. Свойство дистрибутивности умножения относительно
сложения чисел:
![]() верно равенство
верно равенство
![]() .
.
3. Свойство дистрибутивности умножения относительно
сложения векторов:
![]() верно равенство
верно равенство
![]() .
.
4.
![]() верно равенство
верно равенство
![]() .
.
Доказательство. Свойство 4 вытекает из определения умножения вектора на число. Докажем свойство 1.
Умножение вектора
![]() на число
на число
![]() можно интерпретировать как гомотетию
можно интерпретировать как гомотетию
![]() какой-нибудь
плоскости Р, в которой лежит данный
вектор, с центром гомотетии в начале
вектора и коэффициентом
какой-нибудь
плоскости Р, в которой лежит данный
вектор, с центром гомотетии в начале
вектора и коэффициентом
![]() .
.
Такая гомотетия
плоскости Р оставляет точку А на месте,
![]() ,
а конец вектора – точку В переводит
(отображает) в точку С,
,
а конец вектора – точку В переводит
(отображает) в точку С,
![]() ,
причем
,
причем
![]()
и
точка С лежит на луче АВ, если
![]() и на
и на
противоположном
луче, если
![]() .
См. рис. 10 и 11.
.
См. рис. 10 и 11.
А В С




рис. 10.
С А В

рис.11.
Теперь
свойство 1 следует из того что композиция
гомотетий (т.е. последовательное их
выполнение) есть гомотетия, причем
![]() и
и
![]() верно равенство:
верно равенство:
![]() .
.
Пусть
![]() .
.
D А В С




 |
|
