Головизин_Лекции / Лекция 6. Основные задачи АГ

Лекции по алгебре и геометрии. Семестр 1.

Лекция 6. Основные задачи аналитической геометрии на плоскости и в пространстве.

Краткое содержание: расстояние между двумя точками на плоскости и в пространстве, модуль вектора, направляющие углы и косинусы вектора, орт вектора, деление отрезка в данном отношении, ГЦТ системы из двух и более материальных точек, ГЦТ треугольника, точка пересечения биссектрис треугольника.

Глава 6. Основные задачи аналитической геометрии на плоскости и в пространстве.

п.1. Расстояние между точками на плоскости и в пространстве.

Мы выведем формулу расстояния между любыми двумя точками в пространстве. Случай на плоскости будет следовать из общей формулы как частный случай.

Рассмотрим предварительно частный случай. Пусть вектор коллинеарный какой-нибудь координатной оси, например, Ох.

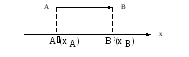
рис.1.

Расстояние между точками А и В равно:

. (1)

Ординаты и аппликаты точек А и В в этом случае равны:

, .

Формула, аналогичная формуле (1) имеет место и в случаях, когда или .

Рассмотрим теперь общий случай расположения точек А и В в пространстве относительно системы координат Охуz.

Пусть и – две произвольные точки пространства. Проведем через точки А и В плоскости параллельные координатным плоскостям. Эти 6 плоскостей высекают прямоугольный параллелепипед. См. рис.2.

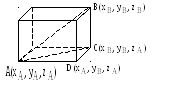
рис.2.

Из прямоугольного треугольника ADC по теореме Пифагора , а из прямоугольного треугольника АВС:

.

Так как точки А, D, С лежат в плоскости перпендикулярной оси Оz, то , т.к. , то .

Точки В, С, D лежат в плоскости перпендикулярной оси Оу, поэтому и , откуда следует, что .

Теперь, по формулам, аналогичным формуле (1), имеем:

,

,

,

откуда следует равенство:

.

Таким образом мы доказали следующую теорему.

Теорема. Пусть и . Тогда

. (2)

Следствие. Пусть и . Тогда

.

п.2. Модуль вектора, его направляющие углы и косинусы. Координаты орта вектора.

Теорема. (О модуле вектора.)

Модуль вектора равен корню квадратному из суммы квадратов его координат.

Иначе, если , то

. (3)

Доказательство. Пусть . Тогда равны их модули и их декартовые координаты: и

, , .

Подставляя в формулу (2), получаем (3), ч.т.д.

Теорема доказана.

Обозначим углы между вектором и координатными осями: , , .

Определение. Углы между вектором и координатными осями называются направляющими углами вектора.

рис.3.

Пусть . По теореме о вычислении проекции вектора на ось, имеем: , , . Отсюда следует:

, , , (4)

. (5)

Из последнего равенства следует, что орт вектора , т.е. вектор единичной длины и сонаправленный с имеет декартовые координаты:

. (6)

А т.к. , то по теореме о модуле вектора, получаем:

, откуда следует

. (7)

п.3. Деление отрезка в данном отношении.

Теорема. (О делении точки в данном отношении.)

Пусть точка С делит отрезок АВ в отношении , считая от точки А и О – произвольная точка. Тогда

. (8)

Доказательство. По определению . По правилу треугольника сложения векторов имеем: , . Подставляя в равенство , получаем: , откуда и следует (8).

Теорема доказана.

Следствие 1. (О координатах точки, делящей отрезок.) Пусть , и – три произвольные точки пространства, лежащие на одной прямой и точка С делит отрезок АВ в отношении , считая от точки А. Тогда:

1), , . (9)

2) , (10)

Доказательство. Пусть в равенстве (8), точка О(0; 0; 0) является началом координат. Тогда векторы и являются радиус-векторами точек А, В и С соответственно и , и .

Теперь, в соответствии с теоремой о действиях с векторами в координатной форме, равенства (9) сразу же получаются из равенства (8), а каждое из равенств (10) следуют из равенств (9) после очевидных алгебраических преобразований.

Следствие доказано.

Следствие 2. Если точка С есть середина отрезка АВ, где , и , то , , . (11)

Доказательство очевидно, т.к. в этом случае .

Аналогичные формулы имеют место и для случая координатной плоскости.

п.4. Геометрический центр тяжести системы из двух материальных точек.

Рассмотрим модель рычажных весов, находящихся в равновесии.

рис.4.

Здесь обозначено: АВ – отрезок, заменяющий в нашей модели однородный стержень, массу которого мы полагаем пренебрежимо малой по сравнению с массой грузов и , закрепленных на его концах. С – точка опоры всей системы. Из механики нам известно, что такая система находится в равновесии, если выполняется равенство:

,

где АС и ВС – длины соответствующих отрезков.

(Это равенство следует из равенства двух крутящих моментов, создаваемых силами тяжести данных грузов относительно точки опоры.)

Определение. Упорядоченная пара , где А – точка, – положительное действительное число называется материальной точкой, число при этом называется массой этой точки.

Определение. Пусть имеется отрезок АВ, концы которого являются материальными точками с массами и соответственно. Точка С отрезка АВ, для которой выполняется равенство

, (12)

где АС и ВС – длины соответствующих отрезков, называется геометрическим центром тяжести (в дальнейшем просто ГЦТ) системы из двух материальных точек.

Из определения следует, что ГЦТ системы из двух материальных точек А и В является точка С, которая делит отрезок АВ внутренним образом в отношении

. (13)

Теорема. (О ГЦТ системы из двух материальных точек.)

Пусть А и В две произвольные материальные точки с массами и соответственно и точка С – их ГЦТ. Тогда для любой точки О справедливо равенство:

. (14)

Для доказательства достаточно подставить в формулу (8), откуда и следует равенство (14).

Теперь, если в пространстве точек S ввести ПДСК Охуz, то, зная координаты материальных точек А, В и их массы, можно найти координаты их ГЦТ.

Следствие. (О координатах ГЦТ системы двух материальных точек.) Пусть , – две произвольные материальные точки с массами и соответственно. Пусть точка является их ГЦТ. Тогда

, , (15)

. (16)

Доказательство. Выберем в формуле (14) в качестве точки О начало координат. Тогда формулы (15) и (16) следуют из формулы (14) в соответствии с теоремой о действиях с векторами в координатной форме.

Следствие доказано.

п.5. ГЦТ системы из трех и более материальных точек.

Пусть А, В, С – система из трех материальных точек с массами , и соответственно. Заменим в этой системе две материальные точки, например, А и В материальной точкой D с массой , которая является их ГЦТ. Координаты точки D можно найти по формулам (15) и (16). Теперь у нас осталась система из двух материальных точек D и С с массами и соответственно. Обозначим через F их ГЦТ. Координату точки F опять можно найти по формулам (15) и (16), зная координаты точек D и С. Точка F называется ГЦТ системы из трех материальных точек А, В и С.

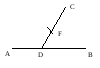
рис.5.

Вообще ГЦТ системы из n () материальных точек определяется индукцией по их количеству.

Определение. ГЦТ системы из n () материальных точек с массами называется ГЦТ системы из двух материальных точек: С и с массами и соответственно, где С – ГЦТ системы из -й материальных точек .

Теорема. (О ГЦТ системы из n материальных точек.)

Пусть – система из n () материальных точек с массами соответственно и С является их ГЦТ. Тогда для любой точки О верно равенство:

. (17)

Доказательство проводится методом математической индукции и предоставляется читателю.

Также, как и в случае двух материальных точек из формулы (17) получаются следующие формулы.

Следствие. (О ГЦТ системы из n материальных точек.)

Пусть – система из n () материальных точек с массами соответственно и С является их ГЦТ. Тогда

, (18)

, (19)

. (20)

п.6. ГЦТ треугольника.

Пусть АВС треугольник, который мы будем рассматривать как треугольную пластинку, выполненную из однородного материала, толщиной которой мы пренебрежем. Известно, что центром тяжести такой пластинки является точка пересечения медиан.

Рассмотрим теперь систему из трех материальных точек А, В и С с равными массами, сумма которых равна массе треугольника, т.е.

, (21)

где М – масса треугольника АВС.

Из определения ГЦТ системы из двух материальных точек следует, что в данном случае ГЦТ материальных точек А и В равной массы лежит на середине отрезка АВ, которую мы обозначим буквой D. Действительно, по формуле (13) имеем: и , т.е. D – середина АВ. Полагаем далее, что .

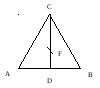
рис.6

Пусть F – ГЦТ системы из двух материальных точек D и С. Тогда по формуле (13): , откуда следует, что , т.е. F является точкой пересечения медиан.

С другой стороны, применяя формулы (18) – (20), получаем:

, , (22)

. (23)

Определение. Точка пересечения медиан треугольника называется ГЦТ этого треугольника.

Заметим, что точное определение ГЦТ геометрических фигур будет дано в курсе математического анализа при изучении кратных интегралов.

Таким образом мы доказали теорему.

Теорема. ГЦТ из трех материальных точек с равными массами совпадает с ГЦТ треугольника с вершинами в данных точках.

Как следствие, мы получили формулы (22), (23) для вычисления координат точки пересечения медиан треугольника, по известным координатам его вершин.

п.7. Центр вписанной в треугольник окружности.

Теорема. Пусть АВС произвольный треугольник, а, b, с длины сторон, лежащие против вершин А, В и С соответственно, М – точка пересечения его биссектрис. Тогда для любой точки О верно равенство

. (24)

Доказательство.

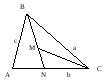
рис.7.

Пусть BN – биссектриса и М – точка пересечения биссектрис. Тогда по основному свойству биссектрисы треугольника . По свойству пропорций

, откуда и .

СМ – биссектриса треугольника BNС, поэтому

.

Докажем, что точка М является ГЦТ системы из трех материальных точек А, В и С с массами а, b и с соответственно.

Действительно, , откуда по формуле (13) следует, что точка N есть ГЦТ точек А и С. Положим . Тогда и, опять же по формуле (13) получаем, что точка М есть ГЦТ материальных точек N и В, т.е. точка М является по определению ГЦТ системы материальных точек А, В и С. Теперь, доказываемая формула (24) следует из формулы (17).

Теорема доказана.

Следствие. Пусть АВС произвольный треугольник, а, b, с длины сторон, лежащие против вершин А, В и С соответственно, М – точка пересечения его биссектрис, О – начало координат. Тогда:

, , .

Доказательство следует из (24) и теоремы о действиях с векторами в координатной форме.