Головизин_Лекции / Лекция 5. ПДСК плоскости и пространства

Лекции по алгебре и геометрии. Семестр 1.

Лекция 5. Прямоугольные декартовые системы координат на плоскости и в пространстве.

Краткое содержание: ориентация двух координатных осей на плоскости, координатный угол, координаты точки плоскости, декартовые системы координат на плоскости – общая и прямоугольная, ориентация трех взаимно перпендикулярных координатных осей в пространстве, координата точки пространства, декартовая прямоугольная система координат в пространстве, декартовые координаты вектора, координатная форма записи вектора, действия с векторами в координатной форме записи, вычисление декартовых координат вектора.

Глава 5. Прямоугольные декартовые системы координат на плоскости и в пространстве.

п.1. Ориентация двух координатных осей на плоскости.

Пусть Ох и Оу – две неколлинеарные координатные оси, точка О пересечения которых является их общим началом координат. В зависимости от выбора направлений на координатных осях возможны 4 случая.

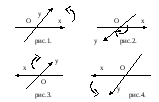
Рассмотрим кратчайший поворот оси Ох к оси Оу вокруг точки О до положения сонаправленности осей: . На рисунках 1 и 4 такой поворот осуществляется против часовой стрелки, а на рисунках 2 и 3 – по часовой стрелки. С этой точки зрения существует две принципиально различные возможности ориентации координатных осей на плоскости.

Определение. Говорят, что упорядоченная пара двух неколлинеарных координатных осей имеет правую ориентацию, если кратчайший поворот первой оси вокруг их точки пересечения до положения сонаправленности со второй осью осуществляется против часовой стрелки. В противном случае говорят, что эта пара осей имеет левую ориентацию.

Определение. Угол между положительными направлениями координатных осей называется координатным углом.

п.2. Общая и прямоугольная декартовая система координат на плоскости.

Выберем упорядоченную пару неколлинеарных координатных осей на плоскости с общим началом координат, с правой ориентацией, с произвольным координатным углом и с одинаковым масштабом. Первую ось обозначим Ох и назовем её осью абсцисс, вторую – Оу и назовем её осью ординат.

Для каждой точки плоскости определим понятие её координат. Пусть М – произвольная точка плоскости. Проведем через точку М прямые параллельные координатным осям. Точку пересечения построенной прямой с осью Ох обозначаем . Вторую точку пересечения обозначим .

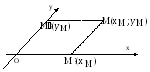
рис.5.

Определение. Точка называется проекцией точки М на ось Ох параллельно оси Оу, а точка называется проекцией точки М на ось Оу параллельно оси Ох.

Каждая точка на координатной оси имеет свою координату. Обозначим через координату точки и назовем её абсциссой точки М. Обозначим через координату точки и назовем её ординатой точки М.

Определение. Координатами точки М на плоскости называют упорядоченную пару действительных чисел , где – абсцисса точки М, а – ордината точки М. Соответственно, ось х называется осью абсцисс, ось у – осью ординат.

Определение. Плоскость, на которой выбраны две неколлинеарные координатные оси с правой ориентацией, с общим началом координат, выбранным масштабом и для каждой точки которой определено понятие её координат, называется координатной плоскостью. Говорят также, что на плоскости введена декартовая система координат.

Определение. Декартовая система координат на плоскости с координатным углом равным называется прямоугольной.

Замечание. В дальнейшем мы будем изучать только прямоугольную декартовую систему координат и сокращенно писать: ПДСК.

п.3. Ориентация трех взаимно перпендикулярных координатных осей в пространстве.

Пусть Ох, Оу и Оz – три взаимно перпендикулярные координатные оси в пространстве с общим началом координат в точке их пересечения О. Назовем ось Ох осью абсцисс, ось Оу – осью ординат, ось Оz – осью аппликат.

В зависимости от выбора направлений на координатных осях возможны 8 случаев. Однако существует только два принципиально различных случая, которые мы и будем рассматривать. А именно, мы будем рассматривать кратчайший поворот оси Ох вокруг начала координат в плоскости Оху к оси Оу. Причем мы будем наблюдать за этим поворотом "сверху", т.е наблюдатель находится в той части полупространства относительно плоскости Оху, в которой находится положительная полуось аппликат.

Если наблюдаемый поворот осуществляется против часовой стрелки (см. рис.6), то говорят, что оси координат имеют правую ориентацию, иначе (см. рис.7), говорят, что оси координат имеют левую ориентацию.

рис.6.

рис.7.

п.4. Прямоугольная декартовая система координат в пространстве.

Пусть Ох, Оу, Оz – три взаимно перпендикулярные оси с правой ориентацией, с общим началом координат О и выбранным масштабом. Введем понятие координат произвольной точки пространства М. Пусть – проекции точки М на координатные оси Ох, Оу, Оz соответственно.

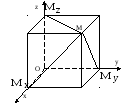
рис.8.

Каждая точка на координатной оси имеет координату. Обозначим координаты точек на координатных осях Ох, Оу, Оz соответственно, т.е. и назовем соответственно абсциссой, ординатой и аппликатой точки М. Общепринято следующее обозначение координат точки М: .

Определение. Прямоугольной декартовой системой координат в пространстве называются три взаимно перпендикулярные оси с правой ориентацией, с общим началом координат, выбранным масштабом и введенным понятием координаты любой точки пространства.

п.5. Декартовые координаты вектора в ПДСК на плоскости и в пространстве.

Мы рассмотрим сразу общий случай координатного пространства. Координатная плоскость будет частным случаем, хотя можно все рассуждения повторить (практически дословно) и для плоскости.

Пусть М – произвольная точка координатного пространства Охуz.

Определение. Вектор называется радиус-вектором точки М.

Введем обозначения:

, , .

Или, для произвольного вектора :

, , .

Определение. Проекции вектора на координатные оси называются его декартовыми координатами.

Теорема. (О координатах точки и ее радиус-вектора.)

Координаты точки М в ПДСК в пространстве совпадают с декартовыми координатами её радиус-вектора.

Доказательство.

рис.9.

По определению, координаты точки М есть координаты точек на координатных осях Ох, Оу, Оz соответственно, т.е. , , . Так как точки М и лежат в плоскости перпендикулярной оси Ох, то . По аналогичной причине и . Отсюда и следуют доказываемые равенства:

, , .

Теорема доказана.

Заметим, что положение точки М в пространстве однозначно определяется ее координатами, т.е. существует взаимно однозначное соответствие между всеми точками пространства и упорядоченными тройками действительных чисел – их координатами. Вследствие этого, координатное пространство обозначают как декартов куб множества действительных чисел: . (Соответственно координатную плоскость как декартов квадрат множества действительных чисел: )

Далее, очевидно, существует биекция и между всеми точками пространства и их радиус-векторами, а значит и между радиус-векторами точек пространства и , т.е

их декартовыми координатами как упорядоченными тройками действительных чисел:

. (1)

В силу этого взаимно однозначного соответствия принято отождествлять радиус-вектор с упорядоченной тройкой его декартовых координат:

.

. (2)

Пусть – произвольный вектор пространства и, отложив его от начала координат, получим . Т.к. проекции вектора на оси не зависят от выбора точки его начала, то можно записать:

, (3)

т.е. существует взаимно однозначное соответствие между всеми векторами пространства и всеми упорядоченными тройками действительных чисел, их декартовыми координатами.

Отсюда сразу же вытекает следующая теорема.

Теорема. (О равенстве векторов.)

Два вектора равны тогда и только тогда, когда равны их декартовые координаты.

Определение. Запись вектора в виде (2) или (3) называется его координатной формой записи.

Теорема. (О действиях с векторами в координатной форме.) При сложении векторов их декартовые координаты складываются, а при умножении вектора на число каждая декартовая координата вектора умножается на это число.

Иначе, пусть , , . Тогда: 1) ;

2) .

Доказательство. Сразу же следует из свойств проекции вектора на ось:

. .

Аналогично доказывается второе утверждение теоремы.

Теорема доказана.

Теорема. (О вычислении декартовых координат вектора.)

Для того, чтобы вычислить декартовые координаты вектора нужно из координат его конца вычесть координаты его начала.

Иначе, пусть и , – координаты его начала и конца. Тогда

(4)

Доказательство. Пусть О(0; 0; 0) – начало координат. Тогда по правилу треугольника сложения векторов

рис.10.

. Векторы и являются радиус-векторами точек А и В соответственно и их декартовые координаты совпадают с координатами этих точек: , . Применяя теорему о действиях с векторами в координатной форме, получаем

.

Теорема доказана.