Головизин_Лекции / Лекция 4. ДСК на прямой

Лекции по алгебре и геометрии. Семестр 1.

Лекция 4. Проекция вектора на ось и декартовая система координат на прямой.

Краткое содержание: угол между векторами, угол между вектором и осью, проекция вектора на ось, определение декартовой координаты вектора оси, теорема Шаля, свойства проекции вектора на ось, координатная форма записи вектора оси, радиус-вектор точки оси, координата точки оси, координатная прямая (числовая ось), вычисление декартовой координаты вектора числовой оси и расстояния между её двумя точками, деление отрезка в данном отношении, деление отрезка внутренним и внешним образом, вычисление отношения, в котором точка делит отрезок, вычисление координаты точки деления отрезка, координаты середины отрезка.

Глава 4. Проекция вектора на ось и декартовая система координат на прямой.

п.1. Угол между векторами. Угол между вектором и осью.

Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.

рис.1.

Обозначение. . Из определения следует, что .

Мы полагаем очевидным, что при параллельном переносе любого из двух векторов угол между ними остается неизменным, только в этом случае поворот одного из векторов осуществляется либо в общей для обоих векторов плоскости, либо в плоскости параллельной другому вектору.

Введем понятие угла между вектором и осью.

Определение. Углом между вектором и осью называется угол между данным вектором и любым правоориентированным вектором этой оси.

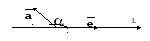
рис.2.

Обозначение. .

п.2. Проекция вектора на ось.

Пусть дан вектор и ось L. Через точки А и В проведем соответственно плоскости и перпендикулярные оси L и точки пересечения оси L с этими плоскостями обозначим соответственно через и . Тогда по определению, точка является проекцией точки А на ось L, а точка – проекция точки В на ось L.

рис.3.

Определение. Проекцией вектора на ось L называется число равное модулю вектора , если он правоориентированный на оси L или противоположное ему число в противном случае. Здесь – проекция точки А на ось L, – проекция точки В на ось L.

Обозначение:

. (1)

Теорема. (О вычислении проекции вектора на ось.)

Проекция вектора на ось не зависит от выбора точки его начала и может быть вычислена по формуле:

(2)

Доказательство.1) Рассмотрим сначала ситуацию, когда вектор отложен от точки А оси L. Здесь возможны два случая, когда угол между данным вектором и данной осью является острым или тупым.

рис.4. рис.5.

В первом случае (рис.4) и по определению проекции вектора на ось

,

где последнее равенство следует из прямоугольного треугольника .

Во втором случае (рис.5) и тогда , ч.т.д.

2) Пусть теперь вектор отложен от произвольной точки А пространства точек S. Найдем проекцию вектора на ось L (см. рис.3). Далее, через точку проведем прямую параллельно прямой АВ и обозначим через С точку её пересечения с плоскостью . Смотри, далее, рисунок 6.

рис.6.

Рассмотрим четырехугольник . Сторона по построению, стороны , как линии пересечения параллельных плоскостей и плоскостью четырехугольника . Таким образом, четырехугольник – параллелограмм и . А так как точка С лежит на плоскости , то точка – проекция точки С на ось L и, следовательно, . Из равенства векторов следует равенство их модулей и равенство углов между этими векторами и осью L, откуда, по уже доказанной в первой части этого доказательства формуле, получаем:

, ч.т.д. Теорема доказана.

п.2. Декартовая координата вектора оси.

Пусть L произвольная ось и . Отложим вектор от какой-нибудь точки . Обозначим через конец вектора .

В А В L

рис.7.

На рис.7 совмещены два возможных случая: и , т.к. вектор может быть правоориентированным на оси L или левоориентированным.

Определение. Декартовой координатой вектора оси называется проекция этого вектора на эту ось.

Обозначим декартовую координату вектора оси L через . Тогда по определению

. (3)

Если , то декартовую координату вектора на оси L будем обозначать

.

Из определения декартовой координаты вектора оси сразу же вытекает следующая теорема.

Теорема. (О знаке декартовой координаты вектора оси.)

Декартовая координата вектора оси неотрицательна и равна его модулю, если вектор правоориентированный на оси. Декартовая координата вектора оси отрицательна и противоположна его модулю, если вектор левоориентированный на оси.

. (4)

Доказательство. Смотрим рисунок 7. Если вектор – правоориентированный на оси L, то угол и

.

Если же вектор – левоориентированный на оси L, то угол и

.

Теорема доказана.

Замечания 1) В дальнейшем, мы часто будем иметь дело с координатными осями Ох, Оу, Оz. В соответствии с этим декартовые координаты вектора на этих осях мы будем обозначать соответственно или .

2) Во многих учебниках аналитической геометрии то, что мы назвали декартовой координатой вектора оси называют величиной вектора оси и часто имеют другие обозначения. Будьте очень внимательны к обозначениям!

Следствие. (О декартовых координатах противоположных векторах оси.)

Пусть – два противоположных друг другу вектора оси L. Тогда .

Доказательство. Из определения противоположных векторов следует, что они имеют равные модули, и на оси противоположно ориентированы. Осталось применить теорему. (См. также формулу (4)).

Следствие доказано.

п.3. Теорема Шаля.

Теорема. (М. Шаль, 1830г.)

Для любых трех точек А, В, С оси L справедливо равенство:

, (5)

где – декартовые координаты векторов оси L соответственно.

Доказательство. 1) Рассмотрим сначала случай, когда точка С находится на отрезке АВ:

рис.8.

В этом случае векторы и правоориентированные и их проекции на ось L равны их модулям, т.е. , и . Т.к. , и , то по свойству функции расстояния .

Отсюда следует равенство и , ч.т.д.

2) Теперь рассмотрим какой-нибудь другой случай расположения точек А, В, С на оси L. См., например, рис.9:

рис.9.

Так как точка А находится на отрезке ВС, то используя только что доказанный случай, имеем равенство: . По следствию о декартовых координатах противоположных векторов , , откуда следует и , ч.т.д.

Аналогично доказываются все оставшиеся случаи расположения точек А, В, С на оси L.

Теорема доказана.

п.4. Свойства проекции вектора на ось.

Теорема. (Свойства проекции.)

Для любых векторов , для любого действительного числа k и любой оси L выполняются равенства:

1) ; 2) .

Коротко оба свойства можно сформулировать так:

Проекция суммы равна сумме проекций и скалярный множитель можно выносить за знак проекции.

Доказательство. 1) Отложим вектор от произвольной точки А и сложим с вектором по правилу треугольника:

рис.10.

Пусть – проекции точек А, В и С на ось L. В каком бы порядке не располагались точки на оси L, по теореме Шаля имеем:

, (6)

где – декартовые координаты векторов на оси L. С другой стороны, по определению декартовой координаты вектора на ось,

, , . Подставляя в (6), получаем . А так как , , , то , ч.т.д.

2) Рассмотрим два случая: а) ; б) .

рис.11. рис.12.

а) Пусть . По теореме о вычислении проекции

вектора на ось и по определению умножения вектора на число .

Отсюда следует (см. рис.11), что и

, ч.т.д.

б) Пусть (см. рис.12). Имеем и . Обозначив , получаем:

, ч.т.д.

Теорема доказана.

Следствие. (О декартовых координатах векторов оси.)

Пусть L – произвольная ось и – произвольные векторы этой оси. Пусть – произвольное действительное число. Тогда:

1) если , то ;

2) если , то .

Другими словами можно сказать, что при сложении векторов оси их декартовые координаты складываются, а при умножении вектора оси на действительное число его декартовая координата умножается на это число.

Доказательство. По определению декартовой координаты вектора

,

, ч.т.д.

Замечание. Нетрудно показать, исходя из определения декартовой координаты вектора оси, что любой вектор оси L однозначно определяется своей декартовой координатой . Другими словами, существует взаимно однозначное соответствие между всеми векторами пространства и полем скаляров R, т.е. , причем это соответствие сохраняет операции сложения и умножения на скаляр (см. следствие о декартовых координатах векторов оси). В современной алгебре, такое соответствие называется изоморфизмом векторных пространств. Это позволяет отождествить вектор оси с его декартовой координатой и писать:

Такая форма записи вектора оси называется координатной.

Отсюда сразу же вытекает следующая теорема.

Теорема. (О равенстве векторов.)

Два вектора равны тогда и только тогда, когда равны их декартовые координаты.

п.5. Числовая (координатная) ось.

Пусть дана произвольная ось. Выберем и зафиксируем на этой оси произвольную точку О, которую будем называть началом координат (точкой отсчета), а саму ось будем обозначать Ох. Пусть А произвольная (текущая) точка оси Ох.

Определение. Вектор , где О – начало координат, называется радиус-вектором точки А и обозначается:

. (7)

Обозначим через декартовую координату радиус-вектора :

.

Определение. Координатой точки А оси Ох называется декартовая координата её радиус-вектора .

Таким образом, из определений координаты точки оси, декартовой координаты вектора оси и проекции вектора на ось следуют равенства:

(8)

Изобразим на оси Ох возможные расположения точки А относительно начала координат.

А О А х

рис.13.

В одном случае, точка А следует за точкой О (радиус-вектор точки А является правоориентированным) и из формулы (8) следует, что

.

В другом, точка А предшествует точке О (радиус-вектор точки А является левоориентированным) и

.

Отложим на оси Ох точку Е с координатой .

О E х

| |

рис.14

Определение. Отрезок ОЕ, где О – начало координат, а координата точки Е равна , называется масштабом на оси L.

Замечание. Выбирая масштаб на оси, мы тем самым задаем функцию расстояния на этой оси.

Определение. Прямая, на которой выбрано положительное направление, начало координат, масштаб и для каждой точки которой определена её координата, называется координатной прямой или числовой осью. Говорят также, что на прямой введена декартовая система координат.

Теорема. Между множеством точек координатной оси Ох и множеством действительных чисел R существует взаимно однозначное соответствие (биекция).

Доказательство. Устроим отображение по правилу: каждой точке поставим в соответствие её координату .

Из определения координаты точки (см. формулу (8)) следует, что каждая точка оси имеет единственную координату. Таким образом, данное правило действительно задает отображение.

Далее, из определения координаты точки следует, что любые две различные точки имеют различные координаты, т.е. данное отображение является инъекцией.

И, наконец, пусть – произвольное действительное число. Отложим на оси Ох вектор с декартовой координатой . Т.к. , то такой вектор существует для любого . Тогда .

Следовательно, любое число является образом некоторой точки при этом отображении, т.е. отображение является сюръекцией. Отображение, которое является одновременно инъекцией и сюръекцией является биекцией, т.е. взаимно однозначным отображением, ч.т.д.

Теорема доказана.

Замечание. В силу только что доказанной теоремы, мы можем отождествить точку числовой оси и число, которое равно ее координате.

Поэтому после буквы обозначающей точку, в круглых скобках пишут ее координату: и т.д.

Определение. Положительной полуосью называется та часть координатной оси, все точки которой имеют положительные координаты (все эти точки следуют за началом координат). Отрицательной полуосью называется та часть координатной оси, все точки которой имеют отрицательные координаты (все эти точки предшествуют началу координат).

п.6. Расстояние между двумя точками на координатной оси и замечание о его обозначении.

Замечание . В геометрии и в школьной геометрии, в частности, принято обозначать одинаково и сам отрезок и его длину. Если имеется отрезок прямой, ограниченный точками А и В, то этот отрезок как геометрический объект обозначается АВ.

рис.15.

С другой стороны длина отрезка, т.е. расстояние между точками А и В обозначается точно также АВ.

Мы же, в нашем курсе, уже встретились с различными обозначениями длины отрезка:

.

Но и это еще не все. Если речь идет об отрезке на оси L, то есть, когда , то длину отрезка АВ мы можем обозначить и так:

.

А если ось мы обозначим другой буквой, например, Ох или Оу, то могут появиться и другие обозначения.

В дальнейшем мы будем стараться придерживаться традиционного обозначения и обозначать длину отрезка АВ также, как и сам отрезок: АВ.

Теорема. (О вычислении декартовой координаты вектора и расстоянии между точками числовой оси.)

Пусть Ох координатная ось, А, В – две её произвольные точки, – их координаты, – декартовая координата вектора . Тогда:

1) ; 2) .

Доказательство. По правилу треугольника сложения векторов имеем:

.

Применяя следствие о декартовых координатах векторов оси, получаем

.

2) Из определения декартовой координаты вектора оси следует, что . Подставляя сюда доказанное уже равенство , получаем .

Теорема доказана.

Замечание. Используя доказанную теорему, можно сформулировать два правила:

1) Для того, чтобы найти координату вектора на числовой оси, нужно из координаты его конца вычесть координату его начала.

2) Расстояние между двумя точками числовой оси равно модулю разности их координат.

п.7. Деление отрезка в данном отношении.

Определение. Пусть L – произвольная прямая, – её произвольные точки, причем . Говорят, что точка С делит отрезок АВ, считая от точки А, в отношении , если .