
Головизин_Лекции / Лекция 15. Эллипс
.docЛекции по алгебре и геометрии. Семестр 1.
Лекция 15. Эллипс.
Краткое содержание: определение эллипса, основная терминология, каноническая для эллипса система координат и каноническое уравнение эллипса, параметрические уравнения эллипса, эллипс как результат сжатия окружности, касательная к эллипсу, зеркальное свойство эллипса, директрисы и фокальный параметр эллипса, второе определение эллипса.
Глава 15. Эллипс.
п.1. Основные определения.
Определение. Эллипсом называется ГМТ плоскости сумма расстояний которых до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная.

рис.1.
Определение. Расстояние от произвольной точки М плоскости до фокуса эллипса называется фокальным радиусом точки М.
Обозначения:
![]() – фокусы эллипса,
– фокусы эллипса,
![]() – фокальные радиусы точки М.
– фокальные радиусы точки М.
По
определению эллипса, точка М является
точкой эллипса тогда и только тогда,
когда
![]() – постоянная величина. Эту постоянную
принято обозначать 2а:
– постоянная величина. Эту постоянную
принято обозначать 2а:
![]() .
(1)
.
(1)
Заметим,
что
![]() .
.
По определению эллипса, его фокусы есть фиксированные точки, поэтому расстояние между ними есть также величина постоянная для данного эллипса.
Определение. Расстояние между фокусами эллипса называется фокусным расстоянием.
Обозначение:
![]() .
.
Из
треугольника
![]() следует, что
следует, что
![]() ,
т.е.
,
т.е.
![]() .
.
Обозначим
через b число равное
![]() ,
т.е.
,
т.е.
![]() .
(2)
.
(2)
Определение. Отношение
![]() (3)
(3)
называется эксцентриситетом эллипса.
Введем на данной плоскости систему координат, которую мы будем называть канонической для эллипса.
Определение. Ось, на которой лежат фокусы эллипса, называется фокальной осью.
Построим каноническую для эллипса ПДСК, см. рис.2.
В
качестве оси абсцисс выбираем фокальную
ось, а ось ординат проводим через середину
отрезка
![]() перпендикулярно фокальной оси.
перпендикулярно фокальной оси.

рис.2.
Тогда
фокусы имеют координаты
![]() ,
,
![]() .
.
п.2. Каноническое уравнение эллипса.
Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:
![]() .
(4)
.
(4)
Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любое решение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и из определения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.
1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:
![]() .
.
Воспользуемся формулой расстояния между двумя точками на координатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:
![]() ,
,
![]() ,
откуда получаем:
,
откуда получаем:
![]() .
.
Перенесем один корень в правую часть равенства и возведем в квадрат:
![]() .
.
Сокращая, получаем:
![]() .
.
Приводим подобные, сокращаем на 4 и уединяем радикал:
![]() .
.
Возводим в квадрат
![]() .
.
Раскрываем
скобки и сокращаем на
![]() :
:
![]() ,
,
откуда получаем:
![]() .
.
Используя равенство (2), получаем:
![]() .
.
Разделив
последнее равенство на
![]() ,
получаем равенство (4), ч.т.д.
,
получаем равенство (4), ч.т.д.
2) Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х, у) – соответствующая точка на координатной плоскости Оху.
Тогда из (4) следует:
![]() .
.
Подставляем это равенство в выражение для фокальных радиусов точки М:
![]()

![]() .
.
Здесь мы воспользовались равенством (2) и (3).
Таким
образом,
![]() .
Аналогично,
.
Аналогично,
![]() .
.
Теперь заметим, что из равенства (4) следует, что
![]() или
или
![]() и т.к.
и т.к.
![]() ,
то отсюда следует неравенство:
,
то отсюда следует неравенство:
![]() .
.
Отсюда, в свою очередь, следует, что
![]() или
или
![]() и
и
![]() ,
,
![]() .
(5)
.
(5)
Из
равенств (5) следует, что
![]() ,
т.е. точка М(х, у) является точкой эллипса,
ч.т.д.
,
т.е. точка М(х, у) является точкой эллипса,
ч.т.д.
Теорема доказана.
Определение. Уравнение (4) называется каноническим уравнением эллипса.
Определение. Канонические для эллипса оси координат называются главными осями эллипса.
Определение. Начало канонической для эллипса системы координат называется центром эллипса.
п.3. Свойства эллипса.
Теорема. (Свойства эллипса.)
1. В канонической для эллипса системе координат, все
точки эллипса находятся в прямоугольнике
![]() ,
,
![]() .
.
2.
Точки
![]() лежат на
лежат на
эллипсе.
3. Эллипс является кривой, симметричной относительно
своих главных осей.
4. Центр эллипса является его центром симметрии.
Доказательство. 1, 2) Сразу же следует из канонического уравнения эллипса.
3,
4) Пусть М(х, у) – произвольная точка
эллипса. Тогда ее координаты удовлетворяют
уравнению (4). Но тогда координаты точек
![]() также удовлетворяют уравнению (4), и,
следовательно, являются точками эллипса,
откуда и следуют утверждения теоремы.
также удовлетворяют уравнению (4), и,
следовательно, являются точками эллипса,
откуда и следуют утверждения теоремы.
Теорема доказана.
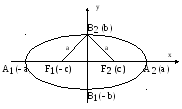
рис.3.
Определение. Величина 2а называется большой осью эллипса, величина а называется большой полуосью эллипса.
Определение. Величина 2b называется малой осью эллипса, величина b называется малой полуосью эллипса.
Определение. Точки пересечения эллипса с его главными осями называются вершинами эллипса.
Замечание.
Эллипс можно построить следующим
образом. На плоскости в фокусы "забиваем
по гвоздю" и закрепляем на них нить
длиной
![]() .
Затем берем карандаш и с его помощью
натягиваем нить. Затем передвигаем
карандашный грифель по плоскости, следя
за тем, чтобы нить была в натянутом
состоянии.
.
Затем берем карандаш и с его помощью
натягиваем нить. Затем передвигаем
карандашный грифель по плоскости, следя
за тем, чтобы нить была в натянутом
состоянии.
Из определения эксцентриситета следует, что
![]()
Зафиксируем число
а и устремим число с к нулю. Тогда при
![]() ,
,
![]() и
и
![]() .
В пределе мы получаем
.
В пределе мы получаем
![]() или
или
![]() – уравнение окружности.
– уравнение окружности.
Таким образом, мы можем считать, что окружность есть эллипс с нулевым эксцентриситетом.
Устремим теперь
![]() .
Тогда
.
Тогда
![]() ,
,
![]() и мы видим, что в пределе эллипс вырождается
в отрезок прямой
и мы видим, что в пределе эллипс вырождается
в отрезок прямой
![]() в обозначениях рисунка 3.
в обозначениях рисунка 3.
п.4. Параметрические уравнения эллипса.
Теорема.
Пусть
![]() – произвольные действительные числа.
Тогда система уравнения
– произвольные действительные числа.
Тогда система уравнения
![]() ,
,
![]() (6)
(6)
является параметрическими уравнениями эллипса в канонических для эллипса системе координат.
Доказательство. Достаточно доказать, что система уравнений (6) равносильна уравнению (4), т.е. они имеют одно и то же множество решений.
1) Пусть (х, у) – произвольное решение системы (6). Разделим первое уравнение на а, второе – на b, возводим оба уравнения в квадрат и складываем:
 .
.
Т.е. любое решение (х, у) системы (6) удовлетворяет уравнению (4).
2) Обратно, пусть пара (х, у) является решением уравнения (4), т.е.
![]() .
.
Из
этого равенства следует, что точка с
координатами
![]() лежит на окружности единичного радиуса
с центром в начале координат, т.е. является
точкой тригонометрической окружности,
которой соответствует некоторый угол
лежит на окружности единичного радиуса
с центром в начале координат, т.е. является
точкой тригонометрической окружности,
которой соответствует некоторый угол
![]() :
:
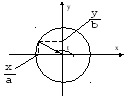
рис.4.
Из определения синуса и косинуса сразу же следует, что
![]() ,
,
![]() ,
где
,
где
![]() ,
откуда и следует, что пара (х, у) является
решением системы (6), ч.т.д.
,
откуда и следует, что пара (х, у) является
решением системы (6), ч.т.д.
Теорема доказана.
Замечание. Эллипс можно получить в результате равномерного "сжатия" окружности радиуса а к оси абсцисс.
Пусть
![]() – уравнение окружности с центром в
начале координат. "Сжатие" окружности
к оси абсцисс есть ни что иное, как
преобразование координатной плоскости,
осуществляемое по следующему правилу.
Каждой точке М(х, у) поставим в соответствие
точку этой же плоскости
– уравнение окружности с центром в
начале координат. "Сжатие" окружности
к оси абсцисс есть ни что иное, как
преобразование координатной плоскости,
осуществляемое по следующему правилу.
Каждой точке М(х, у) поставим в соответствие
точку этой же плоскости
![]() ,
где
,
где
![]() ,
,
![]() – коэффициент "сжатия".
– коэффициент "сжатия".
рис.5.
При этом преобразовании каждая точка окружности "переходит" в другую точку плоскости, имеющую ту же самую абсциссу, но меньшую ординату. Выразим старую ординату точки через новую:
![]()
и подставим в уравнение окружности:
![]() .
.
Отсюда получаем:
![]() .
(7)
.
(7)
Отсюда
следует, что если до преобразования
"сжатия" точка М(х, у) лежала на
окружности, т.е. ее координаты удовлетворяли
уравнению окружности, то после
преображования "сжатия" эта точка
"перешла" в точку
![]() ,
координаты которой удовлетворяют
уравнению эллипса (7). Если мы хотим
получить уравнение эллипса с малой
полуосью b, то нужно взять
коэффициент сжатия
,
координаты которой удовлетворяют
уравнению эллипса (7). Если мы хотим
получить уравнение эллипса с малой
полуосью b, то нужно взять
коэффициент сжатия
![]() .
.

рис.6.
п.5. Касательная к эллипсу.
Теорема.
Пусть
![]() – произвольная точка эллипса
– произвольная точка эллипса
![]() .
.
Тогда
уравнение касательной к этому эллипсу
в точке
![]() имеет вид:
имеет вид:
![]() .
(8)
.
(8)
Доказательство.
Достаточно рассмотреть случай, когда
точка касания лежит в первой или второй
четверти координатной плоскости:
![]() .
Уравнение эллипса в верхней полуплоскости
имеет вид:
.
Уравнение эллипса в верхней полуплоскости
имеет вид:
![]() .
(9)
.
(9)
Воспользуемся
уравнением касательной к графику функции
![]() в точке
в точке
![]() :
:
![]() ,
(10)
,
(10)
где
![]() – значение производной данной функции
в точке
– значение производной данной функции
в точке
![]() .
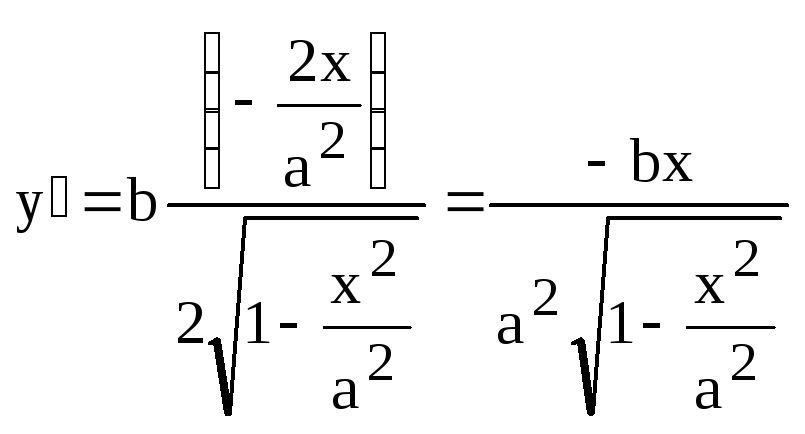
Эллипс в первой четверти можно
рассматривать как график функции (8).
Найдем ее производную и ее значение в
точке касания:
.
Эллипс в первой четверти можно
рассматривать как график функции (8).
Найдем ее производную и ее значение в
точке касания:
 ,
,
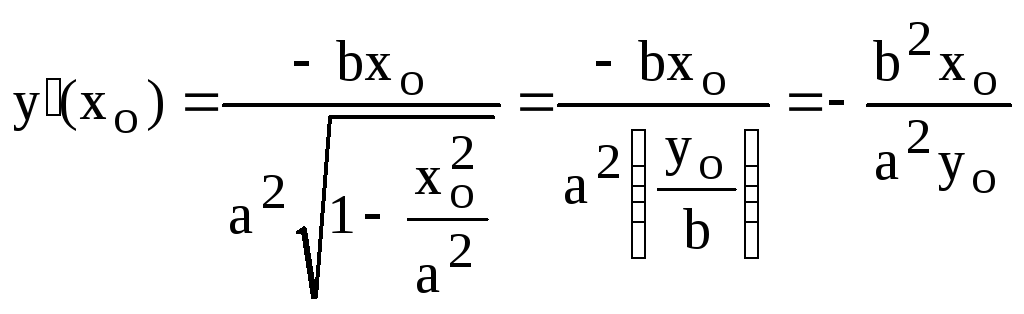 .
Здесь мы воспользовались тем, что точка
касания
.
Здесь мы воспользовались тем, что точка
касания
![]() является точкой эллипса и поэтому ее
координаты удовлетворяют уравнению
эллипса (9), т.е.
является точкой эллипса и поэтому ее
координаты удовлетворяют уравнению
эллипса (9), т.е.
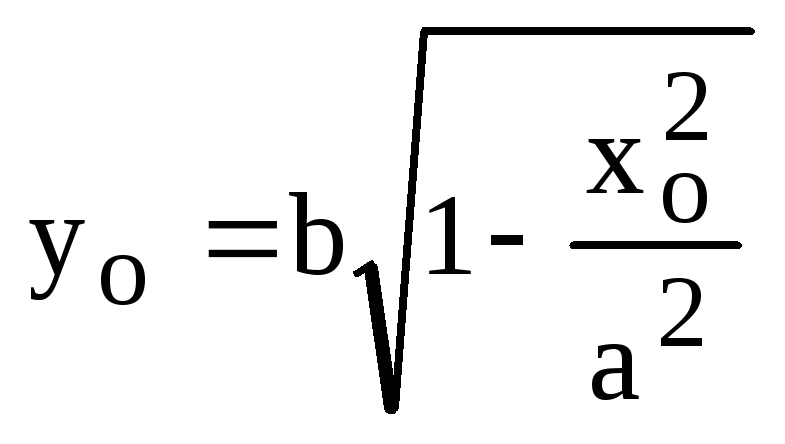 .
.
Подставляем найденное значение производной в уравнение касательной (10):
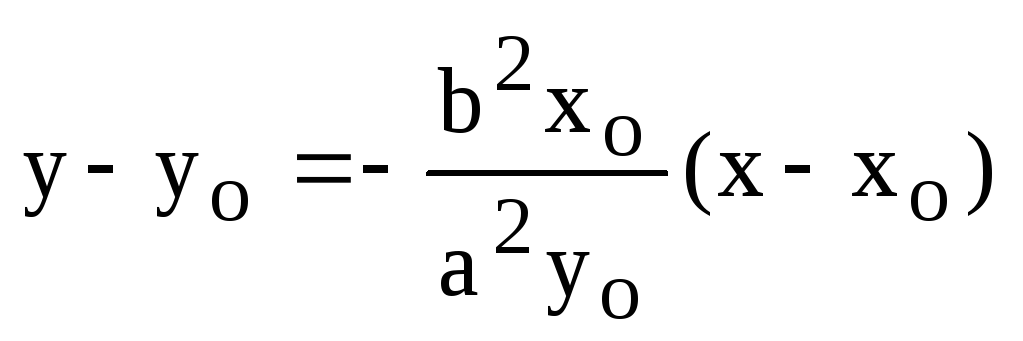 ,
,
откуда получаем:
![]()
или
![]() .
.
Отсюда следует:
![]() .
.
Разделим
это равенство на
![]() :
:
![]() .
.
Осталось
заметить, что
![]() ,
т.к. точка
,
т.к. точка
![]() принадлежит эллипсу и ее координаты
удовлетворяют его уравнению.
принадлежит эллипсу и ее координаты
удовлетворяют его уравнению.
Аналогично доказывается уравнение касательной (8) в точке касания, лежащей в третьей или четвертой четверти координатной плоскости.
И,
наконец, легко убеждаемся, что уравнение
(8) дает уравнение касательной в точках
![]() ,
,
![]() :
:
![]() или
или
![]() ,
и
,
и
![]() или
или
![]() .
.
Теорема доказана.
п.6. Зеркальное свойство эллипса.
Теорема. Касательная к эллипсу имеет равные углы с фокальными радиусами точки касания.

рис.7.
Пусть
![]() – точка касания,
– точка касания,
![]() ,
,
![]() – фокальные радиусы точки касания, Р и
Q – проекции фокусов на
касательную, проведенную к эллипсу в
точке
– фокальные радиусы точки касания, Р и
Q – проекции фокусов на
касательную, проведенную к эллипсу в
точке
![]() .
.
Теорема утверждает, что
![]() .
(11)
.
(11)
Это равенство можно интерпретировать как равенство углов падения и отражения луча света от эллипса, выпущенного из его фокуса. Это свойство получило название зеркального свойства эллипса:
Луч света, выпущенный из фокуса эллипса, после отражения от зеркала эллипса проходит через другой фокус эллипса.
Доказательство
теоремы. Для доказательства равенства
углов (11) мы докажем подобие треугольников
![]() и
и
![]() ,
в которых стороны
,
в которых стороны
![]() и
и
![]() будут сходственными. Так как треугольники
прямоугольные, то достаточно доказать
равенство
будут сходственными. Так как треугольники
прямоугольные, то достаточно доказать
равенство
![]() .
(12)
.
(12)
Так
как по построению
![]() – расстояние от фокуса
– расстояние от фокуса
![]() до касательной L (см.
рис.7),
до касательной L (см.
рис.7),
![]() .
Воспользуемся формулой расстояния от
точки до прямой на плоскости:
.
Воспользуемся формулой расстояния от
точки до прямой на плоскости:
![]() .
.
Так
как уравнение касательной к эллипсу в
точке
![]() имеет вид
имеет вид
![]() ,
,
то
 ,
,
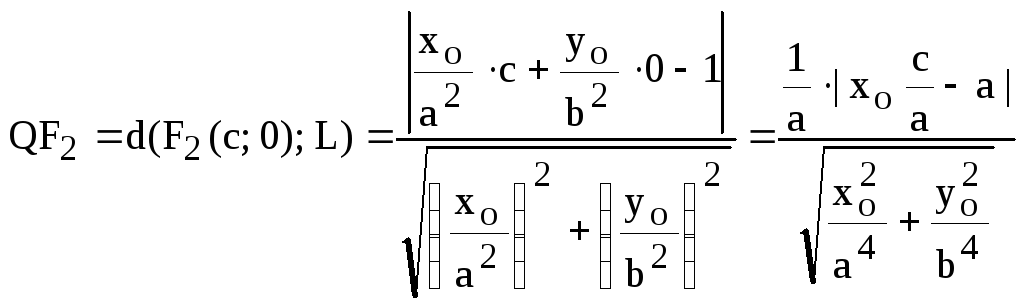
и
![]() .
.
Здесь мы воспользовались формулами (5) для фокальных радиусов точки эллипса.
Теорема доказана.
Второе доказательство теоремы:
![]() ,
,
![]() ,
,
![]() – нормальный вектор касательной L.
– нормальный вектор касательной L.
![]()
![]() .
Отсюда,
.
Отсюда,
![]() .
.
Аналогично
находим,
![]() и
и
![]() ,
ч.т.д.
,
ч.т.д.
п.7. Директрисы эллипса.
Определение. Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения
![]() или
или
![]() .
(13)
.
(13)
рис.8.
Теорема.
Пусть М – произвольная точка эллипса,
![]() ,
,
![]() – ее фокальные радиусы,
– ее фокальные радиусы,
![]() – расстояние от точки М до левой
директрисы,
– расстояние от точки М до левой
директрисы,
![]() – до правой. Тогда
– до правой. Тогда
![]() ,
(14)
,
(14)
где
![]() – эксцентриситет эллипса.
– эксцентриситет эллипса.
Доказательство.
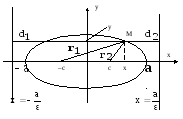
рис.9.
Пусть М(х, у) – координаты произвольной точки эллипса. Тогда
![]() ,
,
![]() ,
,
откуда и следуют равенства (14).
Теорема доказана.
п.8. Фокальный параметр эллипса.
Определение. Фокальным параметром эллипса называется длина перпендикуляра, восстановленного в его фокусе до пересечения с эллипсом.
Фокальный параметр принято обозначать буквой р.
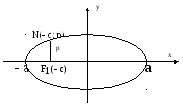
рис.9.
Из определения следует, что фокальный параметр
![]() .
.
Теорема. Фокальный параметр эллипса равен
![]() .
(15)
.
(15)
Доказательство.
Так как точка N(–с; р)
явяляется точкой эллипса
![]() ,
то ее координаты удовлетворяют его
уравнению:
,
то ее координаты удовлетворяют его
уравнению:
![]() .
.
Отсюда находим
![]() ,
,
откуда и следует (15).
Теорема доказана.
п.9. Второе определение эллипса.
Теорема из п.7. может служить определением эллипса.
Определение. Эллипсом называется ГМТ для которых отношение расстояния до фиксированной точки плоскости, называемой фокусом, к расстоянию до фиксированной прямой, называемой директрисой, есть величина постоянная меньше единицы и называемая его эксцентриситетом:
![]() .
.

рис.10.
Разумеется, в этом случае, первое определение эооипса является теоремой, которую необходимо доказывать.
