Головизин_Лекции / Лекция 11. Уравнение прямой

Лекции по алгебре и геометрии. Семестр 1.

Лекция 11. Уравнение прямой.

Краткое содержание: понятие об уравнении линии и поверхности, линия и поверхность как ГМТ, параметрические уравнения, примеры, цилиндрические поверхности, параметрические и канонические уравнения прямой на координатной плоскости и в пространстве, канонические уравнения прямой проходящей через две точки, угол между прямыми, необходимые и достаточные условия параллельности и перпендикулярности двух прямых, взаимное расположение двух прямых на плоскости и в пространстве.

Глава 11. Уравнение прямой.

п.1. Понятие об уравнении линии и поверхности.

С теоретико-множественной точки зрения, любая линия или поверхность есть множество точек. Каждое такое множество может обладать некоторыми свойствами. Математики с древних времен пытались отыскать такие свойства, которые полностью определяли бы такие интуитивно понятные объекты как прямая, кривая, поверхность. Эта задача была окончательно решена лишь в двадцатом веке, когда было введено понятие размерности множества. Популярно об этом можно прочитать в замечательной книжке Виленкина Н.Я. "Рассказы о множествах."

Мы же ограничимся интуитивным пониманием линии и поверхности, причем мы полагаем, что и линия и поверхность состоят из точек пространства точек , т.е. являются его подмножествами.

Пусть в пространстве введена ПДСК Охуz и пусть дана некоторая числовая функция трех действительных аргументов . Каждая точка М пространства имеет три координаты: . Если подставить координаты точки М в данную числовую функцию, то мы получаем некоторое числовое значение этой функции.

Определение. Пусть W некоторое подмножество множества точек координатного пространства Охуz. Уравнение

(1)

называется уравнением множества W, если координаты каждой точки множества W удовлетворяет уравнению (1) и, наоборот, каждое решение уравнения (1) определяет координаты точки, лежащей именно в множестве W, т.е.

. (2)

Часто бывает, что одного уравнения (1) не хватает для того чтобы описать данное множество точек (линию или поверхность) и тогда уравнениями данного множества точек называют систему таких уравнений:

. (3)

В аналитической геометрии существует два подхода при изучении линий и поверхностей. Первый подход заключается в том, что изначально имеется уравнение или система уравнений и изучается множество их решений, причем каждое решение рассматривается как координаты точки.

Образует ли какую-нибудь геометрическую форму такое множество решений? Может это какая-нибудь линия или поверхность?

Чтобы предметно и конкретно обсуждать этот вопрос нам понадобятся несколько определений.

Определение. Пусть – многочлен от трех переменных n-й степени. Тогда уравнение называется алгебраическим уравнением n-й степени с тремя неизвестными. Если это уравнение является уравнением кривой (поверхности), то такая кривая (поверхность) называется алгебраической кривой (поверхностью) n-го порядка.

Пример. Уравнение

– алгебраическое уравнение первой степени с одним неизвестным. Однако, мы можем рассматривать это уравнение как уравнение с тремя неизвестными х, у и z. Тогда множество всех решений этого уравнения есть множество

.

Рассматривая это множество Р как множество точек в координатном пространстве Охуz, мы находим, что данному уравнению удовлетворяют координаты всех точек плоскости, параллельной координатной плоскости Оуz, отстоящей от нее на расстоянии 2 и проходящей через точку (2, 0, 0) и только они. Следовательно, данное уравнение является уравнением плоскости и эта плоскость является алгебраической поверхностью первого порядка.

Мы можем рассматривать данное уравнение как уравнение с двумя неизвестными х и у. Тогда множество всех решений этого уравнения есть множество

.

Рассматривая это множество L как множество точек на координатной плоскости Оху, мы находим, что данному уравнению удовлетворяют все точки прямой линии, параллельной координатной оси Оу, отстоящей от нее на расстоянии 2 и проходящая через точку (2, 0) и только они. Следовательно, данное уравнение является уравнением прямой, лежащей на координатной плоскости Оху и эта прямая является алгебраической линией первого порядка.

Определение. Уравнение, содержащее трансцендентные функции (тригонометрические, показательные, логарифмические), называется трансцендентными.

Пример. Рассмотрим систему уравнений

, (4)

Будем рассматривать множество решений (х, у) этой системы как координаты точек на координатной плоскости Оху. Нетрудно доказать, что множество решений (х, у) системы (4) совпадает на координатной плоскости Оху с окружностью радиуса R с центром в начале координат. Т.е. для любого , пара чисел (х, у) определяет координаты точки, лежащей на указанной окружности и наоборот, взяв координаты любой точки, лежащей на этой окружности и подставив их в уравнения (4), получим два верных числовых равенства для некоторого числа . Это означает, что система (4) является уравнением окружности.

Определение. Система уравнений вида

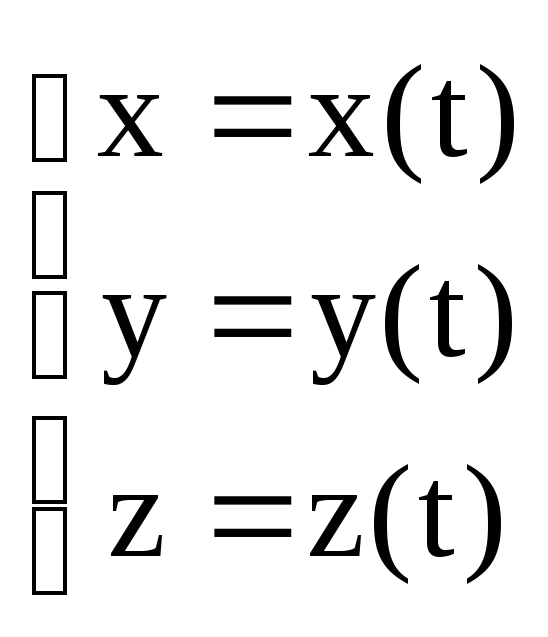, (5),

где – некоторые числовые функции от одной переменной t, называется параметрическими уравнениями кривой (линии) L, а переменная t называется параметром, если система (5) устанавливает взаимно однозначное соответствие между всеми точками и всеми значениями параметра .

Так система уравнений (4) называется параметрическим уравнениями окружности. Следующая система уравнений называется параметрическими уравнениями винтовой линии:

, .

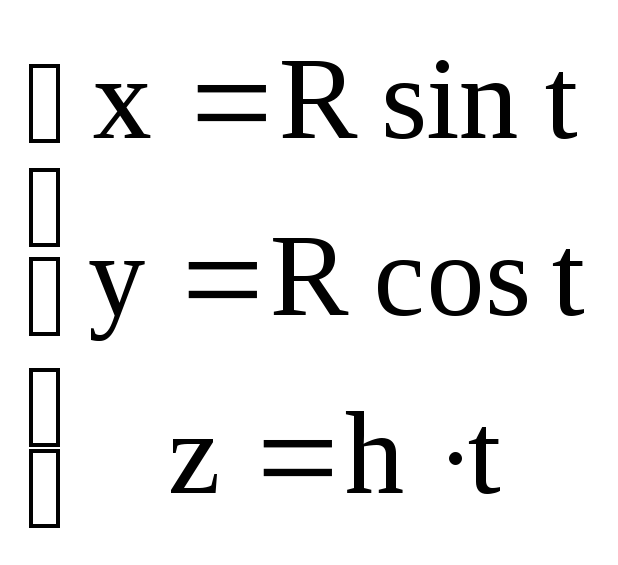Второй подход при изучении линий и поверхностей заключается в том, что изначально мы имеем некоторую линию или поверхность, которая задаются каким либо своим геометрическим свойством. Очень часто линия или поверхность определяется как множество точек координатной плоскости или координатного пространства, удовлетворяющих каким-либо условиям. Такое множество точек называется геометрическим местом точек (сокращенно ГМТ). Задача заключается в том, чтобы описать это ГМТ с помощью уравнения или системы уравнений с параметром или без такового.

Пример. Найти уравнение ГМТ координатной плоскости Оху, равноудаленных от начала координат на расстоянии, равном R.

Решение. Из геометрии нам известно, что такое ГМТ образует окружность радиуса R с центром в начале координат. Наша задача найти уравнение окружности, используя ее определяющее свойство – равноудаленность всех ее точек от центра.

Пусть М(х, у) – произвольная точка этого ГМТ. Тогда . С другой стороны, длина отрезка ОМ может быть найдена по формуле . Отсюда,

или

. (6)

Таким образом, координаты любой точки окружности удовлетворяют уравнению (6). С другой стороны, если точка М(х, у) не принадлежит окружности, то длина отрезка ОМ не равна R и ее координаты не удовлетворяют уравнению (6). Следовательно, уравнению (6) удовлетворяют координаты только тех точек, которые лежат на окружности и только они. Поэтому уравнение (6) является уравнением указанной окружности.

Ответ: .

Аналогично можно найти уравнение сферы:

.

Замечание. Из последних двух примеров следует, что окружность является алгебраической кривой 2-го порядка, а сфера является алгебраической поверхностью 2-го порядка.

Пример. Найти уравнение ГМТ плоскости, равноудаленных от координатных осей.

Решение. Очевидно, таким уравнением будет уравнение

или совокупность двух уравнений прямых:

.

Пример. Найти уравнение траектории точки окружности радиуса R, катящейся по прямой (без скольжения и пробуксовки). Такая линия называется циклоидой.

Ответ: (без доказательства).

,

– параметрические уравнения циклоиды (трансцендентные);

– уравнение циклоиды (трансцендентное).

Таким образом, мы видим, что циклоида является примером трансцендентной кривой.

Замечание. Циклоидой будет траектория жвачки, если вы ее налепите на колесо вашего автомобиля, а потом поедете по прямой дороге (разумеется не в гололед и по хорошей дороге, например, по автобану).

Определение. Плоской кривой называется кривая, лежащая в одной плоскости.

Окружность, парабола, циклоида являются примерами плоских кривых. Винтовая линия предоставляет нам пример не плоской кривой.

Уже из приведенных здесь примеров мы видим, что одна и та же кривая может быть описана различными уравнениями. Одна из задач геометрии заключается в том, чтобы параметризовать известную кривую, т.е. найти параметрические уравнения кривой, удобные для дальнейшей работы с этой кривой. Далеко не всякая параметризация бывает удобной. Например, если кривая на плоскости Оху описывается уравнением , то тривиальной ее параметризацией является следующая:

, , где D – область изменения аргумента х.

В дальнейшем, мы очень подробно рассмотрим все виды уравнений прямой на координатной плоскости, уравнения плоскостей и прямых в пространстве. Далее в наших планах изучение алгебраических кривых и поверхностей второго порядка, т.е. кривых и поверхностей, которые описываются алгебраическими уравнениями второй степени, соответственно, с двумя или тремя неизвестными.

п.2. Цилиндрические поверхности.

Определение. Поверхность называется цилиндрической, если она образована параллельным перемещением некоторой прямой, называемой образующей, вдоль некоторой кривой, называемой направляющей.

Пример. Возьмем в качестве направляющей окружность. Рассмотрим множество прямых параллельных друг другу и расположенных под некоторым углом к плоскости в которой лежит окружность и проходящих через каждую точку окружности.

рис.1.

Поверхность, изображенная на рис.1. является цилиндрической. Она может быть получена параллельным перемещением одной прямой (образующей) вдоль окружности (направляющей). Если угол наклона прямой к плоскости направляющей является прямым, то получаем поверхность, которая называется прямым круговым цилиндром.

Не нужно думать, что образующая должна быть замкнутой кривой. Это вовсе не обязательно. См., например, следующий рисунок.

K

рис.2.

Здесь K – направляющая, L – образующая цилиндрической поверхности.

В частности, плоскость является цилиндрической поверхностью, т.к. может быть получена параллельным перемещением прямой (образующей) вдоль другой прямой, которая служит направляющей.

Теорема. Если уравнение является уравнением кривой на координатной плоскости Оху, то это же уравнение является уравнением цилиндрической поверхности, направляющей которой служит данная кривая, а образующей является прямая, проходящая через точку данной кривой и параллельной оси Оz.

Доказательство. Пусть точка лежит на кривой . Тогда . Так как это уравнение не содержит переменной z, то для любого числа координаты точки также удовлетворяют этому уравнению. Иначе, любое решение этого уравнения есть координаты точки, лежащей на прямой, параллельной оси Оz и проходящей через точку кривой на плоскости Оху. Очевидно, верно и обратное.

рис.3.

Теорема доказана.

Аналогично, уравнение кривой на плоскости Охz является одновременно и уравнением цилиндрической поверхности, направляющей для которой служит данная кривая, а образующая параллельна оси ординат. Так же и уравнение есть уравнение цилиндрической поверхности, образующая которой параллельна оси Ох.

Пример. Изобразить в ПДСК Охуz тело, лежащее в первом октанте, ограниченное координатными плоскостями, плоскостью и прямым круговым цилиндром .

Решение.

рис.4.

п.3. Параметрические и канонические уравнения прямой.

Определение. Любой ненулевой вектор, коллинеарный данной прямой называется ее направляющим вектором.

Пусть L – произвольная прямая и – ее произвольная, но фиксированная точка, О – начало координат, – произвольная (текущая) точка прямой L, – радиус вектор точки , – радиус вектор текущей точки М, – произвольный направляющий вектор прямой L.

рис.5.

Теорема. Следующая система уравнений является параметрическими уравнениями прямой:

, , (7)

где – координаты произвольной фиксированной точки данной прямой, – соответствующие координаты произвольного направляющего вектора данной прямой, t – параметр.

Доказательство. В соответствии с определением уравнения любого множества точек координатного пространства, мы должны доказать, что уравнениям (7) удовлетворяют все точки прямой L и, с другой стороны, не удовлетворяют координаты точки не лежащей на прямой.

Пусть произвольная точка . Тогда векторы и являются по определению коллинеарными и по теореме о коллинеарности двух векторов следует, что один из них линейно выражается через другой, т.е. найдется такое число , что . Из равенства векторов и следует равенство их координат:

, , , ч.т.д.

Обратно, пусть точка . Тогда и по теореме о коллинеарности векторов ни один из них не может быть линейно выражен через другой, т.е. и хотя бы одно из равенств (7) не выполняется. Таким образом, уравнениям (7) удовлетворяют координаты только тех точек, которые лежат на прямой L и только они, ч.т.д.

Теорема доказана.

Следствие. Следующая система уравнений является уравнениями прямой:

. (8)

Доказательство. Выразив параметр t из уравнений (7), получаем:

, , , (9)

откуда и следуют уравнения (8). Ясно, что системы уравнений (7) и (8) равносильны, т.е. их множества решений совпадают и система (8), так же как и система (7), являются уравнениями прямой, ч.т.д.

Следствие доказано.

Определение. Уравнения (8) называются каноническими уравнениями прямой.

Замечание. Уравнения (8) отражают факт коллинеарности векторов . Два вектора коллинеарные тогда и только тогда, когда их координаты пропорциональны. При этом, одна или две координаты направляющего вектора прямой могут быть равны нулю и в канонических уравнения прямой нули появляются в знаменателе. Это лишь означает, как это следует из уравнений (7), что числитель такой дроби тоже равен нулю, т.е. равны нулю соответствующие координаты коллинеарных векторов.

Заметим также, что модуль направляющего вектора задает масштаб на прямой L, а его направление задает на прямой L положительное направление.

Иначе говоря, задание направляющего вектора прямой определяет на этой прямой ДСК, т.е превращает ее в числовую прямую с началом координат в точке , которая соответствует значению . Числовая координата t произвольной точки М этой оси определяется из равенств (9). И наоборот, любое числовое значение t определяет с помощью уравнений (7) точку на этой прямой .

п.4. Решение некоторых задач аналитической геометрии на прямую в пространстве и на плоскости.

Задача 1. Найти уравнение прямой, проходящей через две различные точки и .

Решение. Вектор

,

очевидно, является направляющим вектором прямой, которая проходит через эти точки. В уравнениях (8) есть координаты произвольной фиксированной точки данной прямой, поэтому в качестве такой точки можно взять точку или , без разницы которую.

Подставляя в уравнения (8) координаты точки и координаты направляющего вектора получаем уравнение прямой, проходящей через две заданные точки:

. (10)

Задача 2. Найти угол между прямыми

и .

Решение. Из канонических уравнений прямых находим их направляющие векторы и . Тогда искомый угол равен либо углу между их направляющими векторами

,

где – скалярное произведение векторов, либо равен

.

Следствие. (Условия параллельности и перпендикулярности двух прямых.)

1. Две прямые параллельны или совпадают тогда и только тогда, когда их направляющие векторы коллинеарные:

.

2. Две прямые перпендикулярны тогда и только тогда, когда их направляющие векторы ортогональны:

.

Доказательство очевидно.

Задача 3. Определить взаимное расположение двух прямых

и .

Решение.

Две прямые в пространстве могут совпадать, быть параллельными, пересекаться в одной точке или быть скрещивающимися.

1) Если , т.е если , то прямые либо совпадают: , либо параллельны: . Определить, какой из этих двух случаев имеет место быть, очень просто. Если точка лежит и на прямой , т.е. ее координаты удовлетворяет уравнениям прямой : , то прямые совпадают. В противном случае прямые параллельны.

2) Если , то прямые либо скрещиваются, либо пересекаются. Если прямые пересекаются, то обе они лежат в одной плоскости и, следовательно, векторы компланарные, в противном случае, т.е. когда прямые скрещиваются, векторы не компланарные. Используя смешанное произведение векторов, получаем:

а) прямые пересекаются в одной точке тогда и только тогда, когда ;

б) прямые скрещиваются тогда и только тогда, когда .

Ответ:

1) прямые совпадают , т.е.

и ;

2) прямые параллельны , т.е.

и

не выполняется хотя бы одно из равенств

;

3) прямые пересекаются в одной точке

, т.е.

хотя бы одно из равенств не выполняется и

;

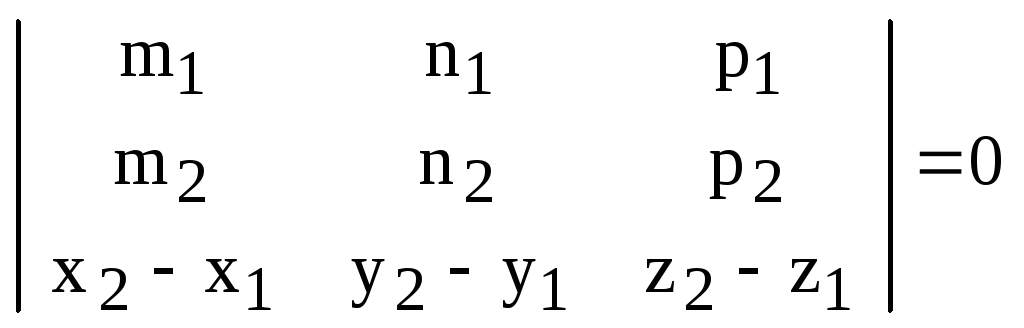4) прямые скрещиваются , т.е.

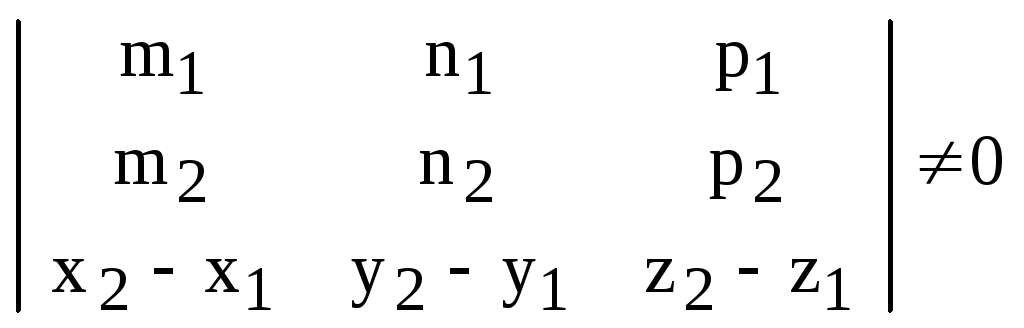. (11)

Замечание. Эту же задачу можно решить следующим образом.

Теорема (О взаимном расположении двух прямых в пространстве.)

Пусть

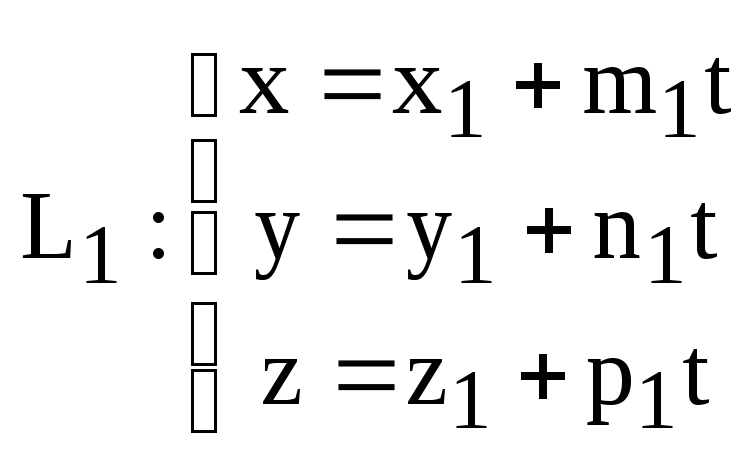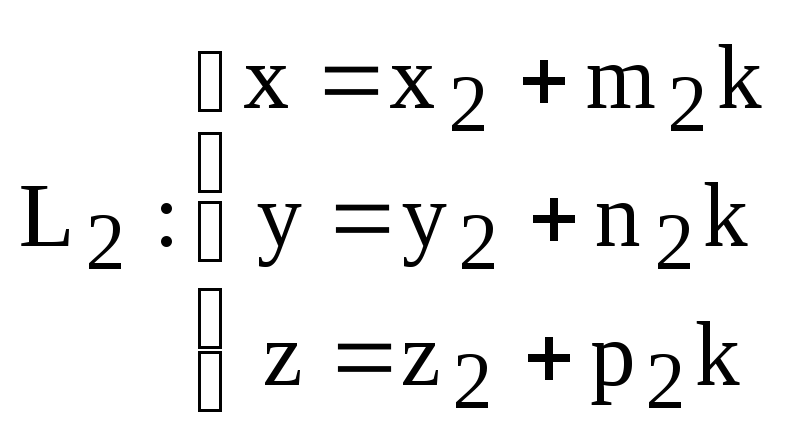и , где

– две произвольные прямые в пространстве и

. (12)

Тогда:

1) если система уравнений (12) имеет единственное решение (t, k), то прямые пересекаются в одной точке;

2) если система уравнений (12) не имеет решений, то прямые скрещиваются и тогда выполняется неравенство (11) или, в противном случае, прямые параллельны;

3) если система уравнений (12) имеет более одного решения, то прямые совпадают.

Доказательство очевидно.

Задача 4. Найти точку пересечения двух прямых

и .

Решение. Запишем уравнения обеих прямых в параметрической форме и рассмотрим систему (12).

Если прямые пересекаются, то система (12) должна иметь единственное решение (k, t). Подставляя найденное значение t в параметрические уравнения прямой (или k в параметрические уравнения прямой ), получаем координаты искомой точки.