Головизин_Лекции / Лекция 12. Общее уравнение прямой и плоскости

Лекции по алгебре и геометрии. Семестр 1.

Лекция 12. Общее и нормированное уравнение плоскости и прямой на плоскости.

Краткое содержание: векторное уравнение плоскости и прямой на плоскости, общее уравнение плоскости и прямой на плоскости, неполные уравнения прямой на плоскости и неполные уравнения плоскости, нормированные уравнения прямой на плоскости и плоскости.

Глава 12. Общее и нормированное уравнение плоскости и прямой на плоскости.

п.1. Векторное уравнение плоскости и прямой на плоскости.

Определение. Любой ненулевой вектор, перпендикулярный плоскости (прямой на плоскости) называется нормальным вектором этой плоскости (прямой на плоскости).

Теорема. Пусть – радиус-вектор текущей точки М плоскости (прямой на плоскости), – радиус- вектор какой-нибудь фиксированной точки плоскости (прямой на плоскости), – нормальный вектор плоскости (прямой на плоскости). Тогда уравнение

(1)

является векторным уравнением плоскости (прямой на плоскости).

Доказательство. Изобразим на рисунке прямую L, ее нормальный вектор и радиус-векторы и .

рис.1.

По правилу треугольника сложения векторов имеем:

и точка , откуда и следует доказываемое уравнение (1).

Доказательство для случая плоскости точно такое же, см. рис.2:

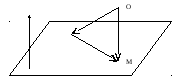
рис.2.

Теорема доказана.

п.2. Общее уравнение плоскости и прямой на плоскости.

Теорема. Для любой прямой на координатной плоскости Оху ее уравнение имеет вид

, (2)

где , – нормальный вектор прямой. Обратно, для любых , где А и В одновременно не равны нулю, уравнение (2) является уравнением прямой, лежащей на координатной плоскости Оху.

Доказательство. 1) Пусть L произвольная прямая на координатной плоскости Оху и пусть точка ее произвольная фиксированная точка, М(х, у) – ее текущая точка, – ее произвольный нормальный вектор. Тогда уравнение (1) является векторным уравнением этой прямой, где , .

Расписывая скалярное произведение в координатной форме, получаем . Раскрывая скобки и группируя, получаем

.

Обозначая через , получаем отсюда равенство (2), которое и будет уравнением данной прямой.

2) Пусть дано уравнение

, (2)

где А, В и С – произвольные действительные числа и пара (А, В) – не нулевая. Пусть для определенности . Тогда , откуда мы видим, что любая пара , где является решением уравнения (2) и, следовательно, это уравнение имеет бесконечное множество решений.

Пусть и – два различных произвольных фиксированных решений уравнения (2), и (х, у) произвольное его решение т.е.

, , .

Отсюда

(3)

и подставляя в оставшиеся два равенства, получаем:

и . (4)

На координатной плоскости Оху каждому решению уравнения (2) соответствует точка. Пусть,

, М(х, у) – точки, соответствующие выбранным решениям. Тогда равенства (4) в векторной форме имеют вид

, , (5)

т.е. и , откуда следует, что

, (6)

что, в свою очередь, означает, что для любой точки М, координаты которой удовлетворяют уравнению (2), точки М, и лежат на одной прямой L, проходящей через фиксированные точки и .

С другой стороны, если точка М(х, у) лежит на этой прямой L, то верно (6), (5) и (4). Подставляя (3) во второе из равенств (4), получаем (2).

Таким образом, уравнению (2) удовлетворяют координаты тех и только тех точек, которые лежат на прямой, ч.т.д.

Теорема доказана.

Определение. Уравнение прямой вида

называется уравнением прямой, проходящей через заданную точку и с заданным нормальным вектором .

Теорема. Уравнение любой плоскости в координатном пространстве Охуz имеет вид

, (7)

где , – нормальный вектор плоскости. Обратно, пусть – произвольные действительные числа, причем числа А, В и С одновременно не равны нулю. Тогда уравнение (7)

является уравнением плоскости в координатном пространстве Охуz.

Доказательство аналогично доказательству предыдущей теоремы, хотя и технически немножко сложнее. Первая часть доказательства практически такая же, а во второй части нужно брать три фиксированных решения (соответственно три точки пространства) и одно произвольное уравнения (7) и доказать, что любое решение уравнения (7), отождествленное с точкой пространства, лежит в той же плоскости, которая проходит через выбранные три точки и, что любая точка пространства лежащая на этой плоскости удовлетворяет уравнению (7).

Определение. Уравнение называется общим уравнением прямой на координатной плоскости Оху. Уравнение называется общим уравнением плоскости. Действительные числа А, В, С, D называются коэффициентами соответствующих уравнений.

п.3. Уравнение прямой в отрезках.

Пусть ни один из коэффициентов А, В, С общего уравнения прямой

,

не равен нулю. Перенесем свободный член С в правую часть уравнения и разделим обе части уравнения на (– С):

.

Обозначим . Тогда последнее уравнение можно записать в виде:

. (8)

Определение. Уравнение вида (8) называется уравнением прямой в отрезках.

Для построения прямой достаточно взять две точки на этой прямой. Для построения прямой в отрезках удобно найти ее точки пересечения с координатными осями:

М(а, 0) – точка пересечения прямой (8) с осью Ох и

N(0, b) – точка пересечения прямой (8) с осью Оу.

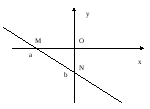
рис.3.

Говорят, что прямая отсекает от координатных осей отрезки ОМ и ОN величина которых равна числам а и b соответственно.

Замечание. Под величиной отрезка ОА здесь понимается не его длина , а координата точки М, т.е. число а. Аналогично, величина отрезка ОN равна числу b.

Пример. Построить прямую .

Решение. Запишем данное уравнение прямой в виде уравнения прямой в отрезках. Для этого перенесем коэффициент – 6 в правую часть уравнения:

и разделим обе части уравнения на 6:

. После сокращения получаем:

.

Данная прямая отсекает от оси Ох отрезок величина которого равна 3, а от оси Оу – отрезок, величина которого равна –2.

Откладываем на оси Ох точку с координатой 3, а на оси Оу откладываем точку с координатой –2 и проводим через эти точки прямую:

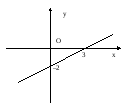
рис.4.

п.4. Неполные уравнения прямой на плоскости.

Определение. Уравнение

(2)

называется неполным уравнением прямой на плоскости, если хотя бы один из его коэффициентов А, В, С равен нулю.

Если коэффициент , , то из уравнения (2) следует . Это уравнение прямой, параллельной оси Оу, отсекающей от оси Ох отрезок величиной а.

Если коэффициент , то из уравнения (2) следует . Это уравнение прямой, параллельной оси Ох, отсекающей от оси Оу отрезок величиной b.

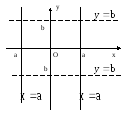
рис.5.

Если , то уравнение (2) принимает вид

. (9)

Ясно, что эта прямая проходит через начало координат.

Если в уравнении (9) коэффициент , то отсюда получаем . Обозначив через , получаем уравнение, которое носит название уравнения прямой с угловым коэффициентом , которое изучалось в школьном курсе алгебры.

Если в уравнении (9) , то и, сокращая на А, получаем уравнение оси Оу: .

Если в уравнении (9) , то и, сокращая на В, получаем уравнение оси Ох: .

Подведем итог исследования общего уравнения прямой

(2)

1) Если , то уравнение (2) может быть записано в виде уравнения прямой в отрезках:

– прямая, отсекающая от осей координат отрезки величиной а и b соответственно.

2) Если , то уравнение может быть записано в виде:

– прямая параллельная оси Ох и отсекающая от оси Оу отрезок величины b.

3) Если , то уравнение может быть записано в виде:

– прямая параллельная оси Оу и отсекающая от оси Ох отрезок величины а.

4) Если , то уравнение прямой имеет вид

– прямая совпадает с осью Ох.

5) Если , то уравнение прямой имеет вид

– прямая совпадает с осью Оу.

6) Если , то уравнение может быть записано в виде: – уравнение прямой с угловым коэффициентом.

п.5. Уравнение плоскости в отрезках. Неполные уравнения плоскости.

Исследование общего уравнения плоскости

, (7)

где – координаты ее нормального вектора, производится аналогично исследованию общего уравнения прямой на плоскости. Приведем ниже все случаи.

Если , то уравнение (7) может быть записано в виде уравнения плоскости в отрезках:

(10)

– плоскость, отсекающая от осей координат отрезки величиной а, b и с соответственно, где обозначено

.

рис.6.

Определение. Уравнение

называется неполным уравнением плоскости, если хотя бы один из его коэффициентов А, В, С, D равен нулю.

Если , то уравнение (7) имеет вид

. (11)

В координатной плоскости Оуz это уравнение есть уравнение прямой, а так как , то данная плоскость параллельна оси Ох. Уравнение (11) может быть записано в виде

(12)

или – уравнение плоскости параллельной координатной плоскости Охz и отсекающей от оси Оу отрезок величины b,

или – уравнение плоскости параллельной координатной плоскости Оху и отсекающей от оси Оz отрезок величины с.

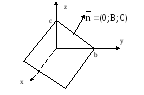
рис.7.

рис.8.

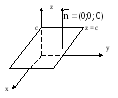
рис.9.

Если , то уравнение (6) имеет вид

. (13)

Это уравнение прямой в координатной плоскости Оуz, проходящая через начало координат и в то же время уравнение плоскости, содержащей ось Ох.

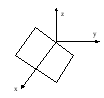
рис.10.

Если в уравнении (13) , то получаем

– уравнение координатной плоскости Оху.

Если в уравнении (13) , то получаем

– уравнение координатной плоскости Охz.

Ситуации, когда или исследуются аналогично.

Подведем итог исследованию общего уравнения плоскости

. (7)

1) Если , то можно уравнение (7) записать в виде уравнения в отрезках

,

где а, b, с – величины отсекаемых плоскостью от координатных осей отрезков.

2) Если , но один из коэффициентов А, В, С равен нулю, то получаем уравнение плоскости в виде

или или

– плоскость параллельная оси Оz или Оу или Ох соответственно.

3) Если , но два из коэффициентов А, В, С равны нулю, то получаем уравнение плоскости в виде

или или

– соответственно плоскость параллельна координатной плоскости Оуz или Охz или Оху.

4) Если , то уравнение (7) принимает вид

– плоскость содержит начало координат.

5) Если и один из коэффициентов А, В, С равен нулю, то получаем уравнение плоскости в виде

или или

– плоскость содержит соответственно ось Ох или ось Оу или ось Оz.

6) Если и два из коэффициентов А, В, С равны нулю, то получаем уравнение плоскости в виде или или – уравнение соответственно координатных плоскостей Оуz или Охz или Оху.

п.6. Нормированное уравнение плоскости и прямой на плоскости.

Пусть

(1)

– векторное уравнение плоскости или прямой на плоскости, где – нормальный вектор плоскости (прямой), – радиус-вектор фиксированной точки плоскости (прямой), – радиус-вектор текущей точки плоскости (прямой).

Заметим, что в уравнении (1) длина нормального вектора не играет никакой роли. Выберем в уравнении (1) в качестве нормального вектора нормальный вектор единичной длины , а направление нормального вектора выберем такое, чтобы угол между вектором и был острый. Смотри следующие рисунки.

рис.11.

рис.12.

Иначе, направление вектора должно быть от начала координат к плоскости (прямой). Раскроем в уравнении (1) скобки

и разделим обе части уравнения на , если скалярное произведение или на , если . Получим

, (14)

где .

Обозначим и пусть , . Так как координатами единичного вектора являются его направляющие косинусы, то . Подставляя в (14), получаем

.

Определение. Уравнение вида

, (15)

где , – направляющие косинусы нормального вектора плоскости, называется нормированным (нормальным) уравнением плоскости.

В случае прямой на координатной плоскости Оху имеем: , , и

.

Определение. Уравнение вида

, (16)

где , – направляющие косинусы нормального вектора прямой, называется нормированным (нормальным) уравнением прямой на координатной плоскости Оху.

Заметим, что в уравнениях (15) и (16) свободный коэффициент (– р) отрицательный, р численно равно расстоянию от начала координат до плоскости (прямой):

.

В этом заключается геометрический смысл свободного члена р в этих уравнениях.

Пример. Записать нормированное уравнение плоскости, если его общее уравнение имеет вид:

и найти расстояние от начала координат до плоскости.

Решение. Имеем, , .

Так как свободный коэффициент этого уравнения равен положительному числу 26, то для получения нормированного уравнения плоскости разделим обе части общего уравнения на число, противоположное модулю нормального вектора:

.

Ответ: – нормированное уравнение плоскости. Расстояние от начала координат до плоскости равно 2.

Аналогично приводится к нормальному виду общее уравнение прямой.