Головизин_Лекции / Лекция 14. Уравнения пучка и связки плоскостей

Лекции по алгебре и геометрии. Семестр 1.

Лекция 14. Уравнения пучка прямых на плоскости, пучка плоскостей и связки плоскостей.

Краткое содержание: пучок прямых на координатной плоскости и его уравнение, уравнение прямой, проходящей через заданную точку, пучок плоскостей и его уравнение, связка плоскостей и его уравнение, основные типы задач на прямые и плоскости.

Глава 14. Уравнения пучка прямых на плоскости, пучка плоскостей и связки плоскостей.

п.1. Уравнение пучка прямых на плоскости.

Определение. Пучком прямых на плоскости называется множество всех прямых данной плоскости, имеющих одну общую точку, которая называется центром пучка.

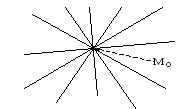
рис.1.

На рис.1 точка – центр пучка.

Теорема. Пусть

и

– две прямые в координатной плоскости Оху, пересекающиеся в точке . Тогда уравнение

, (1)

где – произвольные действительные числа одновременно не равные нулю, есть уравнение пучка прямых с центром пучка в точке .

Доказательство.

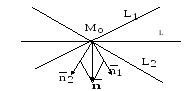
рис.2.

Пусть L – призвольная прямая этого пучка с центром пучка в точке и – ее нормальный вектор. Тогда векторное уравнение прямой L имеет вид:

, (2)

где – радиус-вектор точки , – текущий радиус-вектор, т.е. радиус-вектор текущей точки .

Так как прямые и по условию теоремы пересекаются, то их нормальные векторы не коллинеарные и, следовательно, образуют базис.

Тогда вектор может быть разложен по этому базису:

,

где – кэффициенты этого разложения одновременно не равные нулю, т.к. по определению нормальный вектор . Подставляя в (2) получаем или

. (3)

Но и – векторные уравнения прямых и , т.е. ,

.

Подставляя в (3), получаем равенство (1).

Таким образом, мы доказали, что уравнение любой прямой из данного пучка имеет вид (1).

Обратно, докажем, что при любых , одновременно не равных нулю, уравнение (1) есть уравнение некоторой прямой из данного пучка.

Действительно, с одной стороны, при любых , одновременно не равных нулю, уравнение (1) есть общее уравнение прямой

.

С другой стороны, пусть в уравнении (1) – произвольные действительные числа, одновременно не равные нулю, и пусть – координаты центра пучка. Так как и , то координаты центра пучка удовлетворяют уравнениям прямых и :

и .

Тогда, подставляя координаты точки в уравнение (1), получаем

, т.е. уравнение (1) есть уравнение прямой, проходящей через точку , а значит прямая принадлежит данному пучку, ч.т.д.

Теорема доказана.

Замечание. Если в (1) , то уравнение (1) есть уравнение прямой . Если , то уравнение (1) есть уравнение прямой . Поэтому, если уравнение (1) рахделить на , то получим уравнение любой прямой из данного пучка, кроме прямой :

. (4)

Пример. Написать уравнение произвольной прямой, проходящей через заданную точку .

Решение. Искомая прямая есть прямая пучка прямых с центром пучка в точке . Очевидно, следующие две прямые принадлежат этому пучку:

и

Или , . Тогда уравнение любой прямой этого пучка имеет вид

.

Если заменить в этом уравнении греческие буквы на латинские, получаем

(5)

– уравнение прямой, проходящей через заданную точку . В частности, при , получаем уравнение пучка прямых с центром пучка в начале координат: .

Разделив уравнение (5) на , получаем уравнение прямой с угловым коэффициентом, проходящей через заданную точку :

, (6)

а при , получаем уравнение прямой с угловым коэффициентом, проходящей через начало координат:

.

Другими словами, уравнение , где , есть уравнение пучка прямых с центром пучка в начале координат.

п.2. Уравнение связки плоскостей.

Определение. Связкой плоскостей называется множество всех плоскостей, имеющих одну общую точку, которая называется центром связки.

Теорема. Пусть , ,

– три плоскости в ПДСК Охуz, имеющие единственную общую точку . Тогда уравнение , (7)

где – произвольные действительные числа одновременно не равные нулю, есть уравнение связки плоскостей с центром связки в точке .

Доказательство практически один к одному повторяет доказательство предыдущей теоремы об уравнении пучка прямых.

Пример. Найти уравнение связки плоскостей с центром связки в точке .

Решение. Очевидно, что следующие три плоскости пересекаются в единственной точке :

, , .

Тогда уравнение

, (8)

где и одновременно не равны нулю, есть искомое уравнение.

В частности, если , то уравнение

(9)

есть уравнение связки плоскостей с центром связки в начале координат.

п.3. Уравнение пучка плоскостей.

Определение. Пучком плоскостей называется множество всех плоскостей пересекающихся по одной и той же прямой, называемой осью пучка.

рис.3.

Теорема. Пусть

и

– две плоскости, пересекающиеся по прямой L. Тогда уравнение

, (10)

где – произвольные действительные числа одновременно не равные нулю, есть уравнение пучка плоскостей с осью пучка L.

Доказательство аналогично доказательству теоремы об уравнении пучка прямых и предоставляется читателю.

Пример. Найти уравнение пучка плоскостей, осью которого является ось абсцисс.

Решение. Очевидно, что координатные плоскости

и пересекаются по оси Ох.

рис.4.

Тогда уравнение (10) в данном случае принимает вид

. Заменив греческие буквы на латинские, получаем

, (11)

где – произвольные действительные числа, одновременно не равные нулю. Уравнение (11) есть искомое уравнение пучка плоскостей с осью пучка Ох.

Аналогично, уравнение

, (12)

есть уравнение пучка плоскостей с осью пучка Оу, а уравнение

(13)

есть уравнение пучка плоскостей с осью пучка Оz.

п.4. Основные задачи на прямые и плоскости.

Задача 1. Найти уравнение прямой, проходящей через две заданные точки и .

Эта задача нами уже решена, см. лекцию 11, параграф 4, задача 1:

.

Задача 2. Найти угол между двумя прямыми

и .

Эта задача была решена в лекции 11, параграф 4:

Искомый угол равен либо углу между их направляющими векторами

,

или .

Задача 3. Найти общее уравнение плоскости, если известны координаты ее нормального вектора и координаты точки , лежащей на данной плоскости.

Решение. Одно решение этой задачи приведено в параграфе 2, формула (8).

, (8)

Это же уравнение можно получить и по другому. Общее уравнение плоскости имеет вид

,

где – координаты ее нормального вектора. Осталось найти коэффициент D. С этой целью подставим в уравнение координаты точки : , откуда .

Подставляя в уравнение получаем:

или

– искомое уравнение плоскости.

Задача 4. Найти уравнение плоскости, проходящей через три заданные точки , и .

Решение.

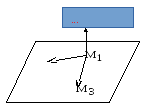
рис.11.

Как мы видели в задаче 3, для составления общего уравнения плоскости достаточно знать координаты ее нормального вектора и координаты любой точки, лежащей на данной плоскости.

В качестве нормального вектора плоскости можно взять векторное произведение вектора на вектор , а в качестве точки, лежащей на плоскости можно взять точку . Получаем

,

где .

Искомое уравнение плоскости можно получить и в другом виде. Уравнение плоскости в векторной форме имеет вид

,

откуда

или

.

Задача 5. Найти угол между двумя плоскостями.

Решение. Из геометрии нам известно, что двугранный угол между двумя плоскостями измеряется линейным углом (см. рис.12).

рис.12.

Нетрудно видеть, что линейный угол , измеряющий двугранный угол между двумя плоскостями равен углу между нормальными векторами этих плоскостей или равен . Здесь используется признак равенства углов со взаимно перпендикулярными сторонами.

Итак,

или .

Таким образом, задача вычисления угла между плоскостями сводится к задаче вычисления угла между векторами.

Задача 6. Найти расстояние от заданной точки до заданной плоскости

.

Решение. Выберем произвольную точку , лежащую на данной плоскости. Заметим, что если , то начало координат лежит на плоскости и его можно взять в качестве точки . Если же , то в качестве такой точки можно взять точку пересечения плоскости с одной из координатных осей. Так как плоскость не может быть параллельной всем трем координатным осям, то хотя бы одна координатная ось пересекает данную плоскость.

Пусть, например, – точка пересечения плоскости с координатной осью Ох. Здесь , если .

рис.13.

Итак, пусть точка тем или иным способом выбрана, тогда расстояние от заданной точки до заданной плоскости равно модулю проекции вектора на нормальный вектор плоскости :

.

Так как , то эту формулу можно записать в виде

. (14)

Определение. Пусть дано произвольное общее уравнение плоскости и произвольная точка пространства . Число

называется невязкой точки относительно плоскости .

С помощью введенного понятия невязки, формула расстояния от точки до плоскости иожет быть записана в виде:

.

Определение. Величина

(15)

называется отклонением точки от плоскости .

Из последнего определения следует, что расстояние от точки до плоскости равно модулю отклонения точки от плоскости :

. (16)

Из формулы (21) видно, что отклонение и невязка имеют одинаковый знак.

Замечание. Формулы (14) – (16) можно записать в другом виде. Приведем данное уравнение плоскости к нормальному виду:

,

где ,

, причем знак плюс берется в случае, когда и минус, в противном случае.

Теперь, формула (14) расстояния от точки до плоскости принимает вид:

, (17)

где

(18)

– отклонение точки от плоскости .

Задача 7. Найти расстояние от данной точки до данной прямой .

Решение. Задача решается аналогично предыдущей.

рис.14.

. Так как , то

.

Аналогично вводятся понятия невязки точки относительно прямой и отклонения точки от прямой.

Определение. Пусть дано произвольное общее уравнение прямой и произвольная точка плоскости . Число

называется невязкой точки относительно прямой L.

Определение. Величина

называется отклонением точки от плоскости .

Если привести уравнение прямой к нормальному виду:

,

где

,

, причем знак плюс берется в случае, когда и минус, в противном случае, то формула расстояния от точки до прямой принимает вид:

,

где

– отклонение точки от прямой L.

Задача 8. Найти расстояние между двумя параллельными плоскостями.

Решение. 1-й способ. Найти на одной плоскости произвольную точку и найти расстояние от нее до второй плоскости, т.е. свести эту задачу к задаче 6.

2-й способ. Приведем оба уравнения параллельных плоскостей к нормальному виду:

,

где и – нормальные векторы плоскостей и соответственно, , – расстояния от начала координат до плоскостей и соответственно.

Так как нормальные векторы и направлены от начала координат к плоскости, то возможны 2 случая:

а) . На следующем рисунке схематически изображены две параллельнве плоскости и и их единичные нормальные векторы, отложенные от начала координат О.

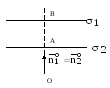
рис.15.

Здесь, , – расстояния от начала координат до соответствующих плоскостей. Так как неизвестно, какая плоскость ближе к началу координат, то расстояние между плоскостями

.

б) . Так как нормальные векторы и направлены от начала координат к плоскостям и противоположны,то начало координат находится между плоскостями, см. следующий рисунок.

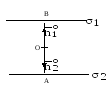
рис.16.

Здесь, как и в предыдущем случае, , – расстояния от начала координат до соответствующих плоскостей. Отсюда следует, что расстояние между плоскостями

.

Задача 9. Найти расстояние между двумя параллельными прямыми.