Головизин_Лекции / Лекция 13. Взаимное расположение прямых и плоскостей

Лекции по алгебре и геометрии. Семестр 1.

Лекция 13. Взаимное расположение плоскостей и прямых.

Краткое содержание: уравнение прямой на плоскости с угловым коэффициентом, взаимное расположение двух прямых на плоскости, двух плоскостей в пространстве, плоскости и прямой в пространстве, трех плоскостей в пространстве

Глава 13. Взаимное расположение плоскостей и прямых.

п.1. Уравнение прямой с угловым коэффициентом.

Пусть дана прямая L на координатной плоскости Оху.

Определение. Углом наклона прямой к оси абсцисс называется угол поворота оси абсцисс вокруг любой ее точки против часовой стрелки до положения параллельности (или совпадения) с данной прямой.

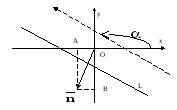
рис.1.

Из определения следует, что угол наклона прямой L к оси Ох может изменяться от нуля до : . Если прямая , то .

Пусть

(1)

– общее уравнение прямой L, где – нормальный вектор прямой L и . Тогда и (см. рис.1). Выразим у из уравнения (1)

.

Обозначим

, .

Уравнение прямой L принимает вид:

.

Определение. Уравнение прямой вида

(2)

называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой.

Теорема. В уравнении прямой с угловым коэффициентом

угловой коэффициент k равен тангенсу угла наклона прямой к оси абсцисс:

. (3)

Доказательство. 1) Если прямая , то и . С другой стороны, ее нормальный вектор и .

Тогда и, следовательно, , ч.т.д.

2) Пусть , тогда , и . Пусть F – точка пересечения прямой L с осью абсцисс. Тогда

, .

Опишем окружность единичного радиуса с центром в точке F , а в точке оси Ох с координатой проведем касательную m к этой окружности. См. рис.2.

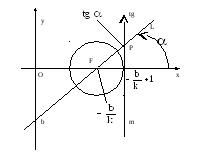
рис.2.

Выберем положительное направление на прямой m, так, чтобы . Тогда ось m является осью тангенсов для данной единичной (тригонометрической) окружности.

Пусть Р – точка пересечения прямой L с осью тангенсов m. Тогда, с одной стороны, , где – угол наклона прямой L к оси Ох, а, с другой стороны, точка и , откуда и следует равенство , ч.т.д.

Теорема доказана.

Заметим, что приведенное доказательство принадлежит автору этих лекций. Достоинством этого доказательства является то, что оно не зависит ни от величины угла наклона , ни от величины коэффициента .

В заключение отметим, что коэффициент b в уравнении (2) равен величине отрезка, отсекаемого прямой от оси ординат (см. рис.2).

п.2. Взаимное расположение двух прямых на плоскости.

Этот вопрос уже обсуждался в предыдущей лекции, когда оба уравнения данных прямых записывались в каноническом или параметрическом виде. Пусть сейчас оба уравнения прямых записаны в общем виде.

Теорема. Пусть

и

– общие уравнения двух прямых на координатной плоскости Оху. Тогда

1) если , то прямые и совпадают;

2) если , то прямые и

параллельные;

3) если , то прямые пересекаются.

Доказательство. Условие равносильно коллинеарности нормальных векторов данных прямых:

. Поэтому, если , то и прямые пересекаются.

Если же , то , , и уравнение прямой принимает вид:

или , т.е. прямые совпадают. Заметим, что коэффициент пропорциональности , иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.

Если же прямые не совпадают и не пересекаются, то остается случай , т.е. прямые параллельны.

Теорема доказана.

Заметим, что если прямые пересекаются, то для нахождения координат их точки пересечения достаточно решить систему двух уравнений с двумя неизвестными:

. (4)

Следствие. Пусть – определитель системы (4). Если , то прямые пересекаются в одной точке и система (4) имеет единственное решение, которое можно найти по формулам Крамера:

, (5)

где , .

Если , то прямые или параллельны и тогда система (4) не имеет решений, или прямые совпадают и тогда система (4) имеет бесконечно много решений.

Доказательство. По определению определителя второго порядка

.

Если , то и , т.е. прямые пересекаются и координаты точки пересечения можно найти по формулам Крамера (5).

Если же , то и , т.е. либо прямые параллельны и тогда система не может иметь ни одного решения, либо прямые совпадают и тогда система (4) состоит из одного уравнения и решениями такой системы являются координаты любой точки, лежащей на прямой, а их бесконечно много.

следствие доказано.

Пример. Выяснить взаимное расположение двух прямых

и

и если они пересекаются, найти их точку пересечения.

Решение. Решим систему

.

Определитель системы

,

следовательно прямые пересекаются. Вычисляем координаты точки пересечения:

, ,

, .

Ответ. Прямые пересекаются в точке .

п.3. Взаимное расположение двух плоскостей.

Плоскости могут совпадать, быть параллельными или пересекаться по прямой.

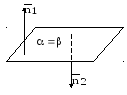
рис.3.

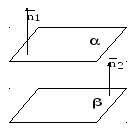
рис.4.

рис.5.

Теорема. Пусть

и

– общие уравнения двух плоскостей. Тогда:

1) если , то плоскости совпадают;

2) если , то плоскости параллельны;

3) если или , то плоскости пересекаются и система уравнений

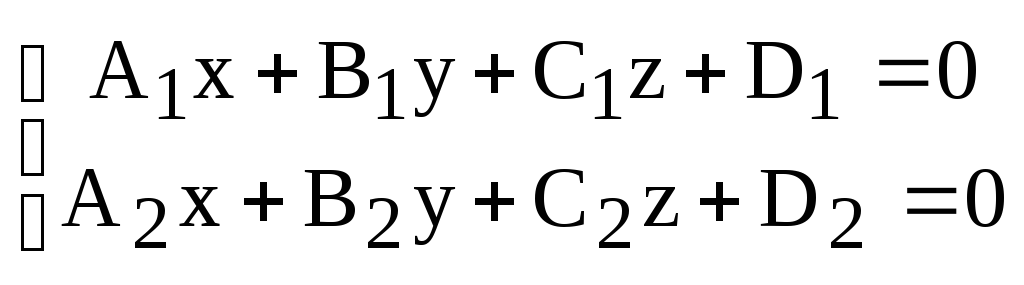(6)

является уравнениями прямой пересечения данных плоскостей.

Доказательство. Первое и второе условия теоремы равносильны коллинеарности нормальных векторов данных плоскостей:

.

Если , то , , , и уравнение плоскости принимает вид:

Коэффициент пропорциональности k не может быть равен нулю, т.к. и при получаем, что , что противоречит определению нормального вектора. Следовательно, уравнение плоскости

совпадает с уравнением плоскости , а это означает, что плоскости совпадают.

Если , то это означает коллинеарность нормальных векторов обеих плоскостей, а значит плоскости либо параллельны, либо совпадают. Но в этом случае плоскости не могут совпадать и остается единственная возможность их параллельности.

Третье условие теоремы равносильно тому, что нормальные векторы плоскостей не коллинеарные, а потому они не совпадают и не параллельны, а следовательно, они пересекаются. Из геометрии известно, что линия пересечения двух плоскостей является прямой.

Точка М лежит на прямой пересечения двух плоскостей и тогда и только тогда, когда она лежит одновременно на обеих плоскостях и ее координаты удовлетворяют обоим уравнениям системы (6), т.е. являются решением этой системы. А это означает, что система (6) является уравнениями прямой пересечения плоскостей, ч.т.д.

Теорема доказана.

п.4. Взаимное расположение прямой и плоскости в пространстве.

Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.

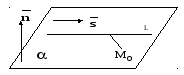
рис.6.

рис.7.

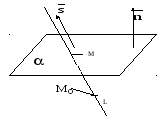
рис.8.

Теорема. Пусть плоскость задана общим уравнением

,

а прямая L задана каноническими уравнениями

или параметрическими уравнениями

, ,

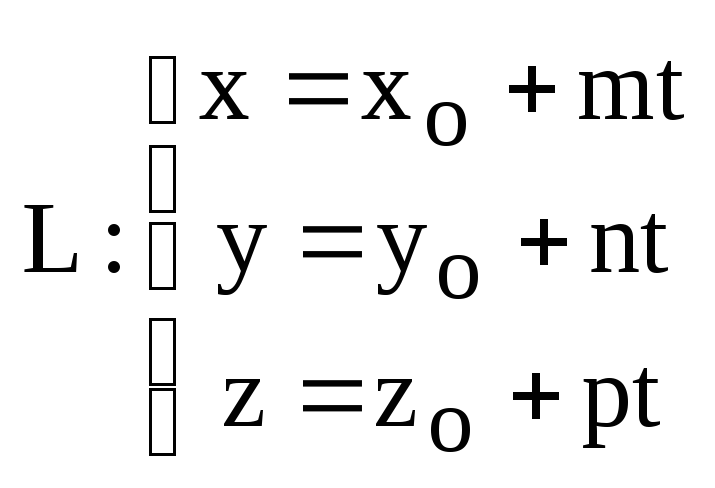в которых – координаты нормального вектора плоскости , – координаты произвольной фиксированной точки прямой L, –

координаты направляющего вектора прямой L. Тогда:

1) если , то прямая L пересекает плоскость в точке, координаты которой можно найти из системы уравнений

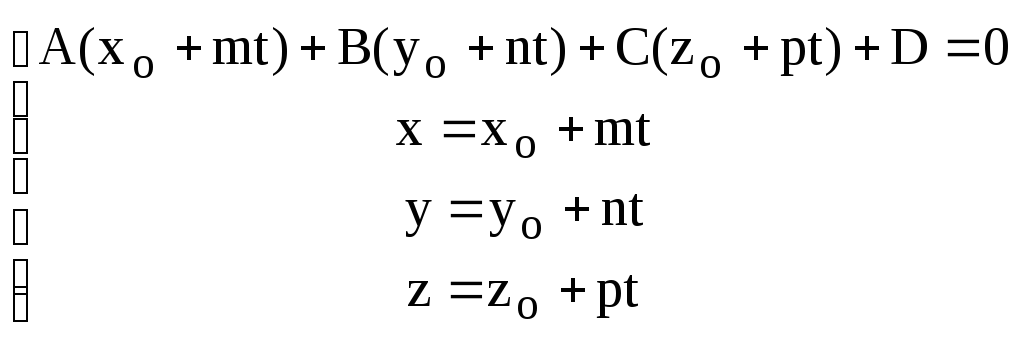; (7)

2) если и , то прямая лежит на плоскости;

3) если и , то прямая параллельна плоскости.

Доказательство. Условие говорит о том, что вектроры и не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.

Если , то это означает, что . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка . Если , то точка – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.

Если , а , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.

Теорема доказана.

п.5. Взаимное расположение трех плоскостей.

Пусть даны три плоскости: , и , , , – их нормальные векторы, соответственно. Рассмотрим все возможные случаи.

1) Все три плоскости совпадают: . Очевидно, что в этом случае .

2) Две плоскости совпадают, а третья параллельна им, например: и в этом случае .

3) две плоскости совпадают, а третья пересекает их, например: – прямая пересечения.

В этом случае,

рис.9.

4) Все три плоскости параллельны друг другу: . Тогда .

5) Две плоскости параллельны, а третья пересекает их, например: . В этом случае – прямая пересечения плоскостей и , – прямая пересечения плоскостей и и, как известно из курса геометрии, . Нормальные векторы .

рис.10.

6) Все три плоскости пересекаются по одной прямой и тогда , но все три вектора , и лежат в одной плоскости.

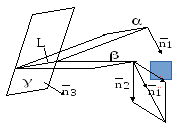
рис.11.

7) Каждая пара плоскостей пересекается по своей прямой, образуя треугольную "трубу" и , но все три вектора , и лежат в одной плоскости.

рис.12.

8) все три плоскости пересекаются в одной точке и их нормальные векторы некомпланарны.

рис.13.

Анализируя все эти случаи, мы приходим к следующему выводу.

Теорема. Пусть даны общие уравнения трех плоскостей:

,

,

,

где , , – их соответствующие нормальные векторы. Тогда:

1) если смешанное произведение

,

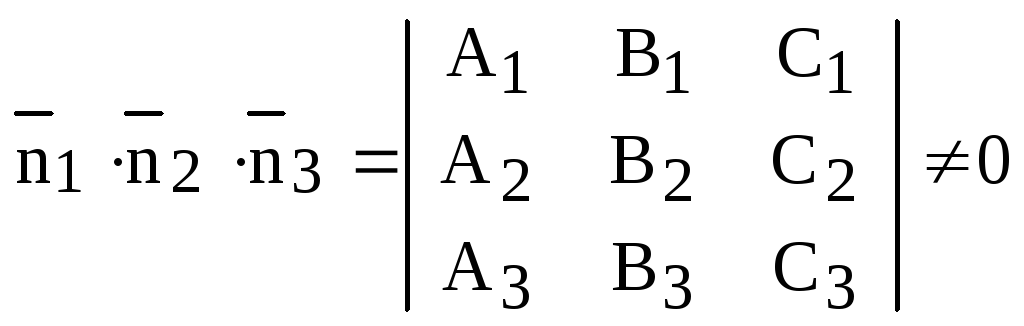то все три плоскости пересекаются в одной точке, координаты которой можно найти решив систему уравнений

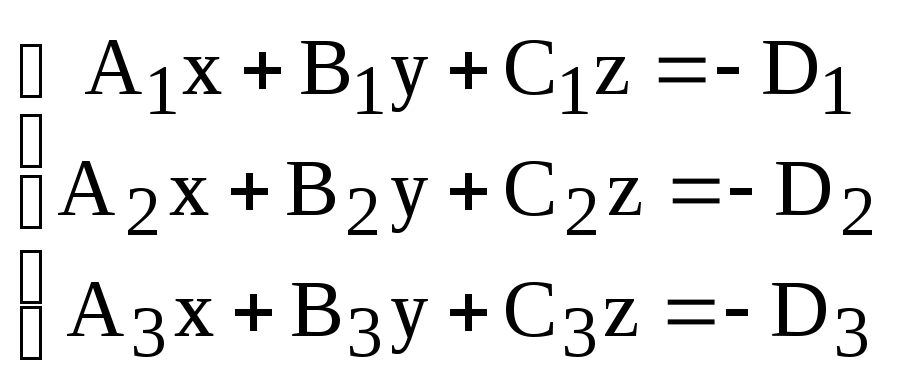, (8)

используя, например, формулы Крамера:

, , ,

где – определитель системы,

, , ;

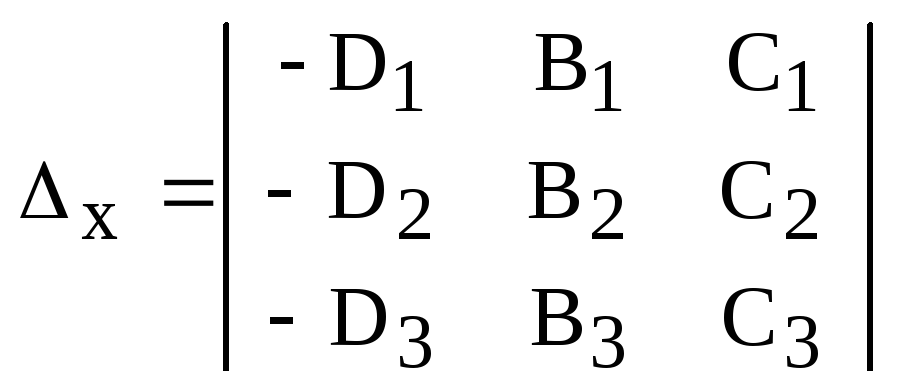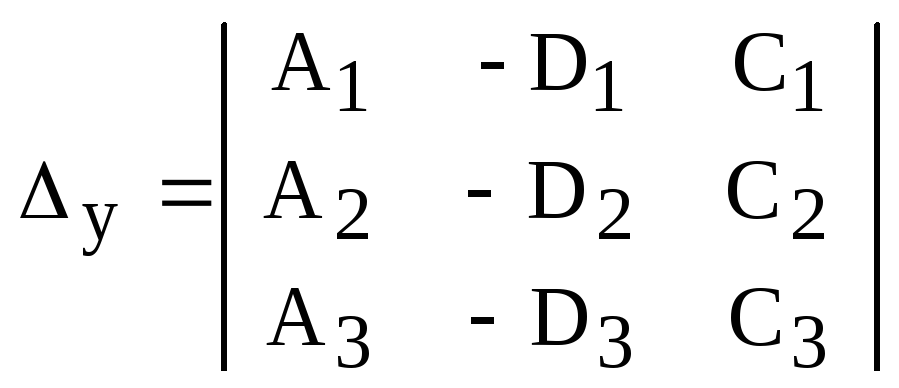2) если смешанное произведение

,

а система уравнений (8) не имеет решений, то имеет место случай 2, 4, 5 или 7 из рассмотренных выше.

3) если смешанное произведение

,

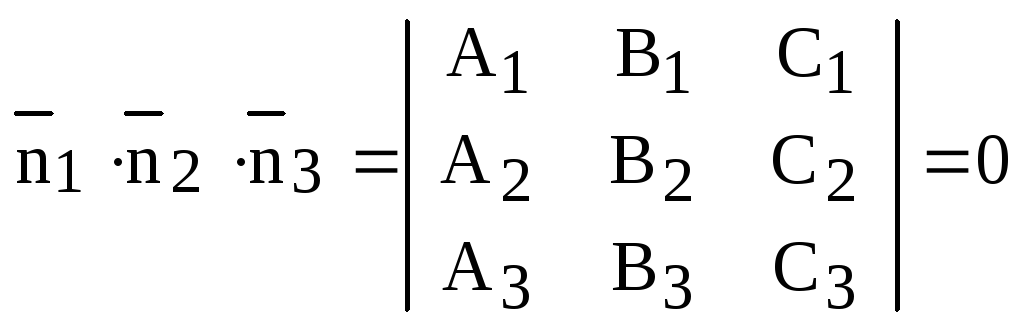а система уравнений (8) имеет бесконечно много решений, то имеет место случай 1, 3, или 6 из рассмотренных выше.

Доказательство очевидно.

Замечание 1. Чтобы различать случаи расположения трех плоскостей, если смешанное произведение их нормальных векторов равно нулю, необходимо исследовать эти плоскости попарно, выявлять, нет ли среди них совпадающих или параллельных. Если совпадающих или параллельных плоскостей нет, то имеет место либо случай 6, либо случай 7 из рассмотренных выше. Но в случае 6, система (8) имеет решения, а в случае 7 – нет.

Замечание 2. Если среди трех плоскостей есть хотя бы одна пара пересекающихся плоскостей, например, – плоскости и пересекаются по прямой L, то исследование взаимного расположения трех плоскостей можно свести к исследованию расположения прямой L и плоскости , правда для этого нужно записать уравнение прямой L не в виде пересечения двух плоскостей:

,

а в каноническом или параметрическом виде.

Задача. Найти канонические уравнения прямой, заданной в виде пересечения двух плоскостей:

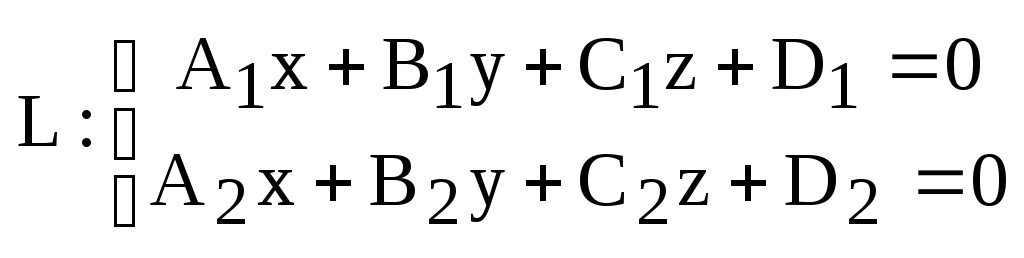. (9)

Решение. Пусть и – нормальные векторы плоскостей в системе (9). Так как прямая перпендикулярная плоскости перпендикулярна любой прямой лежащей в этой плоскости, то оба нормальных вектора перпендикулярны прямой пересечения L и их векторное произведение будет вектором коллинерным этой прямой.

рис.14.

Таким образом, вычисляя векторное произведение нормальных векторов плоскости (неважно в каком порядке), мы находим направляющий вектор прямой L:

.

Для написания канонических уравнений прямой необходимо знать координаты какой-нибудь точки лежащей на прямой L. С этой целью, найдем какое-нибудь решение системы (9). Т.к. любое решение системы (9) есть координаты точки лежащей на прямой L, то тем самым мы находим точку на прямой L.

Теперь осталось написать канонические уравнения прямой L:

.