golovizin_lekcii_po_lineynoy_algebre_2_semestr / Лекция 24. Матрица перехода

Головизин В.В. Лекции по алгебре и геометрии. Лекция 24. 6

Лекции по алгебре и геометрии. Семестр 2.

Лекция 24. Матрица перехода и ее свойства.

Краткое содержание: конечномерное векторное пространство и существование его базиса, дополнение до базиса, разложение вектора по базису, координаты вектора относительно базиса, действия с векторами в координатной форме, изоморфизм векторного пространства и пространства столбцов, матрица перехода от одного базиса к другому, изменение координат вектора при изменении базиса, свойства матрицы перехода.

п.1. Существование базиса векторного пространства.

Определение. Векторное пространство называется конечномерным, если оно обладает конечной порождающей системой векторов.

Замечание. Мы будем изучать только конечномерные векторные пространства. Несмотря на то, что мы уже довольно много знаем о базисе конечномерного векторного пространства, у нас нет уверенности, что базис такого пространства вообще существует. Все ранее полученные свойства были получены в предположении, что базис существует. Следующая теорема закрывает этот вопрос.

Теорема. (О существовании базиса конечномерного векторного пространства.)

Любое конечномерное векторное пространство обладает базисом.

Доказательство. По условию существует конечная порождающая система векторов данного конечномерного векторного пространства V: .

Мы можем считать, что все векторы этой системы ненулевые, ибо в противном случае, мы можем удалить их из этой системы и оставшаяся система векторов будет конечной порождающей системой.

Заметим сразу же, что если порождающая система векторов является пустой, т.е. не содержит ни одного вектора, то по определению полагают, что данное векторное пространство является нулевым, т.е. . В этом случае по определению полагают, что базисом нулевого векторного пространства является пустой базис и его размерность по определению полагают равной нулю.

Пусть далее, ненулевое векторное пространство и система ненулевых векторов является его конечной порождающей системой.

Если эта система линейно независимая, то все доказано, т.к. линейно независимая и порождающая система векторов векторного пространства является его базисом.

Если же данная система векторов является линейно зависимой, то один из векторов этой системы линейно выражается через оставшиеся и его можно удалить из системы, причем оставшаяся система векторов, будет по-прежнему порождающей.

Перенумеруем оставшуюся систему векторов: . Далее рассуждения повторяются.

Если эта система линейно независимая, то она является базисом. Если же нет, то снова найдется вектор в этой системе, который можно удалить, а оставшаяся система будет порождающей.

Повторяя этот процесс, мы не можем остаться с пустой системой векторов, т.к. в самом крайнем случае мы придем к порождающей системе из одного ненулевого вектора, которая является линейно независимой, а, следовательно, базисом. Поэтому, на каком-то шаге мы приходим к линейно независимой и порождающей системе векторов, т.е. к базису, ч.т.д.

Теорема доказана.

Лемма. Пусть . Тогда:

1. Любая система из вектора является линейно зависимой.

2. Любая линейно независимая система из векторов является его базисом.

Доказательство. 1). По условию леммы, число векторов в базисе равно и базис является порождающей системой, поэтому число векторов в любой линейно независимой системе не может превосходить , т.е. любая система содержащая вектор является линейно зависимой.

2). Как следует из только что доказанного, любая линейно независимая система из векторов этого векторного пространства является максимальной, а следовательно, базисом.

Лемма доказана.

Теорема (О дополнении до базиса.) Любая линейно независимая система векторов векторного пространства может быть дополнена до базиса этого пространства.

Доказательство. Пусть векторное пространство размерности n и некоторая линейно независимая система его векторов. Тогда .

Если , то по предыдущей лемме, эта система является базисом и доказывать нечего.

Если же , тогда данная система является не максимальной линейной независимой системой (иначе она была бы базисом, что невозможно, т.к. ). Следовательно, найдется вектор , такой, что система – линейно независимая.

Если, теперь , то система является базисом.

Если же , все повторяется. Процесс пополнения системы не может продолжаться бесконечно, т.к. на каждом шаге мы получаем линейно независимую систему векторов пространства , а по предыдущей лемме число векторов в такой системе не может превышать размерности пространства. Следовательно, на каком-то шаге мы придем к базису данного пространства.

Теорема доказана.

Пример. Пусть К - произвольное поле, – арифметическое векторное пространство столбцов высоты . Тогда .

Для доказательства рассмотрим систему столбцов этого пространства:

, , ... , .

Мы уже доказали, что эта система линейно независимая. Докажем, что она является порождающей системой столбцов пространства .

Пусть - произвольный столбец. Тогда очевидно равенство: . Т.е. система - порождающая и, следовательно, является базисом. Отсюда, , ч.т.д.

Определение. Базис

, , ... ,

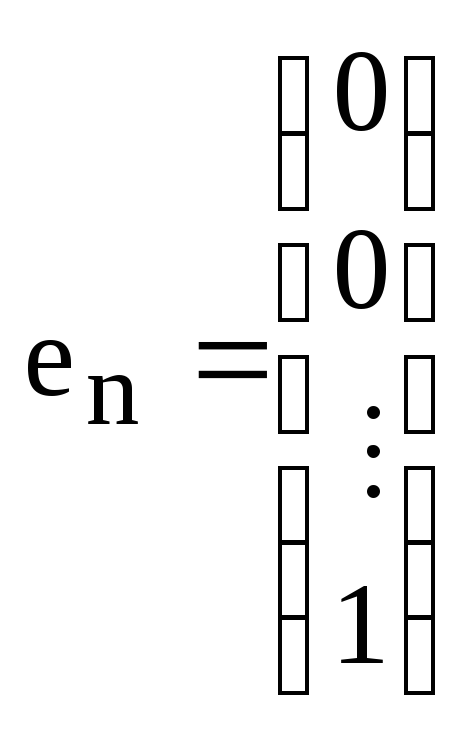
арифметического векторного пространства столбцов высоты n называется каноническим или естественным.

Упражнение.

Докажите, что если порождающая система векторов содержит нулевой вектор, то после его удаления из системы, оставшаяся система векторов будет тоже порождающей.

п.2. Действия с векторами в координатной форме.

Пусть – базис векторного пространства V над полем K и – произвольный вектор векторного пространства V. Из определения базиса следует, что любой вектор можно представить в виде линейной комбинации базисных векторов и притом единственным образом:

. (1)

Определение. Равенство (1) называется разложением вектора х по базису . Коэффициенты линейной комбинации (1): называются координатами вектора х относительно базиса .

Теорема. Пусть – базис векторного пространства V над полем K. Отображение

,

которое каждому вектору ставит в соответствие упорядоченный набор его координат относительно данного базиса является биекцией, т.е. взаимно однозначным соответствием.

Доказательство. Для каждого вектора векторного пространства V существует единственный набор его координат, поэтому соответствие является, по определению, отображением.

Докажем, что отображение является сюръекцией. Пусть – произвольный набор скаляров. Тогда положим, по определению,

.

Так как V – векторное пространство над полем K, то произведение базисных векторов на скаляры поля K являются векторами векторного пространства V:

, .

Сумма векторов векторного пространства V также является его вектором, т.е.

.

Таким образом, для любого упорядоченного набора из n скаляров поля K существует вектор , для которого этот набор скаляров является его координатами относительно данного базиса, т.е.

,

ч.т.д.

Докажем, что отображение является инъекцией.

Пусть, – два произвольных вектора векторного пространства и . Мы хотим доказать, что . Допустим противное, что различным векторам отображение ставит в соответствие один и тот же набор скаляров:

.

Из определения отображения следует, что этот набор скаляров является координатами как вектора х, так и вектора у относительно базиса , т.е.

и , откуда следует, что . Получили противоречие, следовательно, различные векторы имеют различные координаты и , ч.т.д.

Таким образом, отображение является инъекцией и сюръекцией, т.е. биекцией, ч.т.д.

Теорема доказана.

Замечание. В дальнейшем, координаты вектора х будем записывать столбцом и обозначать:

.

В соответствии с обозначениями предыдущей теоремы, будем писать:

.

В этих обозначениях справедлива следующая теорема.

Теорема. Пусть относительно фиксированного базиса векторного пространства V над полем K

, , где – произвольные векторы, и пусть – произвольный скаляр. Тогда справедливы равенства:

1) или

;

2) или

.

Другими словами, при сложении векторов их координаты складываются, а при умножении скаляра на вектор его координаты умножаются на этот скаляр.

Доказательство. Пусть

, .

Складывая вектора х и у, и умножая вектор х на скаляр , получаем:

,

.

Отсюда,

, , ч.т.д.

Теорема доказана.

п.3. Изоморфизм векторных пространств.

Определение. Пусть V и W – произвольные векторные пространства над полем К. Отображение называют гомоморфизмом (или линейным отображением) векторного пространства в векторное пространство , если , :

1) ;

2) .

Определение. Пусть V и W – произвольные векторные пространства над полем К. Гомоморфизм называют изоморфизмом векторного пространства в векторное пространство , если отображение является биекцией (т.е. взаимно однозначным соответствием).

Определение. Если существует изоморфизм , то векторное пространство называют изоморфным векторному пространству .

Обозначение: .

Теорема. На множестве векторных пространств над одним и тем же полем K отношение изоморфизма является отношением эквивалентности, т.е. это отношение обладает свойствами рефлексивности, симметричности и транзитивности:

1) свойство рефлексивности: – любое векторное пространство изоморфно самому себе;

2) свойство симметричности: ;

3) свойство транзитивности: .

Следствие. Если V – векторное пространство над полем K и , то векторное пространство V изоморфно арифметическому векторному пространству столбцов высоты n: .

Доказательство. Отображение , определенное правилом ,

,

где Х – столбец координат вектора х относительно фиксированного базиса векторного пространства V над полем K, является:

1) гомоморфизмом векторных пространств, т.е.

, верны равенства

и ;

2) биекцией.

Отсюда по определению изоморфизма векторных пространств следует, что , ч.т.д.

Отсюда и из следствия легко получить следующий результат.

Теорема. Два конечномерных векторных пространства над одним и тем же полем изоморфны тогда и только тогда, когда равны их размерности.

Отсюда, в частности, следует, что в одном классе эквивалентности оказываются те и только те векторные пространства, которые имеют одинаковую размерность.

Последнее следствие очень важно с практической точки зрения. Какова бы ни была природа векторов векторного пространства: направленные отрезки, многочлены, функции, матрицы или что-либо другое, мы можем заменить изучаемое векторное пространство на изоморфное ему пространство столбцов соответствующей высоты и работать со скалярами, т.е. с числами.

Другими словами, говоря современным языком, мы производим оцифровку векторного пространства, т.е. элемент векторного пространства, вектор х, мы отождествляем с упорядоченным набором чисел, а действия с векторами, их сложение и умножение на скаляр, производим с помощью сложения и умножения чисел, что позволяет нам подключать компьютер при работе с любым конечномерным векторным пространством.

п.4. Матрица перехода.

Пусть , – два базиса произвольного векторного пространства V над полем K. Назовем первый базис "старым", а второй "новым". Разложим векторы нового базиса по старому базису:

(2)

(Обратите внимание на нумерацию коэффициентов!)

Каждое равенство в (2) можно записать в матричной форме, если мы формально воспользуемся правилом умножения строки на столбец. Пусть – строка длины , элементами которой являются векторы старого базиса. Аналогично, – вектор–строка нового базиса. Будем рассматривать эти строки как матрицы соответствующих размеров и производить с ними действия как с числовыми матрицами. (Такие действия можно обосновать.) Тогда, ,

.

Если мы обозначим столбец координат вектора через :

,

то последнее равенство можно записать в виде:

,

а всю систему равенств (2) – в виде:

,

где

.

Таким образом, равенства (2) в матричной форме записи имеют вид:

. (3)

Такая форма записи позволяет значительно облегчить выкладки.

Определение. Матрица

называется матрицей перехода от старого базиса к новому базису .

Матрицу перехода от базиса к базису мы обозначать буквой С или или .

В этих обозначениях равенство (3) принимает вид:

(4)

п.5. Вычисление матрицы перехода в пространстве столбцов.

Для вычисления матрицы перехода применяется равенство (4). Пусть векторы и старого и нового базиса являются столбцами одной высоты, т.е. являются векторами пространства . Тогда столбцы старого и нового базисов образуют матрицы: , . Подставляя их в равенство (4), получаем матричное равенство:

. (5)

Обозначая искомую матрицу перехода буквой Х, получаем матричное уравнение , которое можно

решать методом Гаусса. Решая это матричное уравнение, находим матрицу перехода:

. (6)

Заметим, что столбцы являются базисом пространства столбцов, а потому линейно независимы.

Далее, будет показано (посещайте лекции!), что если столбцы квадратной матрицы линейно независимы, то такая матрица является невырожденной, т.е. ее определитель не равен нулю, а сама матрица обратимая, т.е. имеет обратную.

п.6. Изменение координат вектора при изменении базиса.

Пусть , – два базиса произвольного векторного пространства V и пусть – произвольный вектор. Обозначим через и – столбцы координат вектора х относительно старого и нового базисов соответственно. В таких обозначениях справедлива следующая теорема, которая устанавливает связь между координатами одного и того же вектора в двух различных базисах.

Теорема. .

Доказательство. Все выкладки проведем в матричной форме.

По условию теоремы

или

, (7)

где обозначено

– столбец координат вектора х относительно базиса .

Аналогично,

или

, (8)

где обозначено

– столбец координат вектора х относительно базиса .

Подставляя в равенство (8) равенство (4), получаем:

.

Результатом произведения матрицы на столбец есть столбец, и из полученного равенства следует, что столбец является столбцом координат вектора х относительно базиса . А из равенства (7) следует, что столбец также является столбцом координат вектора х относительно базиса .

Так как любой вектор имеет относительно фиксированного базиса единственный столбец координат, то эти столбцы равны, т.е.

.

Теорема доказана.

п.7. Свойства матрицы перехода.

Лемма. Пусть А и В – две матрицы размера над полем K. Если для любого столбца выполняется равенство , тогда .

Доказательство. Пусть – столбцы матрицы А, – столбцы матрицы В, – канонический базис пространства столбцов .

Подставляем в равенство вместо столбца Х столбцы канонического базиса. Получаем равенство . Легко проверить, что , верны равенства и . Отсюда, , , а значит и , ч.т.д.