golovizin_lekcii_po_lineynoy_algebre_2_semestr / Лекция 22. Векторные пространства

Головизин В.В. Лекции по алгебре и геометрии. 4

Лекции по алгебре и геометрии. Семестр 2.

Лекция 22. Векторные пространства.

Краткое содержание: определение векторного пространства, его простейшие свойства, системы векторов, линейная комбинация системы векторов, тривиальная и нетривиальная линейная комбинация, линейно зависимые и независимые системы векторов, условия линейной зависимости или независимости системы векторов, подсистемы системы векторов, системы столбцов арифметического векторного пространства.

п.1. Определение векторного пространства и его простейшие свойства.

Здесь, для удобства читателя, мы повторяем содержание п.13 лекции 1.

Определение. Пусть - произвольное непустое множество, элементы которого мы будем называть векторами, K – поле, элементы которого мы будем называть скалярами. Пусть на множестве определена внутренняя бинарная алгебраическая операция, которую мы будем обозначать знаком + и называть сложением векторов. Пусть также на множестве определена внешняя бинарная алгебраическая операция, которую мы будем называть умножением вектора на скаляр и обозначать знаком умножения. Другими словами определены два отображения:

;

.

Множество вместе с этими двумя алгебраическими операциями называется векторным пространством над полем К, если выполняются следующие аксиомы:

1. Сложение ассоциативно, т.е.

.

2. Существует нулевой вектор, т.е.

.

3. Для любого вектора существует противоположный ему:

.

Вектор у, противоположный вектору х, обычно обозначается –х, так что

.

4. Сложение коммутативно, т.е. .

5. Умножение вектора на скаляр подчиняется закону ассоциативности, т.е.

,

где произведение есть произведение скаляров, определенное в поле К.

6. , где 1 - это единица поля К.

7. Умножение вектора на скаляр дистрибутивно относительно сложения векторов:

.

8. Умножение вектора на скаляр дистрибутивно относительно сложения скаляров: .

Определение. Векторное пространство над полем вещественных чисел называется вещественным векторным пространством.

Теорема. (Простейшие свойства векторных пространств.)

1. В векторном пространстве существует единственный нулевой вектор.

2. В векторном пространстве любой вектор имеет единственный противоположный ему.

3. или .

4. .

Доказательство. 1) Единственность нулевого вектора доказывается также, как единственность единичной матриц и, вообще, как единственность нейтрального элемента любой внутренней бинарной алгебраической операции.

Пусть 0 – нулевой вектор векторного пространства V. Тогда . Пусть – еще один нулевой вектор. Тогда . Возьмем в первом случае , а во втором – . Тогда и , откуда следует, что , ч.т.д.

2а) Сначала мы докажем, что произведение нулевого скаляра на любой вектор равен нулевому вектору.

Пусть . Тогда, применяя аксиомы векторного пространства, получаем:

.

Относительно сложения векторное пространство является абелевой группой, а в любой группе справедлив закон сокращения. Применяя закон сокращения, из последнего равенства следует

.

2б) Теперь докажем утверждение 4). Пусть – произвольный вектор. Тогда

.

Отсюда сразу же следует, что вектор является противоположным вектору х.

2в) Пусть теперь . Тогда, применяя аксиомы векторного пространства, и получаем:

.

2г) Пусть и допустим, что . Так как , где К – поле, то существует . Умножим равенство слева на : , откуда следует или или .

Теорема доказана.

п.2. Примеры векторных пространств.

1) Множество числовых вещественных функций одной переменной, непрерывных на интервале (0; 1) относительно обычных операций сложения функций и умножения функции на число.

2) Множество многочленов от одной буквы с коэффициентами из поля K относительно сложения многочленов и умножения многочленов на скаляр.

3) Множество комплексных чисел относительно сложения комплексных чисел и умножения на действительное число.

4) Множество матриц одного и того же размера с элементами из поля К относительно сложения матриц и умножения матриц на скаляр.

Следующий пример является важным частным случаем примера 4.

5) Пусть - произвольное натуральное число. Обозначим через множество всех столбцов высоты n, т.е. множество матриц над полем K размера .

Множество является векторным пространством над полем К и называется арифметическим векторным пространством столбцов высоты n над полем K.

В частности, если вместо произвольного поля К взять поле действительных чисел , то векторное пространство называется вещественным арифметическим векторным пространством столбцов высоты n.

Аналогично, векторным пространством является и множество матриц над полем K размера или, иначе, строк длины n. Оно обозначается также через и также называется арифметическим векторным пространством строк длины n над полем K.

п.3. Системы векторов векторного пространства.

Определение. Системой векторов векторного пространства называют любое конечное непустое множество векторов этого пространства.

Обозначение: .

Определение. Выражение

, (1)

где - скаляры поля К, – векторы векторного пространства V, называется линейной комбинацией системы векторов . Скаляры называются коэффициентами этой линейной комбинации.

Определение. Если все коэффициенты линейной комбинации (1) равны нулю, то такую линейную комбинацию называют тривиальной, в противном случае – нетривиальной.

Пример. Пусть система из трех векторов векторного пространства V. Тогда

– тривиальная линейная комбинация данной системы векторов;

– нетривиальная линейная комбинация данной системы векторов, т.к. первый коэффициент этой комбинации .

Определение. Если какой-либо вектор х векторного пространства V может быть представлен в виде:

,

то говорят, что вектор х линейно выражается через векторы системы . В этом случае говорят также, что система линейно представляет вектор х.

Замечание. В этом и предыдущем определении слово "линейно" часто пропускают и говорят, что система представляет вектор или вектор выражается через векторы системы и т.п.

Пример. Пусть – система из двух столбцов арифметического вещественного векторного пространства столбцов высоты 2. Тогда столбец линейно выражается через столбцы системы или данная система столбцов линейно представляет столбец х. Действительно,

.

п.4. Линейно зависимые и линейно независимые системы векторов векторного пространства.

Так как произведение нулевого скаляра на любой вектор есть нулевой вектор и сумма нулевых векторов равна нулевому вектору, то для любой системы векторов выполняется равенство

. (2)

Отсюда следует, что нулевой вектор линейно выражается через векторы любой системы векторов или, говоря иначе, любая система векторов линейно представляет нулевой вектор.

Пример. Пусть . В этом случае нулевой столбец можно линейно выразить через столбцы системы не одним способом:

или

или

.

Чтобы различать эти способы линейного представления нулевого вектора введем следующее определение.

Определение. Если выполняется равенство

(3)

и при этом все коэффициенты , то говорят, что система представляет нулевой вектор тривиально. Если же в равенстве (3) хотя бы один из коэффициентов не равен нулю, тогда говорят, что система векторов представляет нулевой вектор нетривиально.

Из последнего примера мы видим, что существуют системы векторов, которые могут представлять нулевой вектор нетривиально. Из следующего примера мы увидим, что существуют системы векторов, которые не могут представлять нулевой вектор нетривиально.

Пример. Пусть – система двух столбцов из векторного пространства . Рассмотрим равенство:

,

где неизвестные пока коэффициенты. Используя правила умножения столбца на скаляр (число) и сложения столбцов, получаем равенство:

.

Из определения равенства матриц следует, что и .

Таким образом, данная система не может представлять нулевой столбец нетривиально.

Из приведенных примеров следует, что существует два вида систем векторов. Одни системы представляют нулевой вектор нетривиально, а другие нет. Отметим еще раз, что любая система векторов представляет нулевой вектор тривиально.

Определение. Система векторов векторного пространства, которая представляет нулевой вектор ТОЛЬКО тривиально называется линейно независимой.

Определение. Система векторов векторного пространства, которая может представить нулевой вектор нетривиально называется линейно зависимой.

Последнее определение можно дать в более развернутом виде.

Определение. Система векторов векторного пространства V называется линейно зависимой, если найдется такой ненулевой набор скаляров поля K

,

что

.

Замечание. Любая система векторов может представлять нулевой вектор тривиально:

.

Но этого недостаточно, чтобы выяснить линейно зависимая или же линейно независимая данная система векторов. Из определения следует, что линейно независимая система векторов не может представлять нулевой вектор нетривиально, а только тривиально. Поэтому для того, чтобы убедиться в линейной независимости данной системы векторов, нужно рассмотреть представление нуля произвольной линейной комбинацией этой системы векторов:

.

Если это равенство невозможно при условии, чтобы хотя бы один коэффициент этой линейной комбинации был ненулевой, тогда эта система является по определению линейно независимой.

Так в примерах предыдущего параграфа система столбцов является линейно независимой, а система столбцов является линейно зависимой.

Аналогично доказывается линейная независимость системы столбцов , , ... ,

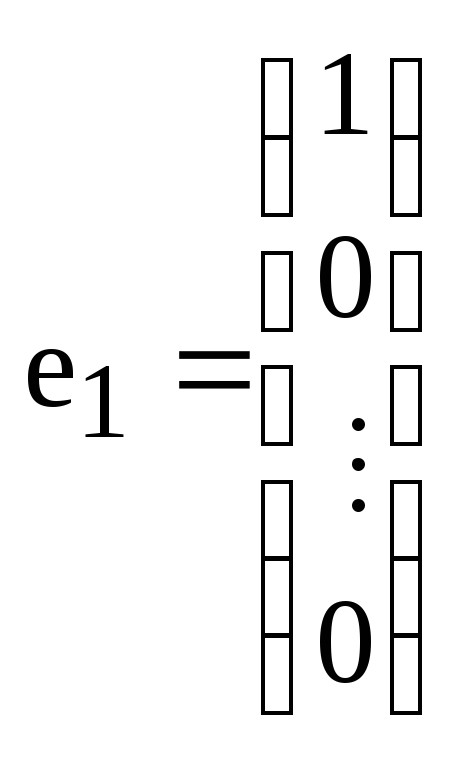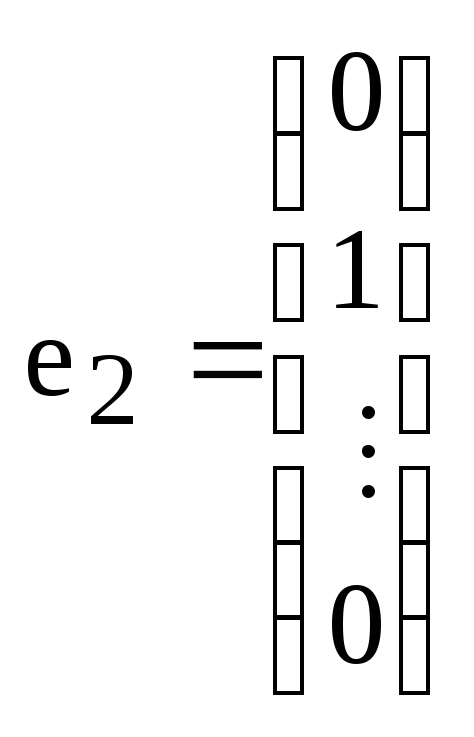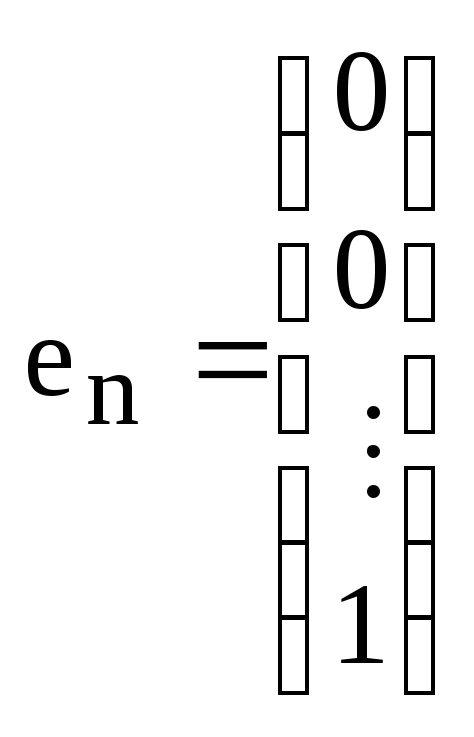
из пространства , где К - произвольное поле, n – произвольное натуральное число.

Следующие теоремы дают несколько критериев линейной зависимости и соответственно линейной независимости систем векторов.

Теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)

Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы.

Доказательство. Необходимость. Пусть система линейно зависимая. Тогда, по определению, она представляет нулевой вектор нетривиально, т.е. существует нетривиальная линейная комбинация данной системы векторов равная нулевому вектору:

,

где хотя бы один из коэффициентов этой линейной комбинации не равен нулю. Пусть , .

Разделим обе части предыдущего равенства на этот ненулевой коэффициент (т.е. умножим на :

.

Обозначим: , где .

Тогда

или ,

т.е. один из векторов системы линейно выражается через другие векторы этой системы, ч.т.д.

Достаточность. Пусть один из векторов системы линейно выражается через другие вектора этой системы:

.

Перенесем вектор в правую часть этого равенства:

.

Так как коэффициент при векторе равен , то мы имеем нетривиальное представление нуля системой векторов , что означает, что эта система векторов является линейно зависимой, ч.т.д.

Теорема доказана.

Следствие.

1. Система векторов векторного пространства является линейно независимой тогда и только тогда, когда ни один из векторов системы линейно не выражается через другие вектора этой системы.

2. Система векторов, содержащая нулевой вектор или два равных вектора, является линейно зависимой.

Доказательство.

1) Необходимость. Пусть система линейно независимая. Допустим противное и существует вектор системы линейно выражающийся через другие вектора этой системы. Тогда по теореме система является линейно зависимой и мы приходим к противоречию.

Достаточность. Пусть ни один из векторов системы не выражается через другие. Допустим противное. Пусть система линейно зависимая, но тогда из теоремы следует, что существует вектор системы линейно выражающийся через другие векторы этой системы и мы опять приходим к противоречию.

2а) Пусть система содержит нулевой вектор. Допустим для определенности, что вектор :. Тогда очевидно равенство

,

т.е. один из векторов системы линейно выражается через другие вектора этой системы. Из теоремы следует, что такая система векторов является линейно зависимой, ч.т.д.

Заметим, что этот факт можно доказать непосредственно из определения линейно зависимой системы векторов.

Так как , то следующее равенство очевидно

.

Это нетривиальное представление нулевого вектора, а значит система является линейно зависимой.

2б) Пусть система имеет два равных вектора. Пусть для определенности . Тогда очевидно равенство

, т.е. первый вектор линейно выражается через остальные векторы этой же системы. Из теоремы следует, что данная система линейно зависимая, ч.т.д.

Аналогично предыдущему это утверждение можно доказать и непосредственно определения линейно зависимой системы.

Действительно, так как , то верно равенство

,

т.е. мы имеем нетривиальное представление нулевого вектора.

Следствие доказано.

Теорема (О линейной зависимости системы из одного вектора.

Система, состоящая из одного вектора является линейно зависимой тогда и только тогда, когда этот вектор нулевой.

Доказательство.

Необходимость. Пусть система линейно зависимая, т.е. существует нетривиальное представление нулевого вектора

,

где и . Из простейших свойств векторного пространства следует, что тогда .

Достаточность. Пусть система состоит из одного нулевого вектора . Тогда эта система представляет нулевой вектор нетривиально

,

откуда следует линейная зависимость системы .

Теорема доказана.

Следствие. Система, состоящая из одного вектора является линейно независимой тогда и только тогда, когда этот вектор ненулевой.

Доказательство оставляется читателю как упражнение.