golovizin_lekcii_po_lineynoy_algebre_2_semestr / Лекция 27. Теорема о ранге матрицы

Головизин В.В. Лекции по алгебре и геометрии. Лекция 27. 6

Лекции по алгебре и геометрии. Семестр 2.

Лекция 27. Теорема о ранге матрицы.

Краткое содержание: линейные формы, ранг системы векторов, элементарные преобразования векторов системы, ранг матрицы, необходимые и достаточные условия обратимости квадратной матрицы, теорема о ранге матрицы.

п.1. Линейные формы.

Определение. Линейной формой (линейным функционалом) определенной на векторном пространстве V над полем K называется любое линейное отображение

.

Из определения следует, что отображение f обладает свойствами аддитивности и однородности, т.е.

, выполняются равенства:

и .

Замечание. Любое поле K само является векторным пространством над полем K, т.е. над самим собой. Его можно рассматривать как пространство столбцов высоты один. Тогда линейная форма есть линейное отображение векторных пространств или гомоморфизм. Можно применить общую теорию линейных отображений векторных пространств для этого частного случая и получить отсюда все нужные результаты. Но мы поступим иначе.

Теорема. (Общий вид линейной формы.)

Любая линейная форма относительно произвольного базиса векторного пространства V над полем K имеет вид:

, (1)

где – произвольный вектор, – координаты вектора х относительно данного базиса, , .

Доказательство. Пусть х – произвольный вектор. Разложим вектор х по базису :

. Тогда в силу линейности отображения f имеем:

.

Обозначая , , получаем равенство (1), ч.т.д.

Теорема доказана.

Теорема. Отображение , определенное равенством (1) является линейной формой.

Доказательство. Выберем и зафиксируем в пространстве V произвольный базис . Пусть – координаты вектора х относительно данного базиса. Выберем произвольным образом набор скаляров и положим по определению:

, . (2)

Тем самым мы определили отображение . Докажем, что отображение f является линейным.

1) Пусть – произвольные векторы, – произвольный скаляр. Пусть

, . Тогда ,

и

,

, ч.т.д.

Теорема доказана.

Замечание. Так как координаты базисного вектора в базисе есть набор скаляров (0, 0, …, 1, …0), где единственная единица стоит на k-м месте, то из равенства (2) следует, что .

Определение. Равенство

(3)

называется общим видом линейной формы от n переменных над полем K. Скаляры называются коэффициентами этой линейной формы.

Замечание. Равенство (3) определяет линейное отображение из пространства столбцов высоты n в поле К, т.е. определяет линейную форму на пространстве .

Определение. Набор скаляров образует матрицу – строку длины n. Эта матрица

называется матрицей линейной формы.

Если неизвестные линейной формы записать в виде столбца:

,

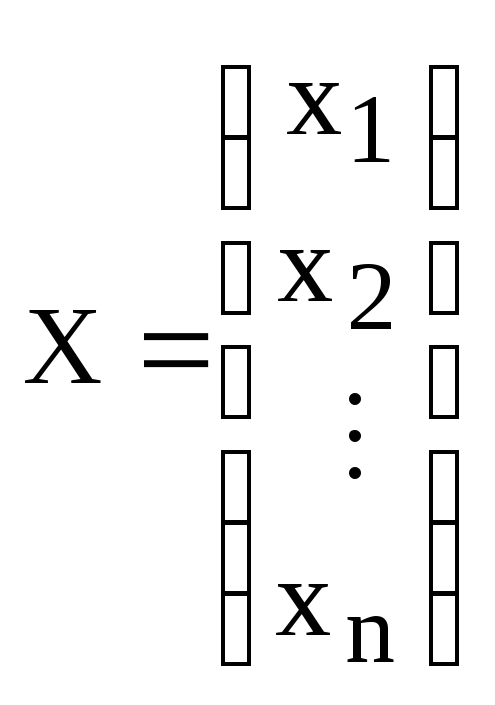тогда общий вид линейной формы можно записать в матричном виде:

.

Следствие. Пусть V – произвольное векторное пространство размерности n, в котором выбран и зафиксирован какой-нибудь базис. Тогда между всеми линейными формами, определенными на пространстве V и всеми строками длины n с элементами из поля K, существует взаимно однозначное соответствие.

Другими словами, любая строка длины n определяет на любом векторном пространстве размерности n линейную форму, матрицей которой она и является (относительно выбранного базиса).

Пример. Рассмотрим отображение , определенное правилом. Каждому столбцу из пространства поставим в соответствие его последнюю координату:

.

или иначе,

.

Очевидно, что это отображение является линейным и задается матрицей

и .

Замечание. Если взять поле R и столбцы высоты 3, то это отображение можно интерпретировать как проекцию вектора на ось аппликат Оz:

. Таким образом, проекции вектора как направленного отрезка на координатные оси есть примеры линейных форм, определенных на пространстве векторов как направленных отрезков.

п.2. Ранг системы векторов.

Пусть V – векторное пространство над полем K, – произвольная система векторов пространства V.

Определение. Любое непустое подмножество множества называют подсистемой данной системы векторов.

Пример. Пусть дана система векторов . Тогда , , – подсистемы данной системы. Сама система тоже является подсистемой самой себя.

Определение. Подсистему называют максимальной линейно независимой подсистемой данной системы векторов, если она линейно независимая и при добавлении к ней любого вектора данной системы становится линейно зависимой.

Определение. Рангом системы векторов называют число векторов в ее максимальной линейно независимой подсистеме.

Обозначение: .

Заметим, что если система векторов содержит хотя бы один ненулевой вектор, то ее ранг больше или равен 1.

В дальнейшем предполагаем, что система векторов содержит ненулевой вектор.

Следующая теорема показывает, что ранг системы является ее инвариантом, т.е. не зависит от выбора максимальной линейно независимой подсистемы данной системы векторов.

Теорема. (О ранге системы векторов.) Ранг системы векторов равен размерности линейной оболочки, натянутой на ее векторы, т.е.

. (4)

Доказательство. Для удобства записи перенумеруем векторы системы так, чтобы система была максимальной линейно независимой подсистемой данной системы векторов. Тогда .

Рассмотрим два случая.

1) , т.е. данная система векторов является линейно независимой. Тогда она сама является ее максимальной линейно независимой подсистемой и ее ранг равен m. Рассмотрим линейную оболочку, натянутую на векторы данной системы:

.

Система векторов по определению линейной оболочки является ее порождающей системой и по нашему предположения является линейно независимой. Следовательно, система является базисом линейной оболочки L, а потому ее размерность равна m и равенство (4) доказано.

2) . Тогда система векторов является линейно зависимой для всех значений индекса , откуда следует, что вектор линейно выражается через предыдущие векторы этой системы, т.е. . Отсюда следует, что

,

п так как обратное включение очевидно, то

,

и , ч.т.д.

Теорема доказана.

Следствие. Ранг системы векторов является ее инвариантом, т.е. на зависит от выбора ее максимальной линейно независимой подсистемы.

Доказательство. Пусть произвольная система векторов и , – две ее произвольные максимальные линейно независимые подсистемы. Тогда, по теореме,

и

, откуда

, ч.т.д.

Следствие доказано.

Замечание. Из последней теоремы следует, что базисом линейной оболочки, натянутой на систему векторов является максимальная линейно независимая подсистема данной системы векторов. Действительно, найденная максимальная линейно независимая подсистема является линейно независимой и число векторов в ней равно размерности линейной оболочки, т.е. она является базисом линейной оболочки.

п.3. Элементарные преобразования системы векторов.

Определение. Следующие преобразования системы векторов называются элементарными:

1) любая перестановка векторов системы;

2) умножение любого вектора системы на ненулевой скаляр;

3) прибавление к любому вектору системы любой линейной комбинации любых других векторов системы;

4) удаление нулевого вектора из системы.

Теорема. Элементарные преобразования системы векторов не изменяют ее ранга.

Доказательство.

1) Пусть дана система векторов и – ее некоторая максимальная линейно независимая подсистема, т.е. базис линейной оболочки . Пусть – любая перестановка данной системы векторов и – ее произвольная максимальная линейно независимая подсистема. Но эта подсистема будет и подсистемой системы , т.е. также будет базисом линейной оболочки . Отсюда следует, что , ч.т.д.

2) Пусть дана система векторов . Умножим, для определенности вектор на скаляр и получим систему . Легко видеть, что

.

Действительно,

,

откуда следует, что и .

Обратно, пусть . Тогда,

, т.е.

, откуда следует, что

.

Из этого равенства следует, что равны их размерности

.

Применяя теорему о ранге системы векторов, получаем, что , ч.т.д.

3) Пусть дана система векторов . Для определенности, прибавим к первому вектору системы произвольную линейную комбинацию других векторов этой системы и получим новую систему векторов:

. Как и в предыдущем пункте доказательство легко показать, что

.

Действительно, пусть

. Тогда,

, т.е.

.

Обратно, пусть

. Тогда,

, ч.т.д.

4) Пусть дана система векторов . Очевидно, что , откуда, и

, ч.т.д.

Теорема доказана.

Замечание. Эта теорема широко используется при вычислении ранга системы строк или столбцов пространства .

п.4. Ранг матрицы.

Пусть А – произвольная матрица размеров над полем К и пусть натуральное число k такое, что оно не превосходит ни числа строк матрицы А, ни числа ее столбцов, т.е. .

Определение. Минором – го порядка матрицы А называют определитель матрицы – го порядка, которая получается из матрицы А вычеркиванием всех строк и столбцов, кроме отмеченных произвольным образом строк и столбцов.

Пример. 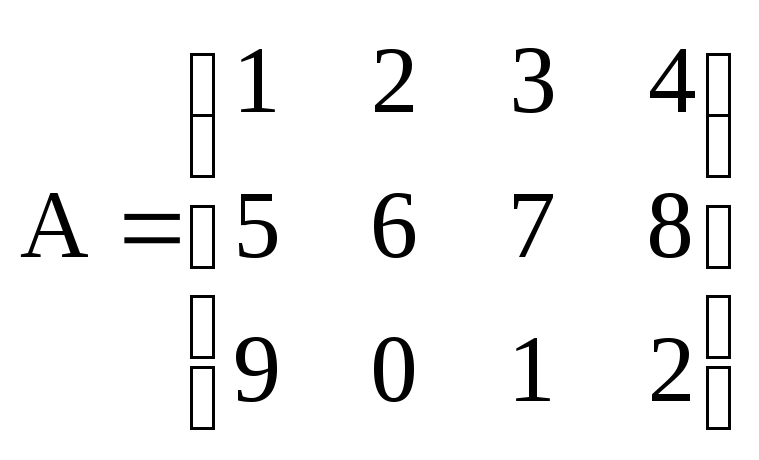. Отметим 1-й и 4-й столбцы и первые две строки, а остальные (2-й и 3-й столбец и 3-ю строку) вычеркнем: – минор второго порядка матрицы А.

Или вычеркнем любой столбец матрицы А, например третий:

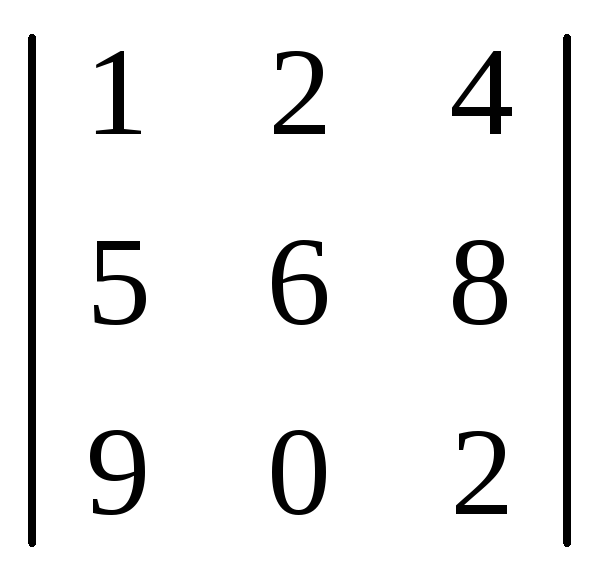– минор третьего порядка матрицы А.

Ясно, что минором первого порядка является любой ее элемент, а миноров четвертого порядка не существует, миноров третьего порядка существует ровно четыре, а миноров второго порядка ровно 18 штук.

Определение. Рангом ненулевой матрицы называется максимальный порядок ее ненулевого минора.

Обозначение: .

Ранг нулевой матрицы по определению полагают равным нулю.

Замечание. Из определения следует, что ранг ненулевой матрицы есть натуральное число, не превышающее ни числа строк, ни числа столбцов. Так в примере выше ранг матрицы А может быть равен 1 или 2 или 3. Так как минор второго порядка , то ранг матрицы равен 2, если все 4 ее минора третьего порядка равны 0, и равен 3, если среди ее миноров третьего порядка найдется хотя бы один ненулевой.

Пусть А – произвольная матрица размеров над полем K. Тогда ее строки имеют длину n и могут рассматриваться как векторы арифметического векторного пространства строк длины n: .

Столбцы матрицы А имеют высоту m и могут рассматриваться как векторы арифметического векторного пространства столбцов высоты m: .

Обозначим – систему строк матрицы А, – систему ее столбцов. Тогда для всех и для всех . Эти системы, как и любые системы векторов векторного пространства имеют свой ранг.

Обозначим:

, ,

Теорема. (О ранге матрицы.) Ранг матрицы равен рангу системы ее строк и равен рангу системы ее столбцов.

Иначе, в наших обозначениях: .

Для доказательства этой теоремы нам потребуются две леммы:

Лемма 1. Пусть А – квадратная матрица – го порядка над полем K. Следующие утверждения равносильны:

1) система строк матрицы А – линейно зависимая;

2) система столбцов матрицы А – линейно зависимая;

3) определитель матрицы А равен нулю.

Доказательство. . Это следует из свойств определителя и уже доказано.

. Пусть . Нам нужно доказать, что система столбцов матрицы А является линейно зависимой.

Допустим противное. Пусть система столбцов – линейно независимая. Так как А – квадратная матрица, то все ее столбцы имеют высоту n, т.е. являются векторами пространства , размерность которого равна n. Следовательно, система является базисом пространства .

Пусть – канонический базис пространства , т.е.

, , …, .

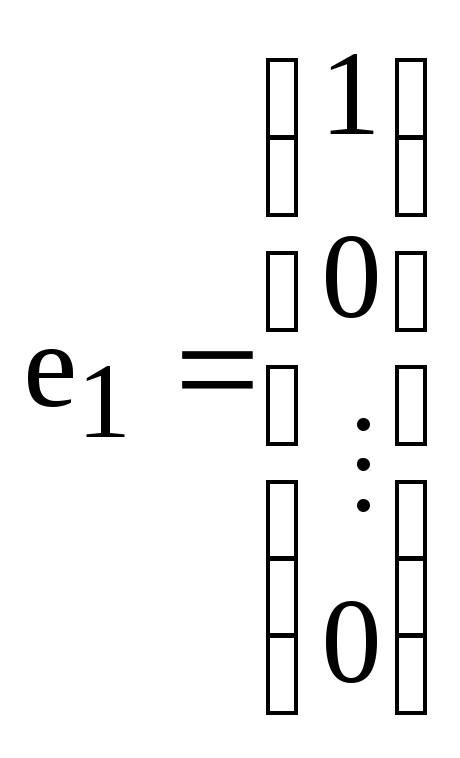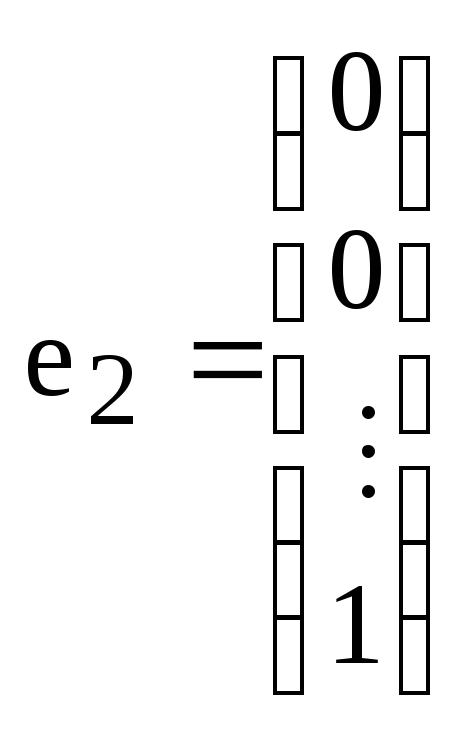Найдем матрицу перехода от канонического базиса к базису из столбцов матрицы А. Для этого разложим векторы базиса по каноническому базису. В матричной форме эти разложения будут иметь вид:

, где С – матрица перехода. Но последнее равенство есть равенство: , где Е – единичная матрица, откуда следует, что . Так как матрица перехода является невырожденной, т.е. , то отсюда следует, что , что противоречит условию . Следовательно, наше предположение о линейной независимости системы столбцов матрицы А является неверным, ч.т.д.

. Из доказанного следует, что система строк матрицы А является линейно зависимой тогда и только тогда, когда , т.к. строки матрицы А являются столбцами транспонированной матрицы . Так как , то все доказано.

Теорема доказана.

Следствие. Пусть А – квадратная матрица – го порядка над полем К. Следующие утверждения равносильны:

1) система строк матрицы А – линейно независимая;

2) система столбцов матрицы А – линейно независимая;

3) определитель матрицы А не равен нулю.

Лемма 2. Пусть – подпространство пространства V над полем K и . Тогда существует ненулевая линейная форма , такая, что , т.е. , .

Доказательство. Пусть – базис подпространства L. Дополним его до базиса пространства V: . Определим на V линейную форму с помощью равенства

, .

Как мы уже видели выше, это отображение есть линейная форма, причем ненулевая, т.е., например,

.

Пусть – произвольный вектор подпространства L. Разложим его по базису V:

, откуда следует, что , ч.т.д.

Лемма доказана.

п.4. Вычисление ранга матрицы и нахождение базиса линейной оболочки ее системы строк (столбцов).

Для вычисления ранга матрицы часто применяют метод Гаусса приведения матрицы к ступенчатому виду. Метод Гаусса основан на элементарных преобразованиях строк матрицы, которые, как мы уже знаем, не изменяют ранга системы строк, а значит не изменяют и ранга матрицы.

Таким образом, ранг данной матрицы равен рангу получившейся после преобразований ступенчатой матрицы. В свою очередь, ранг ступенчатой матрицы легко вычисляется, так как легко увидеть ее максимальный ненулевой минор и его порядок.

Пример. Вычислить ранг матрицы и найти базис и размерность линейной оболочки натянутой на ее столбцы.

Решение.

1-й шаг: умножим первую строку на 2 и прибавим ко второй строке:

;

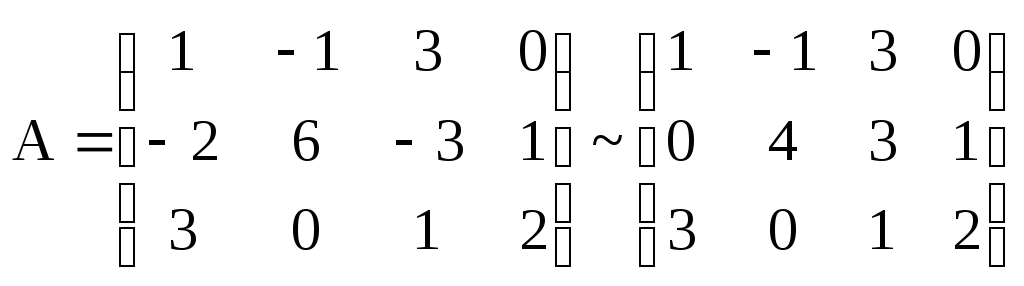2-й шаг: прибавим к третьей строке первую, умноженную на (–3):

;

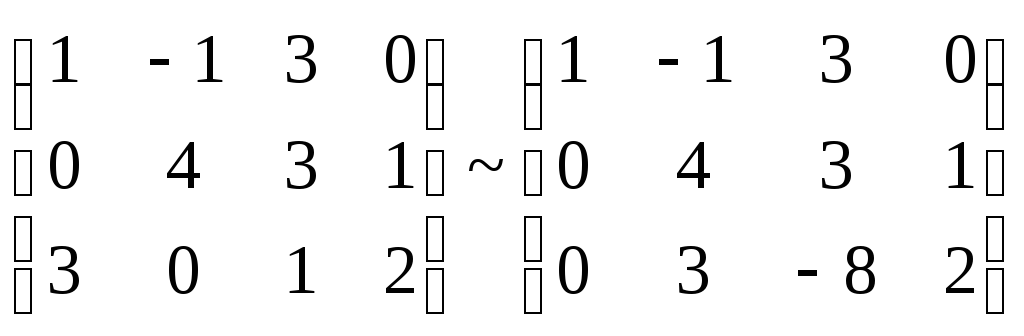3-й шаг: прибавим ко второй строке 3-ю, умноженную на (–1):

;

4-й шаг: умножаем вторую строку на (–3) и прибавляем к третьей строке:

.

Ранг последней матрицы равен 3, так как в первых трех столбцах стоит ненулевой минор 3-го порядка

, а миноров 4-го порядка не существует.