golovizin_lekcii_po_lineynoy_algebre_2_semestr / Лекция 28. Системы линейных уравнений
.docГоловизин
В.В. Лекции по алгебре и геометрии.
Лекция 28.
Лекции по алгебре и геометрии. Семестр 2.
Лекция 28. Системы линейных уравнений.
Краткое содержание: линейное уравнение с несколькими неизвестными, система линейных уравнений с несколькими неизвестными, матрица системы, столбец свободных членов, расширенная матрица системы, столбец неизвестных, матричная и векторная формы записи системы линейных уравнений, решение системы линейных уравнений, однородные и неоднородные системы, классификация систем по множеству решений, теорема Кронекера-Капелли, пространство решений системы и его размерность, структура множества решений неоднородной системы линейных уравнений, необходимые и достаточные условия определенности совместной системы, необходимое и достаточное условие определенности квадратной системы линейных уравнений, формулы Крамера, понятие линейного многообразия, геометрический смысл множества решений системы линейных уравнений.
п.1. Основные определения.
Определение. Уравнение вида
,
(1)
где
–
действительные числа,
– переменные (неизвестные), называется
линейным уравнением с n
неизвестными.
Определение.
Числа
в уравнении (1) называются коэффициентами
линейного уравнения, число
в уравнении (1) называется свободным
членом линейного уравнения.
Определение. Уравнение вида
называется однородным линейным уравнением с n неизвестными.
Пусть дана система из m линейных уравнений с n неизвестными:
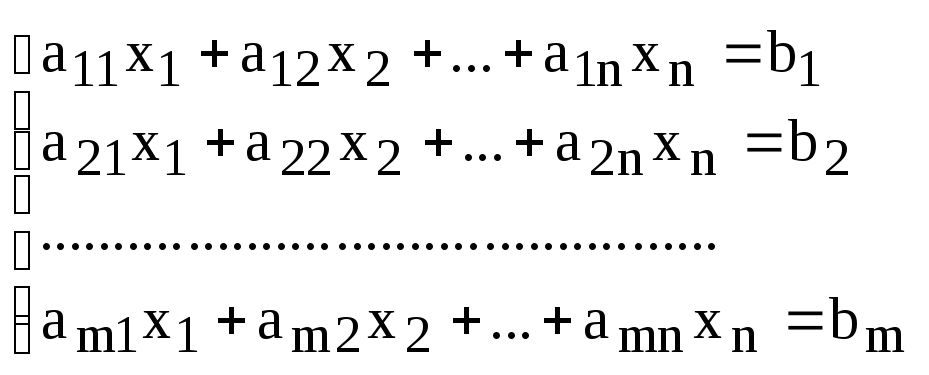(2)
Здесь, по вполне понятным причинам, коэффициенты линейных уравнений снабжены нижними двойными индексами. Они образуют матрицу
.
(3)
Определение. Матрица А, элементами которой являются соответствующие коэффициенты линейных уравнений системы называется матрицей этой системы.
Определение.
Столбец
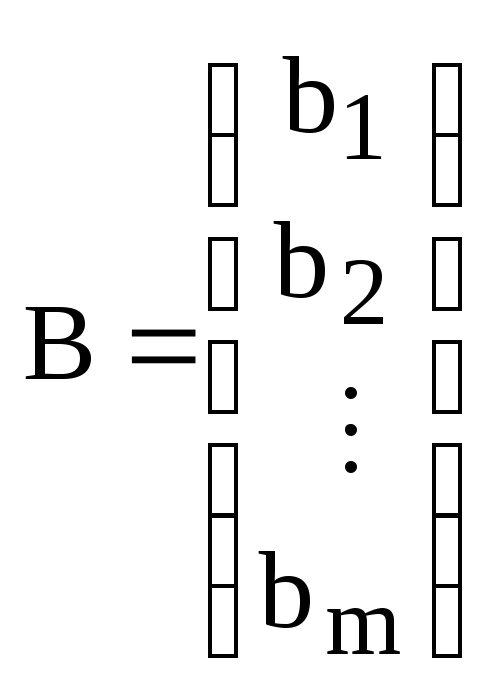называется столбцом свободных членов
системы (2).
Определение 4. Матрица
называется
расширенной матрицей системы (2) и
обозначается
.
Определение.
Столбец
называется столбцом неизвестных системы
(2).
Определение. Система линейных уравнений называется однородной, если каждое уравнение системы является однородным.
Другими словами, систему линейных уравнений называют однородной, если столбец свободных членов системы является нулевым.
Замечание. Уравнение
(1) можно рассматривать как частный
случай системы (2) при
и тоже можно называть системой линейных
уравнений, состоящей из одного уравнения
и n неизвестных.
Определение. Решением системы линейных уравнений с n неизвестными называется упорядоченный набор из n чисел, которые будучи подставлены в систему, обращают каждое уравнение системы в верное числовое равенство.
Обозначение:
или
.
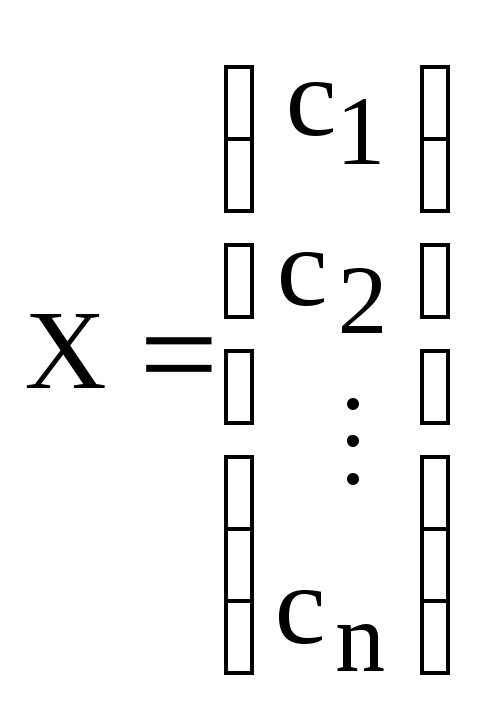В первом случае говорят о строке решений,
во втором – о столбце решений.
п.2. Способы записи системы линейных уравнений.
Про систему вида (2) говорят, что она записана в развернутом виде. Или говорят, что система записана в скалярной форме.
Если воспользоваться правилом умножения матриц и определением равенства матриц, то систему линейных уравнений можно записать в матричной форме:
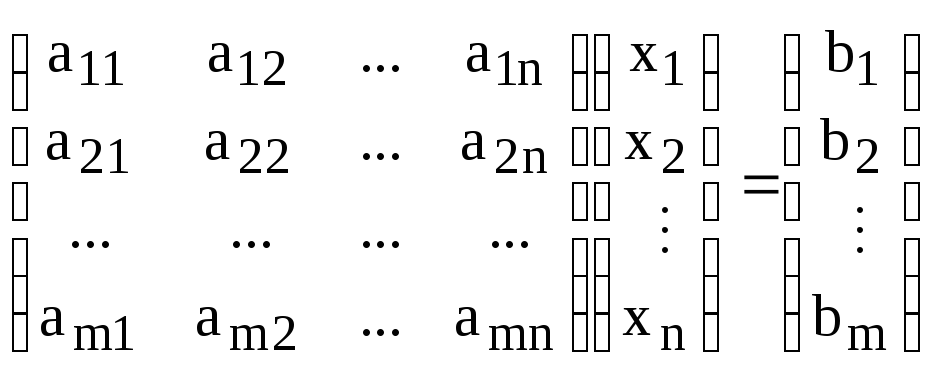или
.
Обозначим
–
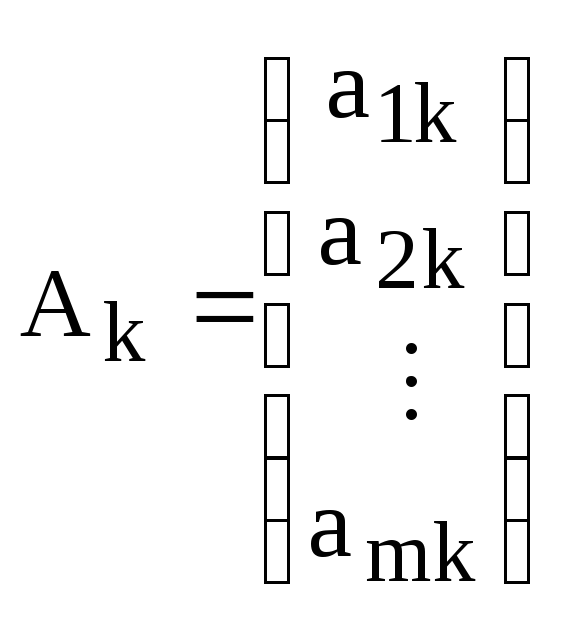-й
столбец матрицы А. Тогда систему (2) можно
записать в виде:
.
Такую форму записи системы линейных уравнений мы будем называть векторной, т.к. в этом равенстве столбец В представлен в виде линейной комбинации столбцов матрицы системы. А столбец есть вектор векторного пространства столбцов соответствующей высоты.
п.3. Классификация систем линейных уравнений.
Системы различаются по внешнему виду и в этом случае их называют так же, какова их матрица коэффициентов: квадратная, треугольная, диагональная, ступенчатая и т.п.
Системы классифицируют и по множеству их решений.
Определение. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение и несовместной в противном случае.
Совместные системы также классифицируют по множеству решений.
Определение. Совместная система линейных уравнений называется определенной, если она имеет единственное решение и неопределенной, если она имеет более одного решения.
Замечание. Легко
видеть, что однородная система линейных
уравнений
является совместной, т.к. она всегда
имеет нулевое решение.
п.4. Необходимые и достаточные условия совместности системы линейных уравнений.
Теорема (Кронекер – Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.
Другими словами,
если
–
система линейных уравнений, то для того,
чтобы данная система имела хотя бы одно
решение необходимо и достаточно, чтобы
.
Доказательство. 1) Необходимость.
Запишем систему в векторной форме:
.
Если
система совместна, то существует хотя
бы одно ее решение:
и верно равенство:
,
которое означает, что
,
откуда следует, что
.
Так
как включение
очевидно, то отсюда следует равенство
,
а значит равны их размерности
.
Так как размерность линейной оболочки системы векторов равно рангу этой системы, то
,
откуда по теореме о ранге матрицы
.
2) Достаточность.
Пусть
.
Тогда по теореме о ранге матрицы равны
ранги систем их столбцов:
,
откуда следует равенство размерностей линейных оболочек, натянутых системы их столбцов:
.
Так
как
,
то из равенства их размерностей следует,
что линейные оболочки равны:
,
откуда следует, что
,
т.е. столбец В представим в виде линейной комбинации столбцов матрицы А:
,
что, в свою очередь, означает, что набор скаляров
является решением
данной системы, т.е. система является
совместной, ч.т.д.
Теорема доказана.
п.5. Пространство решений однородной системы линейных уравнений.
Прежде всего
заметим, что однородная система линейных
уравнений
всегда является совместной, т.к. всегда
имеется нулевое решение
–
нулевой столбец неизвестных.
Теорема. Множество решений однородной системы линейных уравнений является векторным пространством.
Доказательство.
Пусть
– однородная система m
линейных уравнений с n
неизвестными. Тогда решением системы
является столбец неизвестных X,
который мы рассматриваем как вектор из
пространства столбцов высоты n:
,
где K– поле коэффициентов
системы.
Таким образом,
множество решений системы
есть множество столбцов из пространства
столбцов
,
для которых верно матричное равенство
.
Как мы видели ранее (см. лекцию 26) это множество является ядром матрицы А:
.
Мы
уже знаем, что ядро матрицы является
векторным подпространством пространства
столбцов
,
а следовательно и само является векторным
пространством.
Теорема доказана.
Замечание.
В дальнейшем множество решений однородной
системы линейных уравнений
мы будем называть пространством решений
этой однородной системы линейных
уравнений и обозначать
.
Теорема (О размерности пространства решений однородной системы линейных уравнений.)
Пусть
– однородная система m
линейных уравнений с n
неизвестными и
–
пространство ее решений. Тогда
.
Иначе, размерность пространства решений однородной системы линейных уравнений равна числу неизвестных системы минус ранг ее матрицы.
Обозначим для
краткости
.
Тогда теорема утверждает, что верно
равенство:
.
Доказательство. По теореме о ядре и образе линейного отображения (см. лекцию 26, п.4)
,
или
в наших обозначениях:
и
,
откуда следует, что
.
В той же лекции 26, п.4. мы установили, что
.
В лекции 27 п.2. было доказано, что размерность линейной оболочки системы векторов равна рангу этой системы, т.е. в наших обозначениях:
.
По теореме о ранге матрицы (см. лекцию 27, п.4), ранг системы столбцов матрицы равен рангу этой матрицы:
.
Отсюда
следует, что
и
,
ч.т.д.
Теорема доказана.
Пусть
–
базис пространства
.
Тогда
–
линейная оболочка,
натянутая на систему базисных векторов
пространства
.
Напомним, что любое векторное пространство можно записать в виде линейной оболочки, натянутой на систему его базисных векторов.
Определение.
Базис
пространства решений
однородной системы линейных уравнений
называется фундаментальной системой
ее решений.
Так
как любой вектор векторного пространства
можно разложить по его базису, то любое
решение однородной системы
можно представить в виде линейной
комбинации ее фундаментальной системы
решений:
,
где
.
Определение.
Решение системы
,
записанное в виде
,
где
–
фундаментальная система решений, а
– произвольные постоянные (скаляры из
поля
),
называется ее общим решением.
Пример.
Решить систему:
.
Решение. Здесь
дана система из одного уравнения с двумя
неизвестными
и
.
Матрица системы имеет вид
и ее ранг
.
Тогда размерность
пространства решений
.
Следовательно, базис пространства решений данной системы (или иначе, фундаментальная система решений) состоит из одного ненулевого решения данной системы:
.
Заметим, что в
любом базисе нет нулевого вектора, так
что
.
В
данном случае одно ненулевое решение
легко найти подбором, например:
,
т.е. столбец этого решения:
.
Следовательно,
множество решений данной системы можно
записать в виде линейной оболочки,
натянутой на базисный вектор:
.
Общее решение данной системы имеет вид:
,
где с – любое действительное число.
Мы молчаливо предполагали, что полем коэффициентов данной системы является поле действительных чисел.
Ответ:
,
.
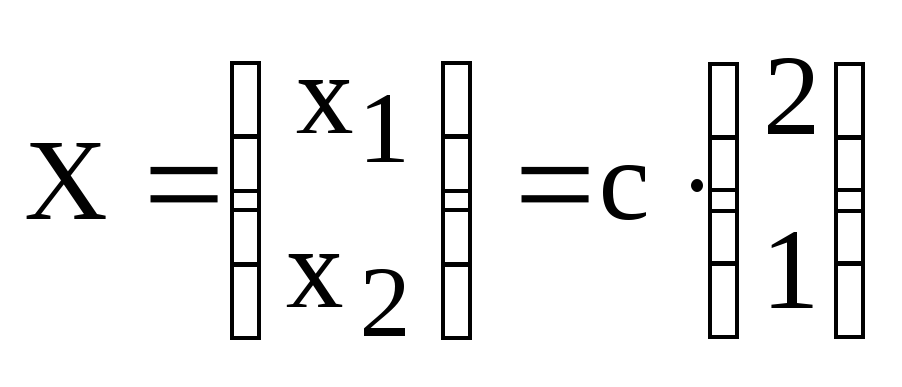Замечание.
Легко выполнить проверку. Подставляя
в данную систему
,
получаем:
,
т.е. уравнение превращается в верное
числовое равенство для любого
действительного числа с, что и требовалось
доказать.
п.6. Структура множества решений совместной неоднородной системы линейных уравнений.
Определение.
Пусть
–
неоднородная система линейных уравнений
с матрицей системы А. Система линейных
уравнений
называется однородной системой линейных
уравнений соответствующей данной
неоднородной системе линейных уравнений.
Определение.
Произвольное решение неоднородной
системы
называют ее частным решением.
Пример.
Найти частное решение системы
.
Решение. Легко видеть, что
или
или
– частные решения данной системы.
Ответ:
.
Обозначим через
множество всех решений неоднородной
системы
,
т.е.
,
а через
пространство решений соответствующей
однородной системы
.
Произвольное частное решение неоднородной
системы обозначим через X*,
так что
и верно равенство:
.
В этих обозначениях справедлива следующая теорема.
Теорема. (О структуре множества решений неоднородной системы.)
1)
Сумма любого частного решения
неоднородной системы
и любого решения
соответствующей однородной системы
является решением неоднородной системы
.
2)
Любое решение
неоднородной системы
можно представить в виде суммы некоторого
частного решения неоднородной системы
и некоторого решения соответствующей
однородной системы
.
Другими словами:
1)
если
и
,
то
;
т.е.
если
и
,
то
;
2)
если
и
,
то
,
т.е. любое решение
неоднородной системы можно представить
в виде
,
где
,
а
.
Доказательство.
1) Пусть
и
.
Тогда по свойствам сложения матриц
,
ч.т.д.
2)
Пусть
и
.
Тогда
,
т.е.
.
Обозначим
.
Тогда
,
где
,
а
,
ч.т.д.
Теорема доказана.
Введем обозначение:
.
Это
множество называется суммой подпространства
и вектора (столбца)
и еще оно называется линейным (или
векторным) многообразием, параллельным
подпространству
.
(См. ниже п.7.)
Как
видно из этого обозначения,
Используя это и предыдущие обозначения, последнюю теорему можно сформулировать следующим образом:
Теорема. (О структуре множества решений неоднородной системы.)
.
Иначе, множество
S решений неоднородной
системы
равно сумме подпространства решений
соответствующей однородной системы
и
произвольного частного решения X*
исходной неоднородной системы.
Следствие.
Любое решение неоднородной системы
линейных уравнений
может быть записано в виде:
,
где
–
общее решение соответствующей однородной
системы
,
а
– произвольное частное решение
неоднородной системы
.
Определение.
Решение неоднородной системы линейных
уравнений
,
записанное в виде
,
где
– произвольные постоянные (скаляры из
поля
),
–
фундаментальная система решений
соответствующей однородной системы
,
называется общим решением неоднородной
системы.
Вывод. Решить неоднородную систему линейных уравнений означает найти множество всех ее решений. А, в свою очередь, множество всех ее решений имеет вид:
.
Следовательно, в ответе достаточно
выписать общее решение:
.
Пример.
Решить систему:
.
Сначала,
любым способом находим произвольное
ее частное решение, например:
,
так, что
.
Общее решение соответствующей однородной
системы
мы уже нашли:
.
Тогда общее решение данной неоднородной
системы имеет вид:
.
Ответ:
,
.
п.7. Линейные (векторные) многообразия.
Пусть
–
произвольное подпространства пространства
и пусть
–
произвольный фиксированный вектор
пространства
(вообще говоря,
,
хотя это и не обязательно). Множество
векторов вида
,
где
обозначим через
,
т.е.
.
Легко видеть, что
если
,
то
,
а если
,
то
.
Более того, в этом случае множество
не является векторным подпространством
(т.к. не содержит нулевого вектора).
Определение.
Множество
при
называется линейным (векторным)
многообразием, параллельным подпространству
.
Пример.
Пространство столбцов высоты 2 с
действительными элементами:
можно интерпретировать как пространство
радиус-векторов точек координатной
плоскости, т.е. векторов, начало которых
находится в начале координат, а конец
в соответствующей точке плоскости.
Если же точку плоскости и ее радиус-вектор отождествить, то под словом вектор можно понимать точку плоскости.