golovizin_lekcii_po_lineynoy_algebre_2_semestr / Лекция 26. Линейные отображения
.docГоловизин
В.В. Лекции по алгебре и геометрии.
Лекция 26.
Лекции по алгебре и геометрии. Семестр 2.
Лекция 26. Линейные отображения векторных пространств.
Краткое содержание: определение линейного отображения (гомоморфизма) векторных пространств, примеры и их простейшие свойства, ядро и образ линейного отображения, теорема о размерности ядра и образа, матрица линейного отображения и ее изменение при изменении базиса, векторное пространство гомоморфизмов, линейный оператор (эндоморфизм) и его матрица, кольцо эндоморфизмов, матрица как форма задания линейного отображения.
п.1. Линейное отображение векторных пространств.
Определение.
Пусть V и W
– произвольные векторные пространства
над полем K. Отображение
называется линейным отображением или
гомоморфизмом векторного пространства
V в векторное пространство
W, если оно обладает
свойствами:
1)
свойство аддитивности:
,
;
2)
свойство однородности:
,
.
Если, кроме этого, гомоморфизм f является биекцией, то он называется изоморфизмом векторных пространств V и W.
Определение.
Если существует изоморфизм
,
то векторные пространства V
и W называются изоморфными.
Обозначение изоморфных векторных пространств:
.
Теорема. Отношение изоморфизма на множестве всех векторных пространств над полем K является отношением эквивалентности.
Доказательство оставляется читателю.
Обозначение.
Пусть V и W – произвольные фиксированные векторные пространства над полем K.
Множество
всех линейных отображений (гомоморфизмов)
из пространства V в
пространство W обозначается
или просто
.
Определение.
Линейное отображение из векторного
пространства V в себя:
называется линейным оператором или
эндоморфизмом векторного пространства
V. Биективный эндоморфизм
называется автоморфизмом векторного
пространства V.
Обозначение.
Множество всех
линейных операторов (эндоморфизмов)
векторного пространства V
над полем K обозначается
или
.
Множество всех автоморфизмов векторного
пространства V обозначается
.
Говорят также, что линейный оператор действует на векторном пространстве V.
п.2. Примеры линейных отображений.
Пример 1. Пусть V и W – произвольные векторные пространства над полем K. Зададим отображение
с
помощью правила:
положим
.
Это отображение называется нулевым отображением.
Очевидно, что нулевое отображение векторного пространства V в векторное пространство W является линейным, поэтому оно называется нулевым гомоморфизмом.
Пример 2. Зададим отображение
с
помощью правила:
положим
.
Это отображение называется тождественным отображением (тождественным оператором) векторного пространства V в себя.
Легко проверить, что тождественное отображение векторного пространства V в себя является линейным.
Действительно,
,
.
Отсюда,
и
.
Тождественный оператор называется также тождественным или единичным эндоморфизмом и часто обозначается буквой Е.
Пример
3. Пусть А – матрица размера
над полем K,
и
– арифметические векторные пространства
столбцов высоты
и
соответственно над полем K.
Устроим отображение
с
помощью правила:
положим
.
Проверим, что
данное отображение является линейным.
Пусть
.
Тогда
.
Здесь мы воспользовались свойствами действий с матрицами, а именно законом дистрибутивности умножения матриц относительно их сложения.
Далее,
,
.
Таким образом,
умножение матрицы на столбец соответствующей
высоты обладает свойствами аддитивности
и однородности и, следовательно, является
линейным отображением (линейным
оператором, если
).
Пример
4. Пусть V – произвольное
векторное пространство над полем K
размерности n и
–пространство столбцов высоты n.
Зафиксируем в пространстве V
какой-нибудь базис. Отображение
,
которое
каждому вектору
ставит в соответствие упорядоченный
набор
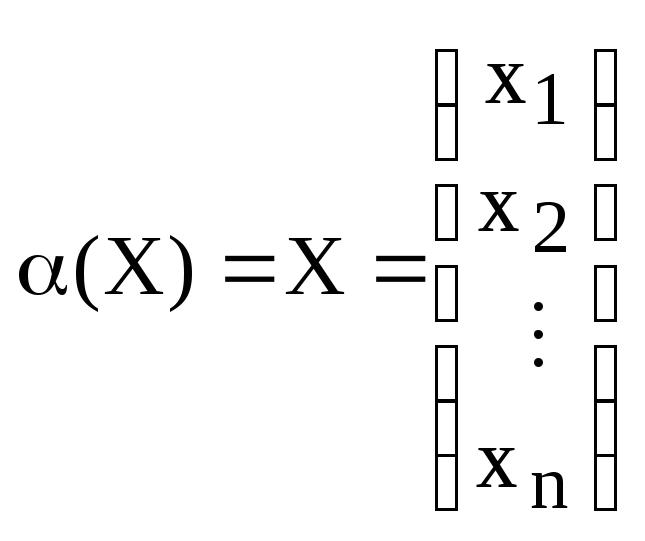
его координат относительно данного базиса является биективным линейным отображением или изоморфизмом векторных пространств. (См. лекцию 24.)
Пример
5. Пусть
–
множество векторов на плоскости, как
направленных отрезков. Устроим отображение
по правилу:
каждому
вектору
поставим в соответствие вектор
,
который получается из вектора
поворотом вокруг своего начала на угол
против часовой стрелки.
В наших обозначениях:
.
Легко
видеть, что это отображение является
линейным:
,
,
и
.
(Чтобы увидеть это, сложите два вектора по правилу параллелограмма и поверните полученный параллелограмм на заданный угол против часовой стрелки. Аналогично проверяется свойство однородности.)
Таким образом, данное отображение является линейным оператором, который называют оператором поворота на заданный угол в пространстве векторов на плоскости.
п.3. Простейшие свойства линейных отображений.
Теорема.
Пусть
линейное отображение векторного
пространства V в векторное
пространство W над полем
K. Тогда справедливы
следующие утверждения:
1)
;
2)
,
;
3)
,
,
.
Доказательство оставляется читателю.
Замечание. При
проверке линейности отображения, полезно
проверять свойство (1):
,
т.к. оно легко проверяется и если оно не
выполняется, то данное отображение не
является линейным. Например, отображение
из пространства столбцов высоты 2 в себя
по правилу:
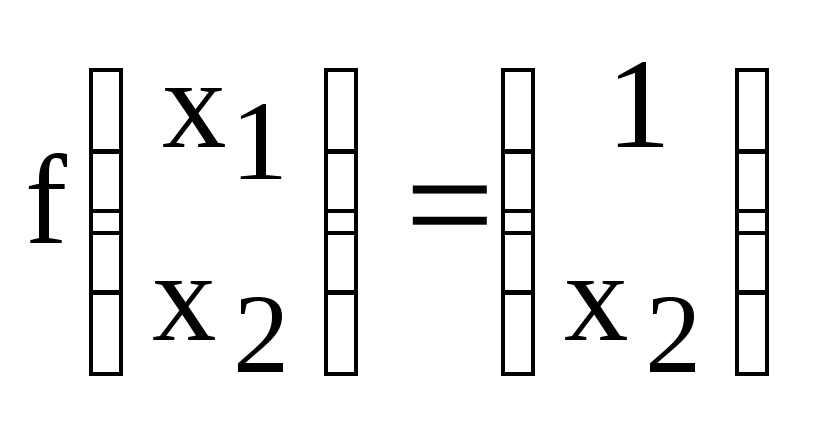
не является линейным, т.к.
.
п.4. Ядро и образ линейного отображения.
Определение.
Пусть
линейное отображение векторных
пространств. Ядром линейного отображения
f называется множество:
.
Образом линейного отображения f называют множество:
.
Другими словами, ядро линейного отображения состоит из векторов пространства V, которые отображаются в нулевой вектор пространства W, а образ линейного отображения это просто множество значений функции f.
Если f – линейный оператор, то говорят об ядре и образе линейного оператора.
Найдем ядро и образ линейных отображений, рассмотренных в примерах пункта 2.
Пример
1. Так как нулевое отображение
все векторы пространства
отображает в нулевой вектор пространства
,
то из определения ядра и образа линейного
отображения сразу же следует, что
и
.
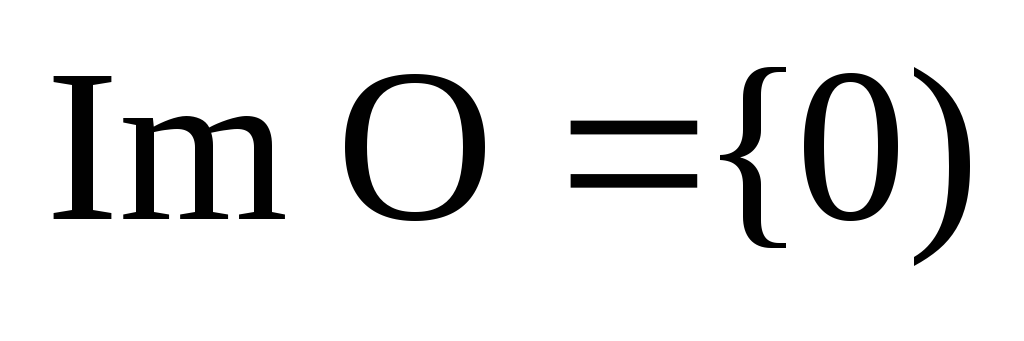Пример
2. Пусть
:
,
.
Тогда, очевидно,
.
Пример
3. Пусть
:
,
,
где А – матрица размера
над полем
.
Тогда,
–
множество решений
однородной системы из
линейных уравнений с
неизвестными, где А – матрица коэффициентов
системы;
.
Изучим это множество
подробнее. Обозначим через
–
столбцы матрицы А,
– столбец неизвестных. Тогда произведение
матрицы А на столбец Х можно представить
в виде:
–
линейная оболочка, натянутая на столбцы
матрицы А.
Следовательно, образ этого линейного отображения есть линейная оболочка, натянутая на столбцы матрицы А:
.
Замечание. Обычно
линейное отображение
обозначают не буквой
,
а той же буквой, что и матрицу, с помощью
которой определяется это отображение:
,
где
,
т.е.
это отображение, которое каждому столбцу
ставит в соответствие столбец
,
так что
.
Обычно столбец
обозначают буквой
,
т.е.
.
И вместо того, чтобы говорить о ядре и
образе линейного отображения
,
говорят: ядро матрицы А, образ матрицы
А, молчаливо подразумевая под этим ядро
и образ соответствующего линейного
отображения.
(Заметим, в скобках, что вот такие "молчаливые подразумения", о которых не пишут, и, даже не говорят, полагая их очевидными, составляют одну из трудностей при изучении математики. Сами же математики признают, что, бывает, две пропущенные подряд "очевидности" составляют почти непреодолимую трудность.)
Пример
4. Пусть
– отображение, которое каждому вектору
пространства V ставит в
соответствие столбец его координат,
относительно некоторого фиксированного
базиса пространства V.
Очевидно, что ядро этого отображения
нулевое, т.е. состоит из одного нулевого
вектора, а образ этого отображения
совпадает с пространством столбцов
:
.
Пример
5. Легко видеть, что
,
.
Теорема.
Пусть
линейное отображение векторных
пространств. Тогда ядро линейного
отображения
является векторным подпространством
пространства
,
а образ
– векторным подпространством пространства
.
Доказательство.
1) Пусть
,
.
Тогда
.
Но f – гомоморфизм,
поэтому,
,
.
2)
.
Так как f – гомоморфизм,
то
,
,
.
Теорема доказана.
Теорема
(О размерности ядра и образа линейного
отображения.) Пусть
линейное отображение векторных
пространств. Тогда
.
Доказательство.
Пусть
и
– базис ядра. Так как
– подпространство пространства V,
то дополним базис ядра до базиса
пространства V. Пусть
– базис пространства V и
.
Докажем, что
– базис
,
откуда сразу же будет следовать теорема.
Докажем, что
является порождающей системой
подпространства
.
Пусть
– произвольный вектор подпространства
.
Тогда
.
Разложим вектор х по базису
пространства V:
,
где
.
Отсюда,
,
ч.т.д.
Здесь, мы
воспользовались свойством линейности
гомоморфизма f и тем, что
,
откуда
.
Докажем, что
является линейно независимой системой.
Пусть
.
По свойствам линейности,
.
Разложим
вектор v по базису ядра:
,
откуда получаем равенство:
.
Так
как
– базис пространства V,
то все коэффициенты в этой линейной
комбинации равны нулю, т.е. система
может представлять нулевой вектор
только тривиально и она является линейно
независимой, ч.т.д.
Теорема доказана.
п.5. Матрица линейного отображения.
Пусть
– линейное отображение векторного
пространства V в векторное
пространство W над полем
K,
–
базис пространства V,
–
базис пространства
W,
– произвольный вектор,
– его образ в пространстве W.
Поставим задачу нахождения вектора f(x) для заданного вектора х.
Разложим вектор х по данному базису:
.
Здесь
– координаты вектора х относительно
базиса
пространства V. Так как f
– линейное отображение, то
.
(1)
Из
этого равенства мы видим, что если мы
знаем образы базисных векторов
,
то тем самым мы найдем образ f(x)
любого вектора х из пространства V.
Разложим образы
базисных векторов
,
по базису
пространства W:
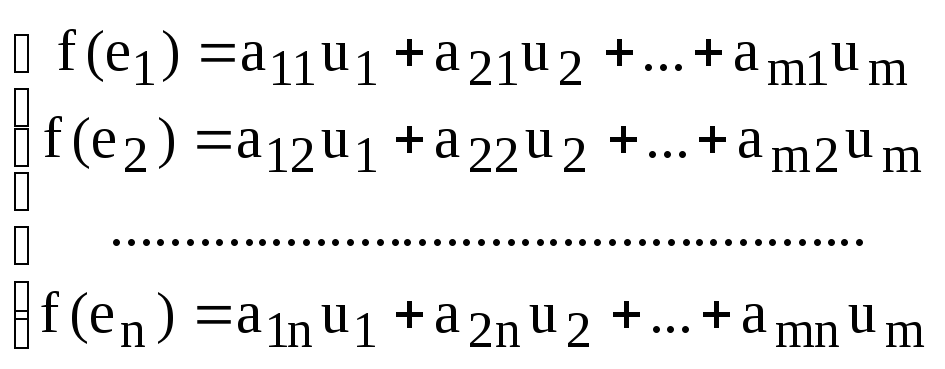(2)
Определение. Матрица
,
взятая
из равенств (2), называется матрицей
линейного отображения
относительно базисов
и
пространств V и W
соответственно.
Замечание. Равенства (2) удобно записывать в матричной форме:
(3)
Здесь,
при умножении строки
на матрицу А по правилам умножения
матриц, получаем строку длины n,
так что равенство (3) есть равенство двух
строк одинаковой длины, которое мы
рассматриваем как равенство матриц.
Две строки равной длины равны, если
равны ее соответствующие компоненты.
Приравнивая соответствующие компоненты,
получаем равенства (2).
Обозначение.
Удобно снабжать матрицу линейного
отображения двумя нижними индексами:
.
Теперь равенство (3) можно записать в виде:
.
(4)
Равенство (1) тоже можно записать в матричной форме:
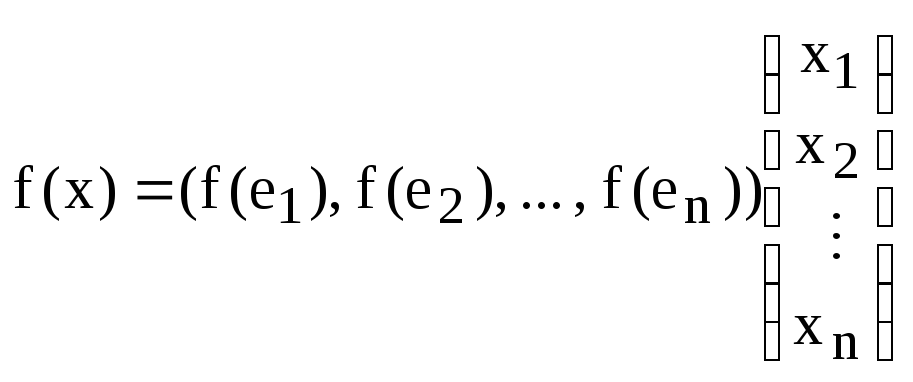(5)
Теперь, подставим равенства (2) в равенство (1). Но выполним эту подстановку в матричной форме, т.е. подставим равенство (4) в равенство (5). Получаем:
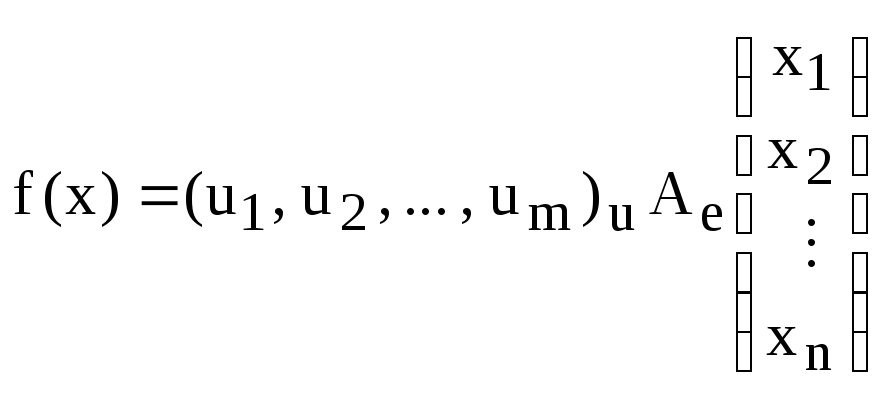(6)
Обозначим
.
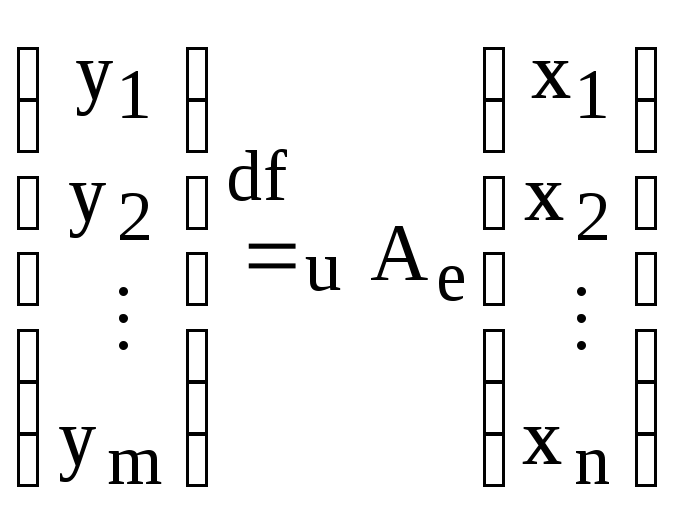Тогда,
,
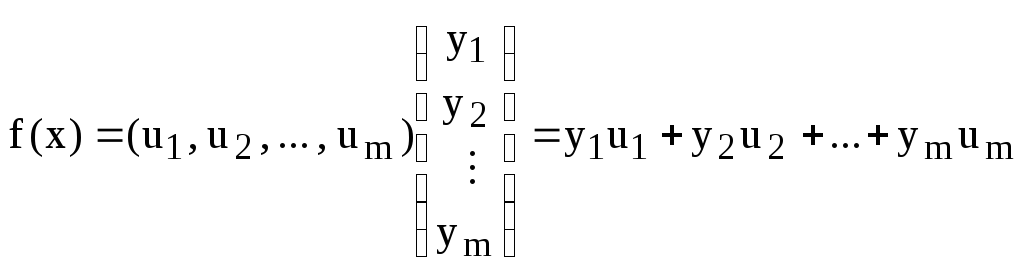где
–
координаты вектора
относительно базиса
.
Таким образом, мы
выполнили поставленную задачу нахождения
координат вектора
и тем самым доказали следующую теорему.
Теорема.
Пусть
– линейное отображение векторных
пространств,
и
– базисы
и
соответственно.
Пусть
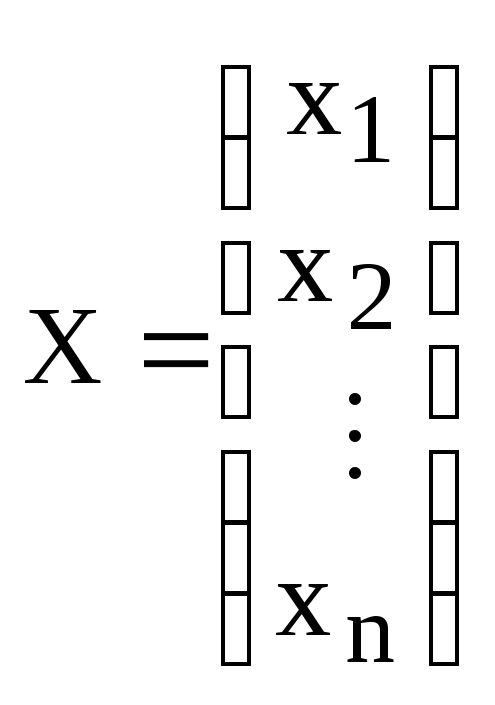– координаты вектора
,
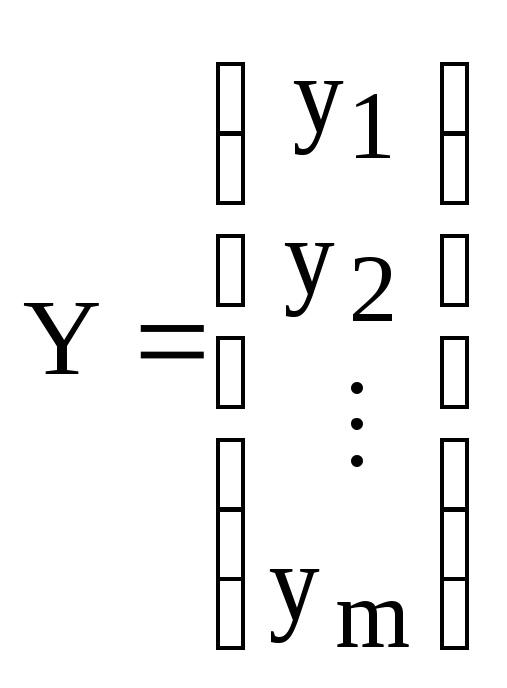– координаты вектора
.
Тогда
,
(7)
где А – матрица данного линейного отображения.
п.6. Матрица линейного оператора.
Определение.
Пусть
– линейный оператор (эндоморфизм),
действующий на пространстве V
над полем K. Пусть
–
базис пространства V,
– произвольный вектор,
– его образ в пространстве V.
Разложим вектор х по данному базису:
,
где
– координаты вектора х относительно
базиса
пространства V. Так как f
– линейное отображение, то
.
Разложим образы
базисных векторов
,
,
по базису
пространства V :
.
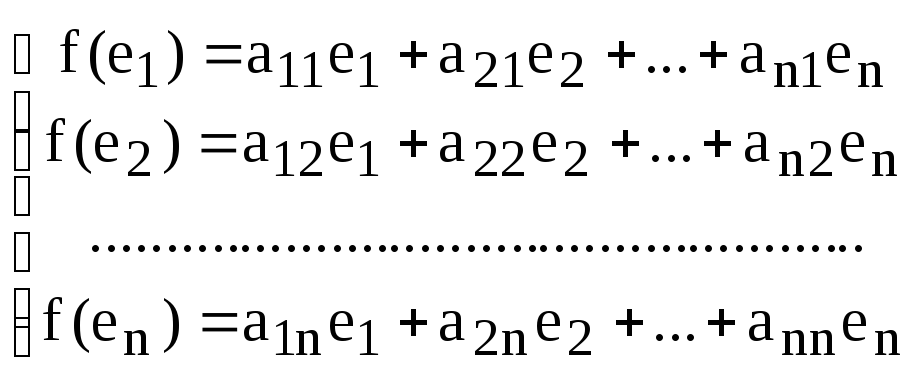(8)
Определение. Матрица
,
называется
матрицей линейного оператора
относительно базиса
пространства V.
Равенства (8) в матричной форме:
.
(9)
Аналогично предыдущей доказывается теорема.
Теорема.
Пусть
– линейный оператор,
– базис V.
Пусть
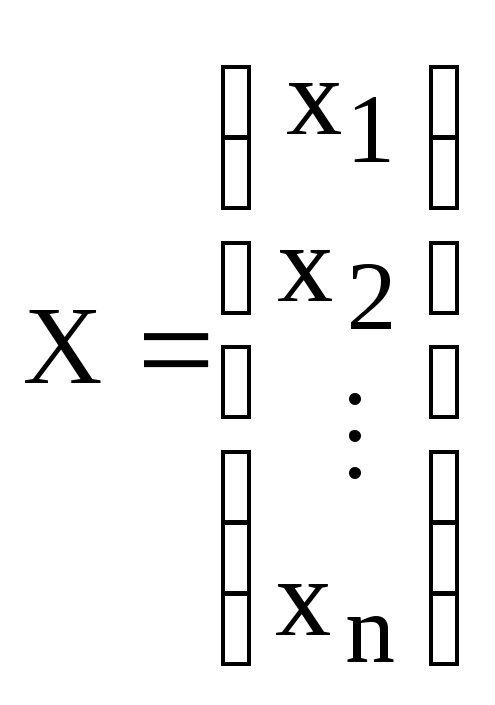– координаты вектора
,
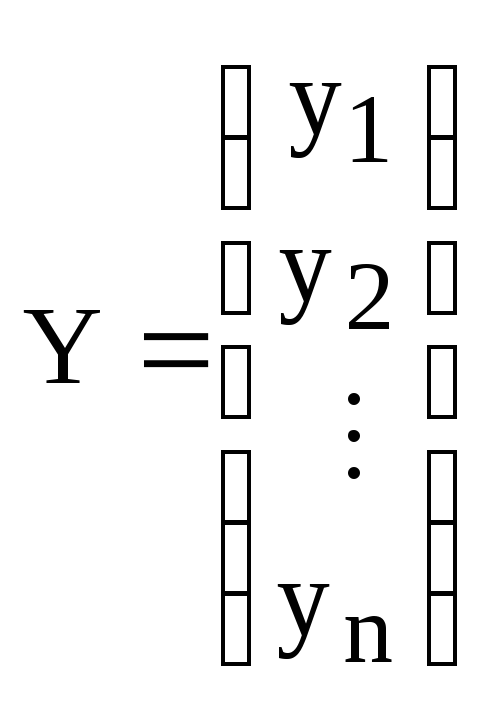– координаты вектора
.
Тогда
,
(10)
где А – матрица данного линейного оператора.
п.7. Изменение матрицы линейного отображения и линейного оператора при изменении базиса.
Теорема.
Пусть V, W –
векторные пространства над полем K,
,
– два базиса пространства
,
,
– два базиса пространства
.
Пусть С – матрица перехода от базиса
к базису
,
–
матрица перехода от базиса
к базису
.
Пусть А – матрица линейного отображения
,
относительно базисов
и
,
– матрица этого же линейного отображения
относительно базисов
и
.