golovizin_lekcii_po_lineynoy_algebre_2_semestr / Лекция 21. Обратная матрица

4

Лекции по алгебре и геометрии. Семестр 2.

Лекция 21. Обратная матрица.

Краткое содержание: вычисление определителей, миноры и алгебраические дополнения, разложение определителя по элементам строки (столбца), свойство ортогональности, формула обратной матрицы.

п.1. Вычисление определителей.

Определение. Квадратная матрица называется треугольной, если все ее элементы стоящие выше или ниже главной диагонали равны нулю:

.

Теорема. Определитель треугольной матрицы равен произведению элементов стоящих на главной диагонали:

.

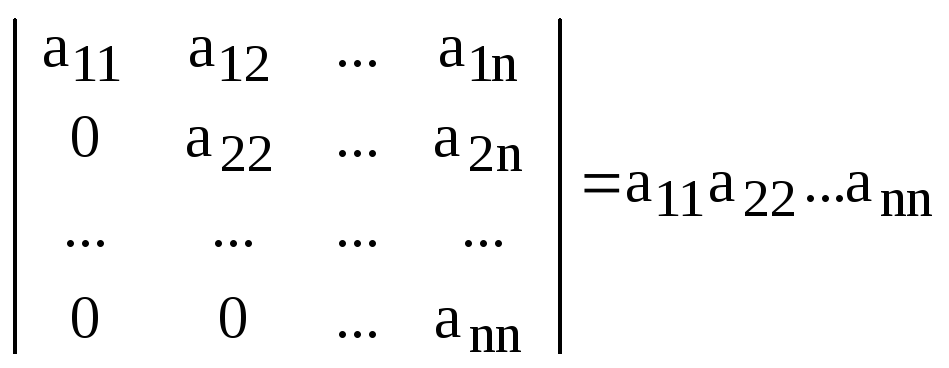Доказательство. Любой член определителя представляет собой, по определению, произведение элементов матрицы, взятых в точности по одному из каждой строки и каждого столбца. Из первого столбца можно взять лишь элемент , т.к. остальные равны нулю. Из второго столбца можно взять лишь , т.к. из первой строки элемент уже взят, а остальные равны нулю. И т.д. мы видим, что в алгебраической сумме членов определителя, лишь один член определителя не равен нулю и

.

Теорема доказана.

Следствие. Определитель диагональной матрицы равен произведению элементов стоящих на главной диагонали:

.

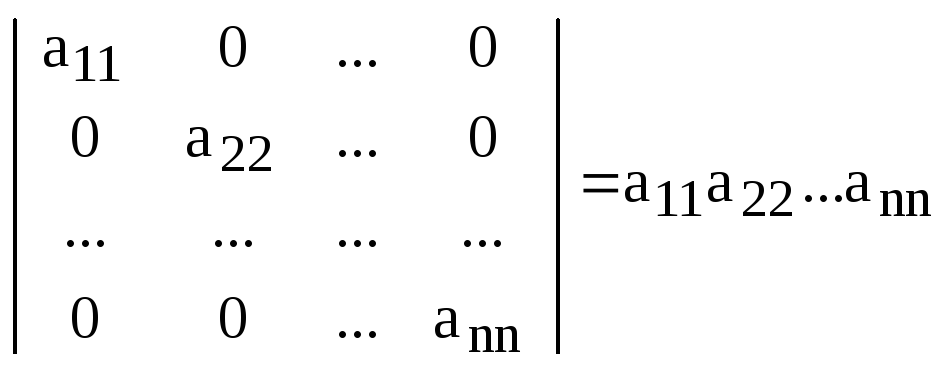Один из способов вычисления определителя, заключается в том, чтобы используя его сваойства привести определитель к треугольному виду. Продемонстрируем этот способ на примере.

Пример. Вычислить определитель .

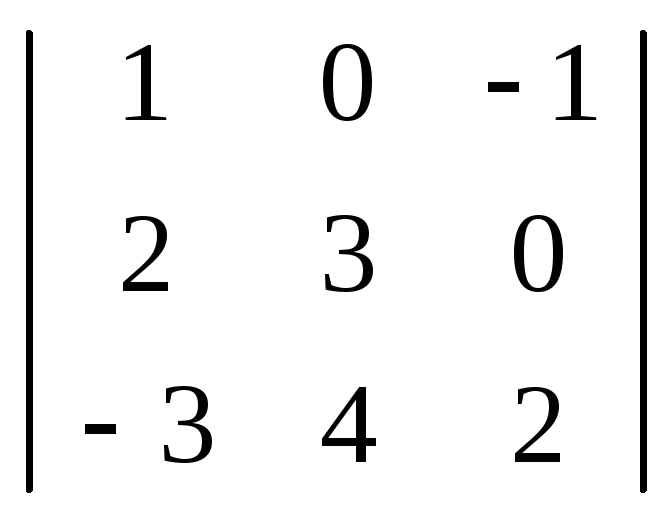Решение. По теореме о свойствах определителя определитель не изменит своего значения, если к строке (столбцу) прибавить другой столбец (другую строку), умноженный на како-либо число. Используем это свойство.

1) Умножим первую строку на (– 2) и прибавим ко второй строке:

.

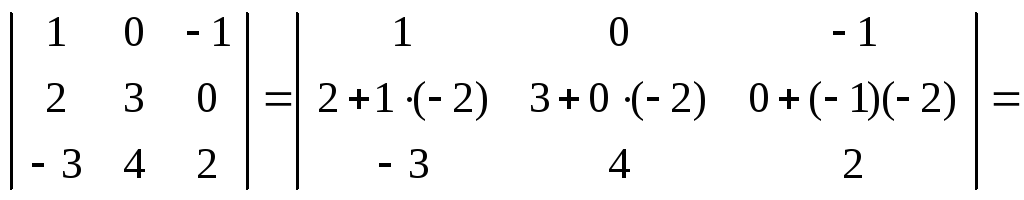
2) Умножим первую строку на 3 и прибавим к третьей:

.

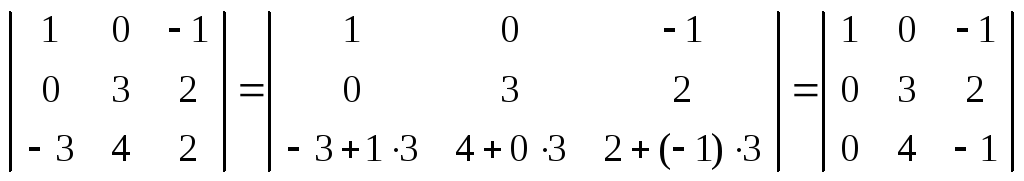3) Умножим третий столбец на 4 и прибавим ко второму:

.

Ответ: – 11.

п.2. Миноры и алгебраические дополнения.

Определение. Минором элемента определителя – го порядка называют определитель – го порядка, который получается из данного определителя вычеркиванием - й строки и – го столбца, на пересечении которых стоит элемент .

Обозначение: .

Определение. Алгебраическим дополнением элемента определителя – го порядка называют его минор, взятый со знаком плюс, если – четное число и со знаком минус в противном случае.

Обозначение: .

Пример. В определителе 3 – го порядка

.

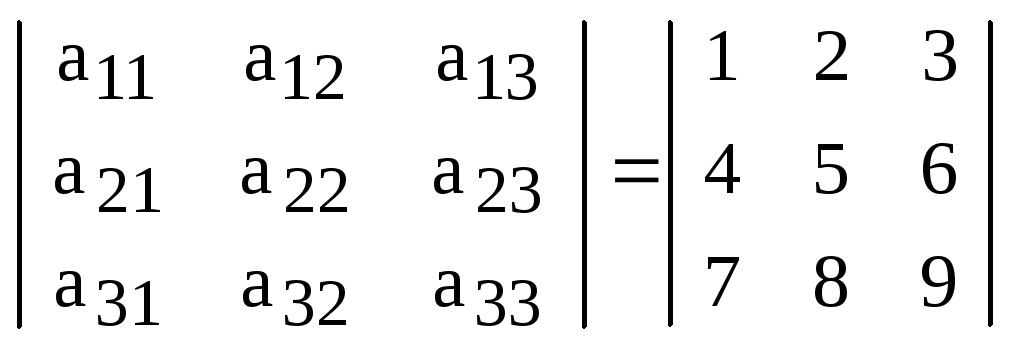найти все миноры и алгебраические дополнения элементов второго столбца.

Решение.

, ,

, ,

, .

Ответ:

, .

п.2. Разложение определителя и свойство ортогональности.

Теорема. (О разложении определителя.)

Определитель равен сумме произведений элементов любой строки (или любого столбца) определителя на их алгебраические дополнения:

, ; (1)

или

, . (2)

Доказательство. В силу равноправия строк и столбцов достаточно доказать теорему для столбцов. Для простоты записи, докажем формулу разложения по элементам первого столбца:

.

Доказательство формулы разложения определителя по элементам произвольного столбца проводится аналогично.

Используя правила действий с матрицами и, в частности, со столбцами мы можем расписать столбец в виде:

.

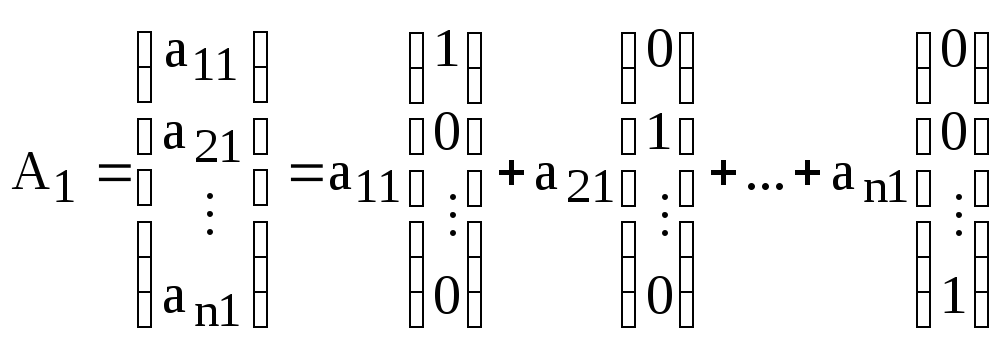Обозначим

, , …, .

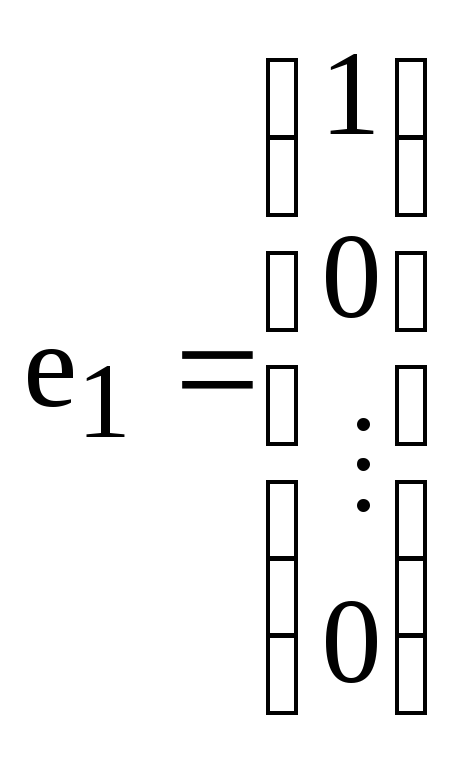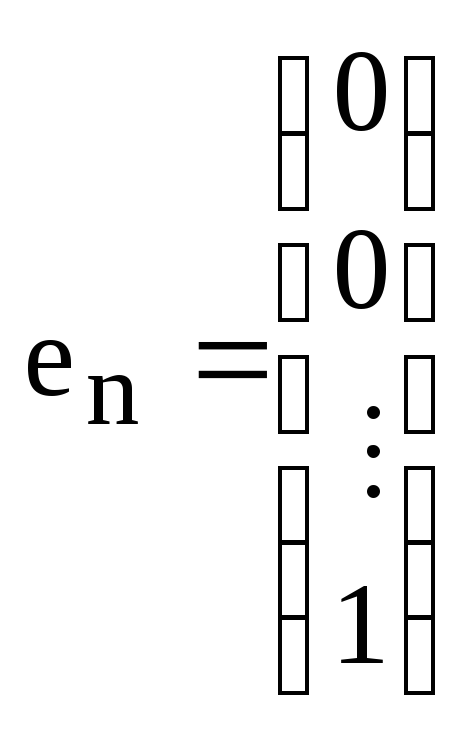Тогда

и, используя свойство линейности, получаем:

.

Вычисляем все определители, стоящие в правой части последнего равенства.

.

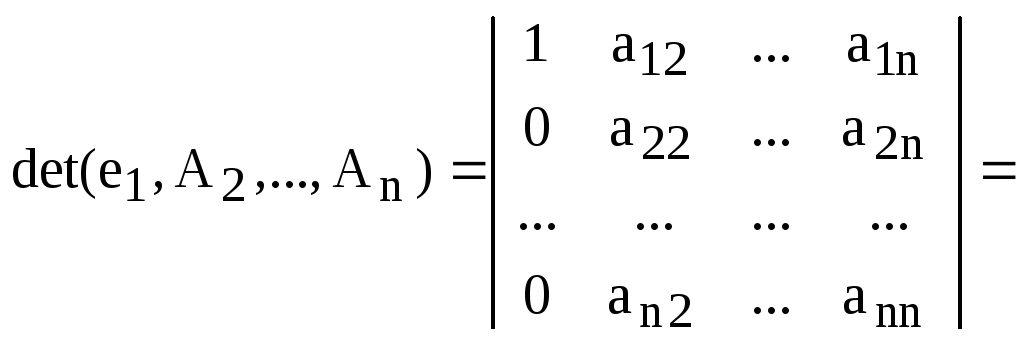
Заметим, что все члены определителя содержащие элемент из первой строки, но не из первого столбца равны нулю. Действительно, если , то из первого столбца в произведении должен стоять элемент не из первой строки, т.е. нуль. Таким образом, в сумме остаются члены определителя с превым множителем , .

Далее, очевидно, что и суммирование в сумме оставшихся членов определителя ведется по всем перестановкам множества (2, …, n), т.е.

.

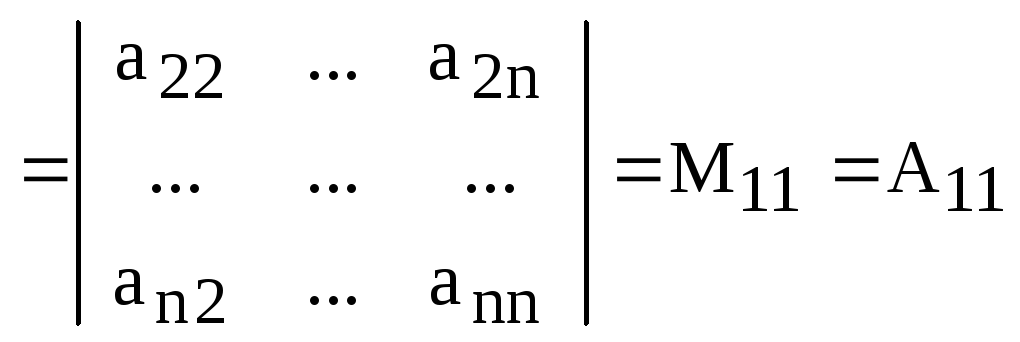Далее, в следующем определителе переставим первую и вторую строки. Тогда по только что доказанному, получаем:

. Следующие определители вычисляются аналогично.

Теорема доказана.

Замечание. Формула (1) называется разложением определителя по элементам – й строки, (2) – разложением определителя по элементам – го столбца.

Формулы (1) и (2) можно записать в матричной форме:

; .

Замечание. Разложение определителя но элементам строки (столбца) применяют для вычисления определителей небольшого порядка (третьего или максимум четвертого порядка) или определителей более высокого порядка, но с большим количеством нулевых элементов.

Пример.

.

Комментарии к примеру: сначала мы разложили определитель по элементам первого столбца, затем получившийся определитель 3 – го порядка разложили по элементам 1 – й строки и в конце вычислили определитель 2 – го порядка.

Замечание. Понятно, что при разложении определителя по элементам строки или столбца нужно выбирать строку или с столбец с наибольшим количеством нулей.

Теорема. (свойство ортогональности строк и столбцов определителя.)

Сумма произведений элементов любой строки (столбца) определителя на алгебраические дополнения соответсвующих элементов другой строки (столбца) определителя равна нулю:

, (3)

и

, . (4)

Доказательство. В силу равноправия строк и столбцов определителя достаточно доказать (4).

Рассмотрим определитель:

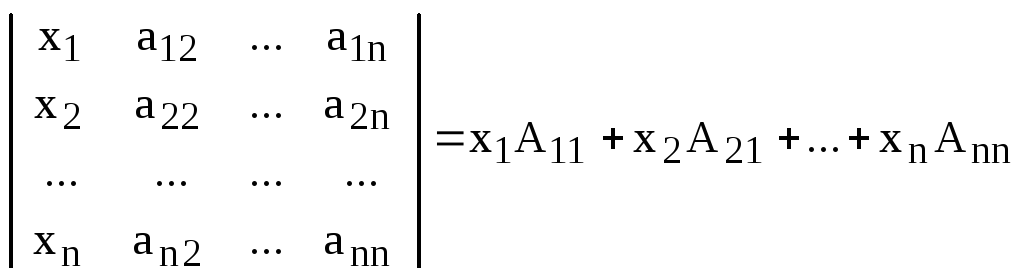. (5)

Этот определитель разложен здесь по элементам первого столбца. Равенство (5) верно для любых значений переменных . Подставляя вместо них соответствующие элементы j-го столбца, в левой части равенства (5) получаем нуль, так как получившийся определитель имеет два равных столбца:

.

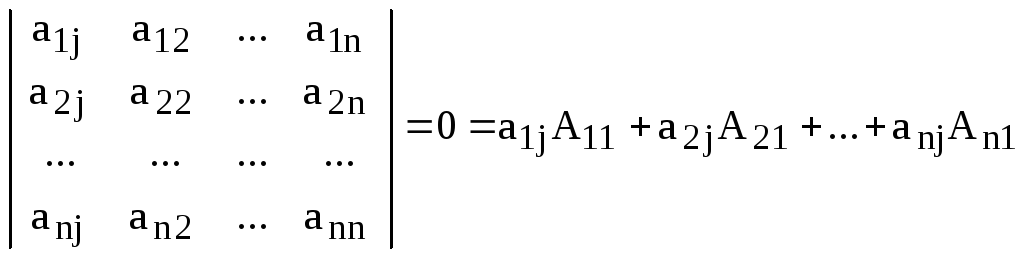Мы доказали (4) для . Аналогично доказывается и общий случай.

Теорема доказана.

Формулы (3) и (4) можно записать в матричной форме:

; (3)

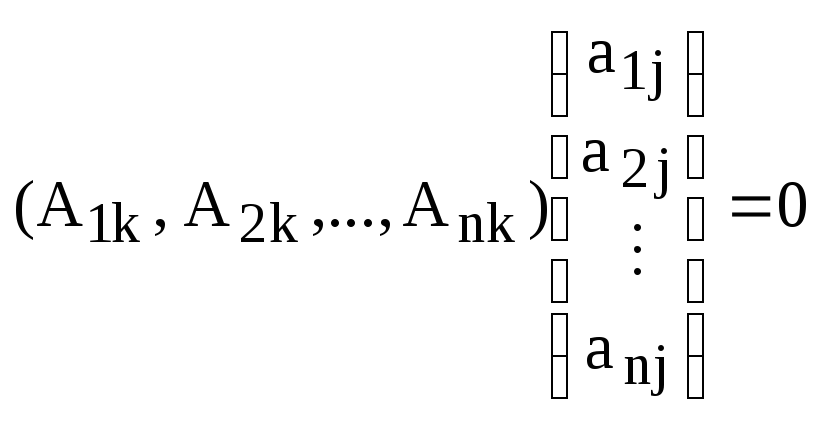, (4)

где .

Обе теоремы можно записать в виде одной.

Теорема (Свойство ортогональности определителя).

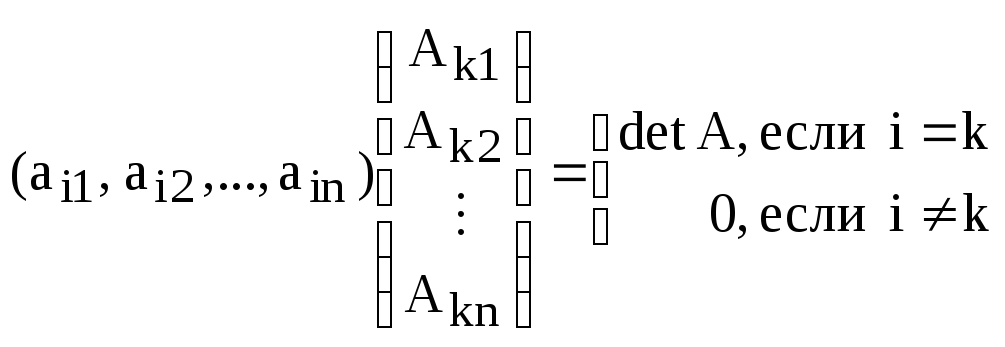; (6)

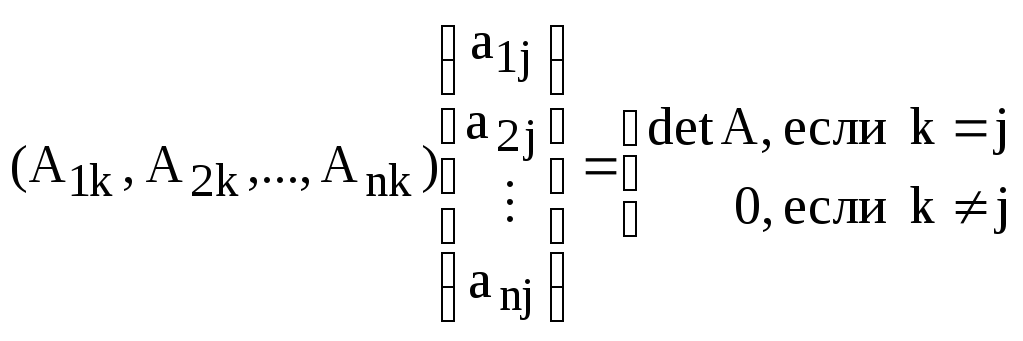. (7)

п.3. Союзная матрица.

Пусть дана квадратная матрица – го порядка. Для каждого ее элемента найдем его алгебраическое дополнение и составим матрицу

, в которой вместо элемента стоит его алгебраическое дополнение .

Затем полученную матрицу транспонируем: .

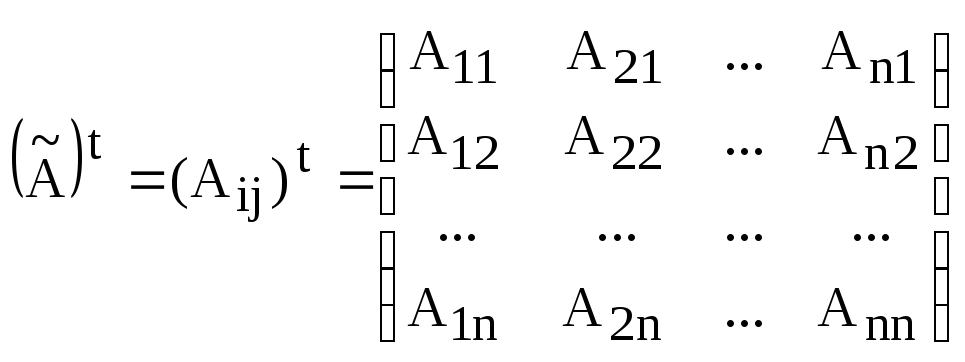Определение. Матрица называется союзной (взаимной, присоединенной).

Обозначение. Союзную матрицу часто обозначают А*. Таким образом, .

Следующее утверждение носит вспомогательный характер и мы принимаем его без доказательства.

Лемма. Определитель произведения квадратных матриц равен произведению их определителей.

.

Теорема. (Необходимые и достаточные условия существования обратной матрицы.)

1. Для того, чтобы квадратная матрица была обратимой необходимо и достаточно, чтобы ее определитель был не равен нулю.

2. Обратная матрица может быть найдена по формуле:

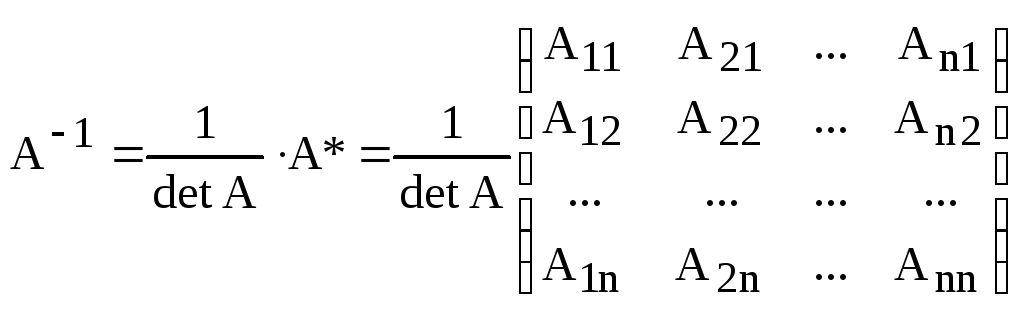. (8)

Доказательство. 1) Пусть А обратимая матрица, т.е. существует обратная к ней . Тогда

.

С одной стороны, в силу леммы,

,

а с другой стороны,

.

Получаем,

,

откуда и следует, что .

В частности, из последнего равенства следует, что

.

2) Пусть .

Из формул (6) и (7) предыдущей теоремы сразу же следует матричное равенство: .

Или в развернутом виде:

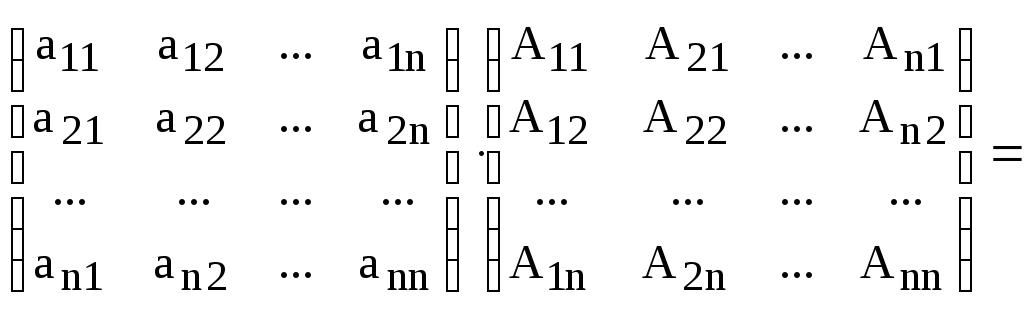
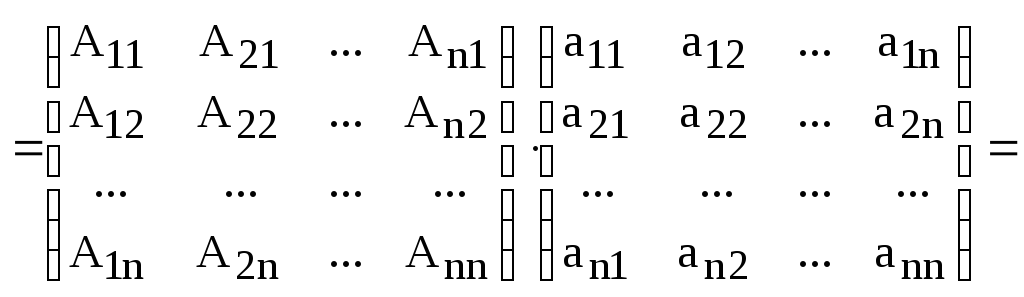
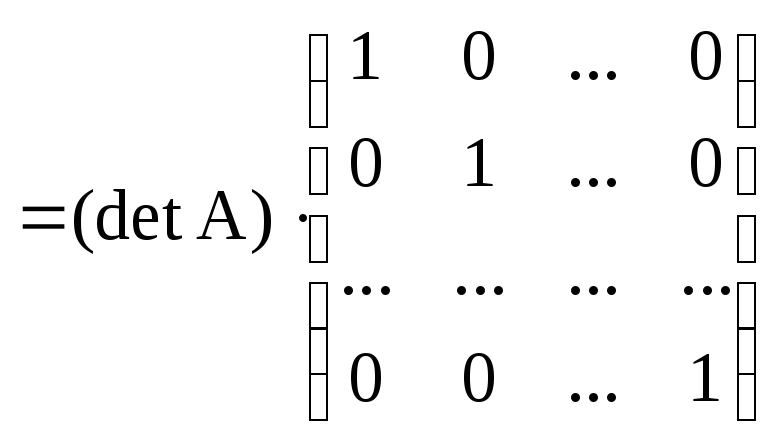, откуда и следует (8).

Теорема доказана.