golovizin_lekcii_po_lineynoy_algebre_2_semestr / Лекция 19. Алгебра матриц

Лекции по алгебре и геометрии. Семестр 2.

Лекция 19. Алгебра матриц.

Краткое содержание: Основные определения, действия с матрицами и их свойства, нулевая и единичная матрицы, обратная матрица и ее свойства, обратимые матрицы.

Глава 1. Алгебра матриц.

п.1. Основные определения.

Пусть К – поле. Элементы поля К мы будем называть скалярами. Под полем К можно понимать или поле действительных чисел или поле комплексных чисел.

Определение. Матрицей размера над полем К называется таблица элементов поля К, имеющую строк и столбцов.

Обозначение:

.

Определение. Элементы называются элементами матрицы, где i – номер строки, в которой находится элемент , j – номер столбца.

Определение. Матрица размеров :

называется строкой длины .

Определение. Матрица размеров :

называется столбцом высоты .

Определение. Матрица размеров называется квадратной матрицей – го порядка.

Определение. Матрица, все элементы которой равны нулю, называется нулевой.

В квадратной матрице выделяют две диагонали, как диагонали квадрата: главную диагональ и побочную диагональ.

Главную диагональ образуют элементы , т.е. элементы с одинаковыми нижними индексами.

Побочную диагональ образуют элементы .

Определение. Квадратная матрица, в которой все элементы вне главной диагонали равны 0, называется диагональной:

.

Определение. Матрица В размера называется транспонированной по отношению к матрице А размера , если к – й столбец матрицы В состоит из элементов к – й строки матрицы А, для всех .

Обозначение: .

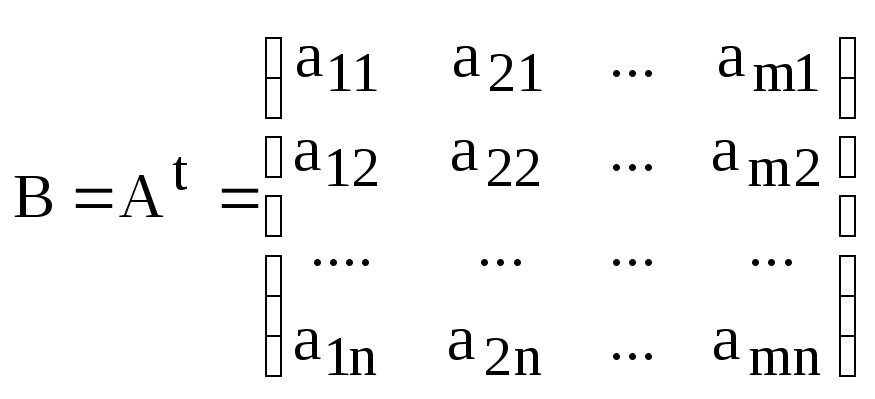Определение. Процесс (процедура) получения транспонированной матрицы из данной называется транспонированием матрицы.

Пример:

, .

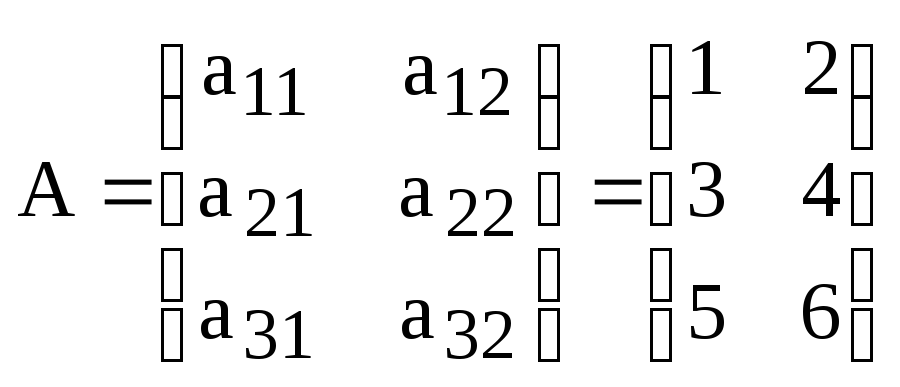Определение. Две матрицы и называются равными, если они имеют одинаковые размеры и для всех значений индексов выполняется равенство .

п.2. Сложение матриц.

Определение. Суммой матриц и одинаковой размерности называется третья матрица такой же размерности , где ее элементы определяются равенством для всех значений индексов.

Обозначение: .

Другими словами, для того, чтобы найти сумму двух матриц одинаковой размерности, нужно сложить соответствующие элементы (т.е. элементы, имеющие одинаковые нижние индексы) этих матриц.

Замечание. Сложение матриц различных размеров не определено. (Их нельзя складывать!)

Пример: , ,

.

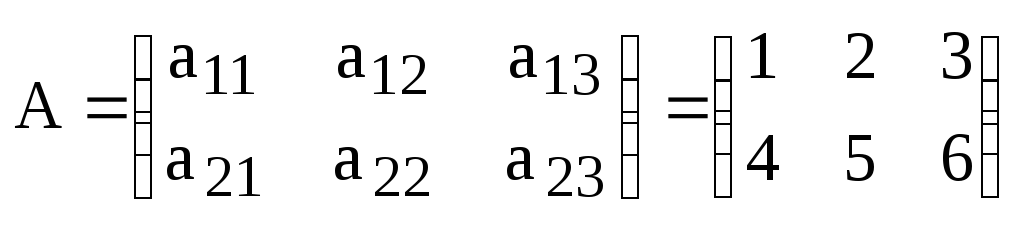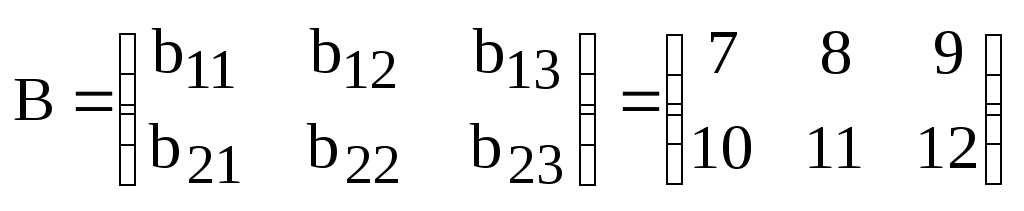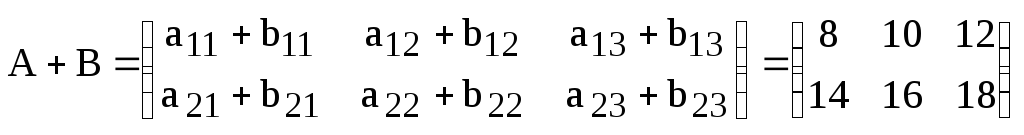Определение. Матрица В называется противоположной матрице А, если она удовлетворяет равенству , где 0 – нулевая матрица.

Обозначение: .

Множество всех матриц размера над полем K обозначим через

Теорема. (Свойства сложения матриц.)

Множество относительно сложения является абелевой группой.

Другими словами, сложение матриц подчиняется следующим законам:

1) ассоциативность: справедливо равенство ;

2) существование нулевой матрицы:

– нулевая матрица, такая, что верны равенства ;

3) существование противоположной матрицы:

, : ;

4) коммутативность:

.

п.3. Умножение матрицы на скаляр.

Определение. Произведением скаляра на матрицу называется матрица тех же размеров, что и матрица А, где элементы определяются равенством , для всех значений индексов.

Обозначение: .

Другими словами, для того, чтобы умножить матрицу на скаляр, нужно каждый элемент матрицы умножить на данный скаляр.

Пример:

,

.

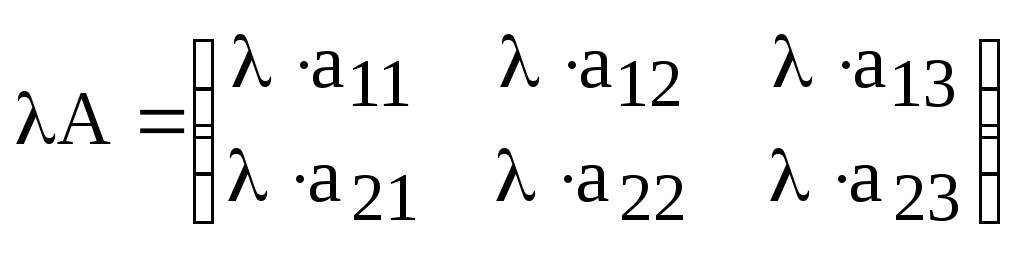Замечание. Легко видеть, что умножив матрицу на (–1) мы получаем противоположную матрицу: .

Теорема. (Свойства умножения матрицы на скаляр.)

Умножение матрицы на скаляр подчиняется законам:

5) ассоциативность: и

;

6) если 1 – единица поля K, тогда

;

7) дистрибутивность умножения относительно сложения скаляров: и

;

8) Дистрибутивность умножения относительно сложения матриц: и

.

Следствие. Множество относительно сложения матриц и умножения матриц на скаляр является векторным пространством над полем К.

Обозначим через множество всех столбцов высоты n с элементами из поля K.

Следствие. Множество является векторным пространством над полем K.

Определение. Векторное пространство называется арифметическим векторным пространством столбцов высоты n.

п.4. Умножение матриц.

Определение. Произведением строки длины n на столбец высоты n называется скаляр, вычисляемый по правилу:

.

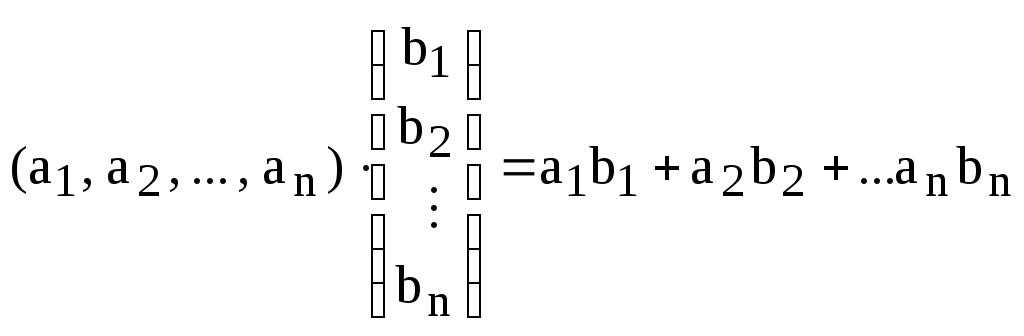Замечание. Из определения следует, что для умножения строки на столбец необходимо, чтобы длина строки была равна высоте столбца. В противном случае произведение строки на столбец не определено.

Пример.

Определение. Произведением матрицы размера на матрицу размера называют матрицу размера , где элемент является результатом произведения – й строки матрицы А на – й столбец матрицы В для всех значений индексов , , т.е.

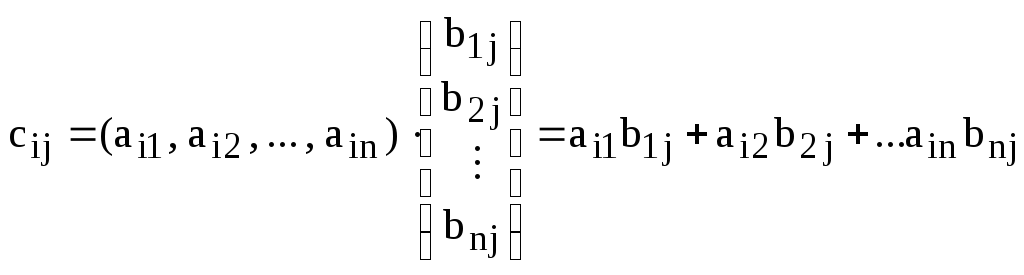
или

.

Обозначение: .

Другими словами, чтобы умножить две матрицы, нужно каждую строку первой матрицы умножить на каждый столбец второй матрицы. Умножая первую строку первой матрицы на каждый столбец второй матрицы мы получим все элементы первой строки матрицы произведения, затем делаем то же самое для второй строки первой матрицы и т.д.

Замечание. Из определения следует, что умножение матриц возможно только тогда, когда ширина первой матрицы (т.е. число ее столбцов) равна высоте второй (т.е. числу ее строк)

Пример.

.

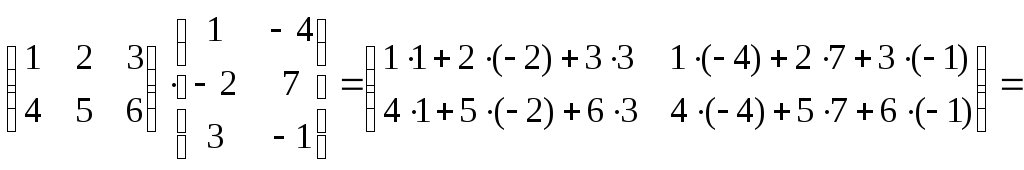
Определение. Квадратную матрицу – го порядка называют единичной матрицей n-го порядка и обозначают буквой Е, если для любой квадратной матрицы А – го порядка справедливо равенство: .

Множество всех квадратных матриц n-го порядка будем обозначать через .

Теорема. Множество содержит единичную матрицу n-го порядка, которой является матрица

.

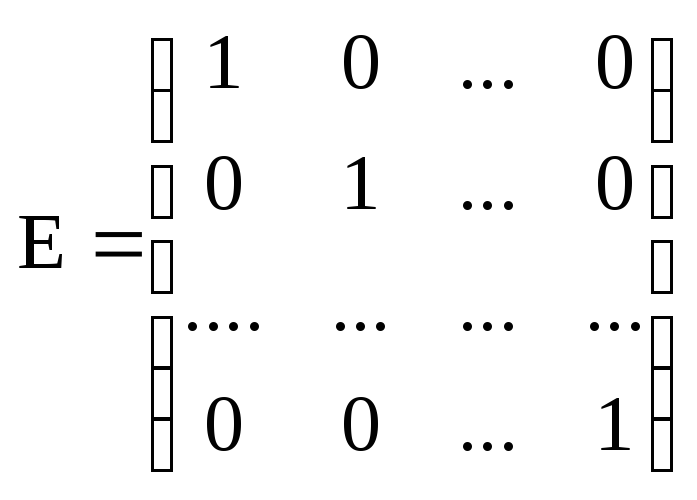Доказательство этой теоремы предоставляется читателю.

Теорема. Единичная матрица Е является единственной в множестве .

Доказательство. Пусть еще одна единичная матрица. Тогда, по определению, . Положим , тогда . Далее, по определению, . Положим здесь . Получаем равенство, отсюда имеем , ч.т.д.

Заметим, что точно также доказывается единственность нейтрального элемента (при условии его существования) в любой алгебраической структуре.

Теорема доказана.

Из теоремы следует, что никакая другая матрица, кроме матрицы 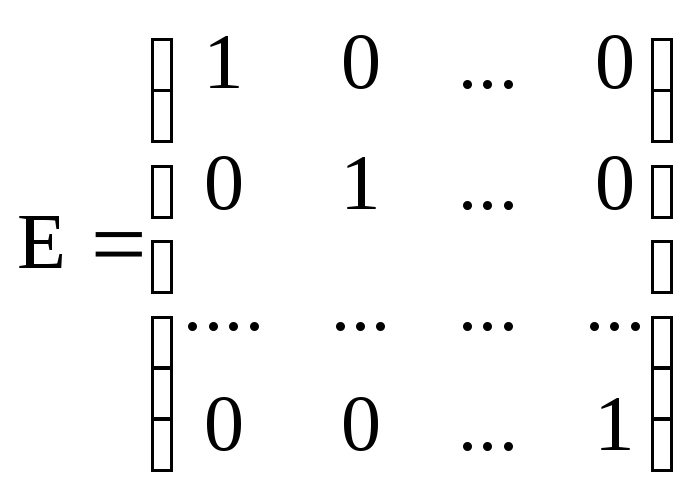не является единичной.

Теорема. (Свойства умножения матриц.)

Умножение матриц подчиняется следующим законам:

9) ассоциативность:

;

10) существование единичной матрицы:

: ;

дистрибутивность умножения относительно сложения матриц:

11) дистрибутивность умножения относительно сложения матриц:

и

12) умножение матриц связано с умножением матрицы на число естественным законом: и верно равенство:

.

Замечание. Для квадратных матриц одного порядка выполняются все 12 свойств. Это говорит о том, что множество всех квадратных матриц одного и того же порядка образует алгебру матриц над полем К.

Замечание. Умножение матриц не обладает свойством коммутативности. Для доказательства достаточно привести один контрпример.

Пусть , . Тогда , .

Аналогичный пример можно привести для квадратных матриц любого порядка.

Последнее равенство говорит о том, что квадратные матрицы имеют делители нуля.

Следствие. Множество всех квадратных матриц n-го порядка над полем K является некоммутативным кольцом с единицей и с делителями нуля.

Доказательство. На множестве всех квадратных матриц n-го порядка над полем K определены две операции: сложение матриц и их умножение, которые подчиняются законам 1) – 4) и 9) – 11), откуда и следует, по определению, что является кольцом с единицей (см. лекцию 1, п.14 и п.15). Пример, приведенный перед формулировкой данного следствия, показывает, что кольцо имеет делители нуля.

Следствие доказано.

Определение. Натуральной степенью квадратной матрицы А называется матрица .

Нулевую степень квадратной матрицы А – го порядка по определению полагают равной единичной матрице того же порядка: .

п.5. Обратная матрица.

Определение. Матрица В называется обратной по отношению к матрице А, если

.

Из определения следует, что если матрица А имеет обратную, то обе они должны быть квадратными матрицами одного порядка.

Из определения следует, что если матрица В является обратной по отношению к матрице А, то и матрица А является обратной по отношению к матрице А.

Определение. Матрица имеющая обратную матрицу называется обратимой.

Теорема. Если квадратная матрица А имеет обратную, то она единственная.

Доказательство. Пусть В и С – две матрицы обратные к матрице А. Тогда и . Имеем,

, ч.т.д.

Теорема доказана.

Заметим, что точно также доказывается единственность симметричного элемента в любой полугруппе при условии его существования.

Обозначение: если матрица А обратимая, то обратная к ней обозначается (мы можем это сделать в силу ее единственности) через .

Заметим, что если матрица А обратимая, то обратная к ней матрица также является обратимой.

Обозначение. Множество всех обратимых матриц n-го порядка над полем K обозначается через

.

Теорема. (Свойства обратных матриц.)

1. Произведение обратимых матриц одного и того же порядка является обратимой матрицей:

, и .

2. Единичная матрица является обратимой, т.е. если Е – единичная матрица n-го порядка, то

и .

3. Если А обратимая, то и также является обратимой, т.е. если , то и .

Доказательство. 1) Пусть А и В – обратимые матрицы и , – обратные к ним. Покажем, что произведение является матрицей обратной к произведению :

.

Аналогично получаем . Следовательно, матрица АВ имеет обратную и . Отсюда следует, что матрица АВ является обратимой, т.е. , ч.т.д.

2) Так как , то по определению, , т.е. единичная матрица имеет обратную и, следовательно, единичная матрица является обратимой и .

3) Действительно, из определения следует, что матрица А является обратной по отношению к матрице , следовательно, матрица обратимая и . Более того, в силу единственности обратной матрицы следует, что

.

Теорема доказана.

Следствие. Множество является некоммутативной группой относительно умножения.

Доказательство. На множестве умножение матриц является внутренней бинарной алгебраической операцией, поэтому осталось лишь проверить аксиомы группы.

1) Ассоциативность умножения в множестве выполняется потому что умножение квадратных матриц ассоциативно (см теорему о свойствах умножения матриц).

Далее, в предыдущей теореме доказано, что:

2) единичная матрица ;

3) существует обратная ей .

Следствие доказано.

Определение. Обратимая квадратная матрица называется также неособой или невырожденной. Если квадратная матрица не имеет обратной, то она называется особой или вырожденной.

Замечание. Легко доказать существование особых матриц. Например, матрица

является особой (вырожденной, необратимой). Действительно, если бы она была обратимой, то существовала бы обратная к ней и . Пусть далее, . Тогда и отсюда получаем

или , т.е. получаем противоречие.

Аналогично, легко показать существование особых матриц любого порядка. Отсюда следует вывод, что не все квадратные матрицы являются обратимыми.

В дальнейшем, мы найдем необходимое и достаточное условие обратимости квадратной матрицы любого порядка и не только докажем существование обратимых матриц, отличных от единичной матрицы, но и выведем формулу для ее вычисления.