
- •Классификация элементов.
- •3. Элементы, рассеивающие энергию. Резисторы.
- •4. Двухполюсник индуктивного типа.
- •5. Емкость.
- •6. Взаимная индуктивность.
- •Соотношение для идеального трансформатора.
- •7. Многополюсник.
- •8. Зависимые источники энергии.
- •12. Метод контурных токов.
- •15. Матрицы параметров цепей.
- •Свойства матрицы .
- •Свойства матрицы .
- •21. Метод узловых потенциалов.
- •22.Расчет цепей на синусоидальном токе.
- •23. Изображение синусоидальных величин векторами и комплексными числами.
- •25.Задача.
- •1 Способ:
- •2 Способ:
- •Важно!!!
- •27.Мощности в цепях синусоидального тока.
- •28.Балансы мощностей.
- •30. Резонанс токов (резонанс в параллельном контуре).
- •33. Классический метод расчета переходных процессов.
- •Переходные процессы.
- •34.ВключениеRLцепи на постоянное напряжение.
- •35.ВключениеRLцепи на источник синусоидального напряжения.
- •36.Задачи с некорректными начальными условиями.
- •37.Разряд конденсатора с начальным напряжением наRl-цепь.
- •1 Случай.Апериодический характер процесса.
- •38.Разряд конденсатора с начальным напряжением наRl-цепь.
- •2 Случай.Граничный характер процесса.
- •39. Разряд конденсатора с начальным напряжением на rl-цепь.
- •Периодический характер процесса.
- •2) .
- •40. Операторный метод расчета переходных процессов.
- •41.Расчет переходных процессов операторным методом.
- •Переход от изображений к оригиналам.
- •43. Общие свойства четырехполюсников.
- •48.Задача на а – параметры.
- •49.Характеристические параметры четырехполюсников.
- •50.Последовательное соединение четырехполюсников.
- •51.Параллельное соединение четырехполюсников.
- •52.Каскадное соединение четырехполюсников.
- •54,Методы расчета нелинейных элементов.
- •57.Метод Ньютона-Рафсона.
8. Зависимые источники энергии.
Источник ЭДС, управляемый напряжением:

Рассмотрим четырехполюсник, изображенный
на рисунке. Можем сказать, что
 - разрыв цепи, а
- разрыв цепи, а .
Четырехполюсники описываютсяматричными
уравнениями, поэтому, чтобы иметь
возможность моделировать зависимые
источники энергии, запишем полученные
уравнения в матричном виде:
.
Четырехполюсники описываютсяматричными
уравнениями, поэтому, чтобы иметь
возможность моделировать зависимые
источники энергии, запишем полученные
уравнения в матричном виде:
 .
.
Источник тока, управляемый напряжением:

![]() ,
, .
Это соответствует матричному уравнению:
.
Это соответствует матричному уравнению:

Источник ЭДС , управляемый током:

Ток в первой цепи должен протекать,
тогда
 (кинули закоротку),
(кинули закоротку), .
.

Источник тока, управляемый током:

Это, как раз, наш транзисторный источник
тока:
 .
Тогда:
.
Тогда:

Итак, коллекторный ток управляется током, который мы загоняем в базу транзистора. Однако не только источником тока, управляемым током, стоит какая-то физическая модель. Об этом в следующей теме.
9.
10.


11.
12.
12. Метод контурных токов.
Сначала выбираем произвольно направления токов в контурах. Так как оно будет условным, то исходя из полученного в дальнейшем знака, мы будем судить о направлении тока. Отталкиваться будем от законов Кирхгофа. Для нашего примера (см. рисунок) первый закон Кирхгофа имеет вид:
 .
.
Выбираем дерево, которое включает в
себя максимальное количество ветвей
без источников тока. Пусть это будут
ветви, содержащие
 .
Запишем второй закон Кирхгофа для
выбранных контуров:
.
Запишем второй закон Кирхгофа для
выбранных контуров:

Законы Кирхгофа дают полную систему уравнений имеющую максимальную размерность. Конкретные методы позволяют уменьшить размерность системы.
В данном случае мы возьмем токи из первого закона Кирхгофа и подставим их в уравнения из второго закона Кирхгофа. Получим:


Систему уравнений
 мы можем трактовать следующим образом.
Через каждый элемент протекает некийконтурный ток:
мы можем трактовать следующим образом.
Через каждый элемент протекает некийконтурный ток:

 .
Значит падение напряжения на элементе
обусловлено протеканием через него
всех контурных токов, причем напряжение
от собственного контурного тока всегда
берется со знаком плюс. Падения напряжений
от остальных контурных токов берутся
со знаком плюс, если направления контурных
токов совпадает с направлением
рассматриваемого тока, и в обратном
случае с минусом. Естественно, полученная
матрица сопротивлений симметрична
относительно главной диагонали.
.
Значит падение напряжения на элементе
обусловлено протеканием через него
всех контурных токов, причем напряжение
от собственного контурного тока всегда
берется со знаком плюс. Падения напряжений
от остальных контурных токов берутся
со знаком плюс, если направления контурных
токов совпадает с направлением
рассматриваемого тока, и в обратном
случае с минусом. Естественно, полученная
матрица сопротивлений симметрична
относительно главной диагонали.
13.

14.


15. Матрицы параметров цепей.
1.
Матрица сопротивлений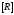 .
.
Если
цепь имеет
 ветвей, то матрица сопротивлений имеет
вид:
ветвей, то матрица сопротивлений имеет
вид:
 .
.
Строки и столбцы соответствуют номерам
ветвей цепи, на главной диагонали –
 – собственные сопротивления ветвей,
– собственные сопротивления ветвей, - взаимные сопротивления ветвей (их
обуславливает взаимная индуктивность).
Для линейных цепей
- взаимные сопротивления ветвей (их
обуславливает взаимная индуктивность).
Для линейных цепей .
На постоянном токе
.
На постоянном токе - диагональная матрица, на главной
диагонали – собственные сопротивления
ветвей:
- диагональная матрица, на главной
диагонали – собственные сопротивления
ветвей:
 .
.
Как используется матица сопротивлений; запишем закон Ома в матричной форме:
 ,
,
где
 - вектор-столбец напряжений ветвей цепи,
- вектор-столбец напряжений ветвей цепи, - вектор-столбец токов, протекающих
через ветви цепи. При нумерации ветвей
и при записи матриц и векторов всегда
должно наблюдаться соответствие, т.е.
если мы рассматриваем первую ветвь, то
- вектор-столбец токов, протекающих
через ветви цепи. При нумерации ветвей
и при записи матриц и векторов всегда
должно наблюдаться соответствие, т.е.
если мы рассматриваем первую ветвь, то должно соответствовать напряжению на
этой ветви,
должно соответствовать напряжению на
этой ветви, - ток, протекающий через эту ветвь,
- ток, протекающий через эту ветвь, - сопротивление первой ветви. Матричное
уравнение мы можем решить относительно
токов:
- сопротивление первой ветви. Матричное
уравнение мы можем решить относительно
токов:
 ,
,
где
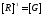 - матрица проводимостей. Для постоянного
тока
- матрица проводимостей. Для постоянного
тока

Иногда вместо
 используют обозначение
используют обозначение ,
вместо
,
вместо –
– .
Если работаем не на постоянном токе, то
нужно обращать матрицу:
.
Если работаем не на постоянном токе, то
нужно обращать матрицу:
 .
.
16.
1.Матрица «контур-ветвь»
 ;
;
Этим
матрицам абсолютно безразлично, какие
элементы находятся в ветвях, принципиальны
только параметры соединений. Запишем
алгоритм формирования матрицы
 :
:
чертится граф-схема;

выбираются условно-положительные направления ветвей (токов в ветвях);
выбирается дерево;
нумеруются ветви графа, причем сначала хорды, потом ветви дерева;
выбираются независимые контуры; мы уже говорили о том, что чтобы гарантировать независимость контура, будем замыкать контур по ветвям дерева, число независимых контуров = числу хорд;
направление контура определяется направлением образующей его хорды;
записывается матрица
 :
:

Запишем для нашего примера матрицу
 :
:



Матрицы используются потому, что при
таком представлении информация более
удобна при представлении на компьютере.
Заметим, что
 - блочная матрица:
- блочная матрица: .
Исходя из того правила, как мы формировали
матрицу
.
Исходя из того правила, как мы формировали
матрицу ,
, - всегда единичная матрица. Мы рассматриваем
независимые контура, в которые входит
только одна из хорд. Поэтому все остальные
элементы, кроме диагональных – нули.
Единичной же она будет потому, что
направление контура определяется
направлением образующей его хорды.
Получается, что матрица
- всегда единичная матрица. Мы рассматриваем
независимые контура, в которые входит
только одна из хорд. Поэтому все остальные
элементы, кроме диагональных – нули.
Единичной же она будет потому, что
направление контура определяется
направлением образующей его хорды.
Получается, что матрица - единичная, никакой информации в себе
не несет.
- единичная, никакой информации в себе
не несет.
