
- •Классификация элементов.
- •3. Элементы, рассеивающие энергию. Резисторы.
- •4. Двухполюсник индуктивного типа.
- •5. Емкость.
- •6. Взаимная индуктивность.
- •Соотношение для идеального трансформатора.
- •7. Многополюсник.
- •8. Зависимые источники энергии.
- •12. Метод контурных токов.
- •15. Матрицы параметров цепей.
- •Свойства матрицы .
- •Свойства матрицы .
- •21. Метод узловых потенциалов.
- •22.Расчет цепей на синусоидальном токе.
- •23. Изображение синусоидальных величин векторами и комплексными числами.
- •25.Задача.
- •1 Способ:
- •2 Способ:
- •Важно!!!
- •27.Мощности в цепях синусоидального тока.
- •28.Балансы мощностей.
- •30. Резонанс токов (резонанс в параллельном контуре).
- •33. Классический метод расчета переходных процессов.
- •Переходные процессы.
- •34.ВключениеRLцепи на постоянное напряжение.
- •35.ВключениеRLцепи на источник синусоидального напряжения.
- •36.Задачи с некорректными начальными условиями.
- •37.Разряд конденсатора с начальным напряжением наRl-цепь.
- •1 Случай.Апериодический характер процесса.
- •38.Разряд конденсатора с начальным напряжением наRl-цепь.
- •2 Случай.Граничный характер процесса.
- •39. Разряд конденсатора с начальным напряжением на rl-цепь.
- •Периодический характер процесса.
- •2) .
- •40. Операторный метод расчета переходных процессов.
- •41.Расчет переходных процессов операторным методом.
- •Переход от изображений к оригиналам.
- •43. Общие свойства четырехполюсников.
- •48.Задача на а – параметры.
- •49.Характеристические параметры четырехполюсников.
- •50.Последовательное соединение четырехполюсников.
- •51.Параллельное соединение четырехполюсников.
- •52.Каскадное соединение четырехполюсников.
- •54,Методы расчета нелинейных элементов.
- •57.Метод Ньютона-Рафсона.
2 Случай.Граничный характер процесса.
Данный частный случай характеризуется следующим соотношением:
 ,
,
т.е. значение подкоренного выражения в
формуле для
 равняется нулю. Но тогда
равняется нулю. Но тогда ,
и в выражениях для тока и напряжений
получаем неопределенность вида
,
и в выражениях для тока и напряжений
получаем неопределенность вида :
:
 .
.
В
этом случае принимают
 и находят предел выражения для тока при
и находят предел выражения для тока при :
:
 .
.
Теперь найдем все напряжения, исходя из полученной зависимости тока от времени:

 ,
,
где
мы учли, что
 .
Тогда напряжение на конденсаторе имеет
вид:
.
Тогда напряжение на конденсаторе имеет
вид:
 .
.
Как и для 1 случая, можно найти максимумы значений тока в контуре и напряжения на индуктивности:

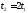 ,
,
и графики временных зависимостей токов и напряжений будут аналогичны предыдущему
39. Разряд конденсатора с начальным напряжением на rl-цепь.
В цепи нет источника, но зато содержится 2 реактивных элемента: катушка и емкость, обладающая напряжением в начальный момент времени. По второму закону Кирхгофа,



Продифференцируем уравнение по времени:

Определим ток в цепи:

Поскольку
в цепи нет источника,
 ,
тогда
,
тогда
 ,
,
где
 и
и - корни характеристического уравнения:
- корни характеристического уравнения:
 ,
,
откуда
 .
.
Запишем начальные условия:
 .
.
До
коммутации ток через индуктивность не
протекал,
 ,
с другой стороны,
,
с другой стороны,
 .
.
Нужно еще одно уравнение (цепь 2 порядка), применим 2-й закон коммутации:
 .
.
В
момент времени



 .
.
Тогда
 .
.
Решая
совместно
 и
и ,
получим:
,
получим:
 .
.
Отсюда найдем ток:




Упростим полученное выражение для
 .
Пусть
.
Пусть

 ,
,
отметим, что

Подставив это равенство в выражение
для
 ,
получим:
,
получим:
 ,
,
где
 .
.
Итак, мы рассмотрели решение данной
цепи в общем случае. Рассмотрим далее
частные случаи и в зависимости от
предполагаемых значений
 и
и попытаемся построить графики токов и
напряжений. Возможны 3 случая в зависимости
от того, что получится в подкоренном
выражении в формуле для
попытаемся построить графики токов и
напряжений. Возможны 3 случая в зависимости
от того, что получится в подкоренном
выражении в формуле для :
:
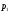 и
и отрицательны и различны,
отрицательны и различны, ;
; и
и отрицательны и совпадают,
отрицательны и совпадают, ;
;
 и
и представляют собой пару комплексно
сопряженных чисел,
представляют собой пару комплексно
сопряженных чисел, .
.
Периодический характер процесса.
Данный случай характеризуется выражением
 ,
,
т.е. корни характеристического уравнения
 и
и - комплексно сопряженные величины.
Введем следующие обозначения:
- комплексно сопряженные величины.
Введем следующие обозначения:
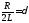 ,
, .
.
Тогда


 .
.
Найдем выражение для тока в контуре:
 .
.
Получили периодическую зависимость тока от времени, отсюда и название случая.
 .
.
Введем
новые переменные
 и
и следующим образом:
следующим образом:
1)

2) .
Разделим
и умножим выражение для
 на
на :
:

 .
.
Найдем оставшуюся временную зависимость на конденсаторе. Имеем:
 ,
,
тогда
 .
.
Заметим, что в данном случае мы имеем
две постоянных времени.
График зависимости тока от времени будет иметь вид:
 .
.
В общем виде график такого плана строится следующим образом. Очевидно, у этого графика есть 2 асимптоты – огибающие синусоиды, ведь график функции представляет собой синусоиду, амплитуда которой уменьшается по экспоненциальному закону.
Первая постоянная времени
 характеризует асимптоты-экспоненты, а
вторая -
характеризует асимптоты-экспоненты, а
вторая - - частоту синусоидальной функции.
- частоту синусоидальной функции.
Теперь займемся построением графиков непосредственно токов и напряжений. Выпишем для наглядности полученные временные зависимости:

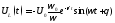

График тока (а значит и напряжения на резисторе) будет иметь такую же структуру, как только что рассмотренный, только взятый с противоположным знаком (действительно, при замыкании контура конденсатор начинает разряжаться).
Из формулы следует, что график напряжения на индуктивности начинается из отрицательной области (в начальный момент времени), а график напряжения на конденсаторе – из такого же по модулю и противоположного по знаку значения. Напряжение на индуктивности уже достигло своего максимального значения и после коммутации спадает (по модулю), а на емкости – только приближается к максимальному значению. Исходя из этих соображений, можно качественно построить графики.

Отметим, что если
 ,
то
,
то ,
, ,
т.е. график будет без затуханий:
действительно, мощность не будет
рассеиваться на активном элементе.
,
т.е. график будет без затуханий:
действительно, мощность не будет
рассеиваться на активном элементе.
