
edisk_files / PraktykumLA+AG
.pdf


10. Задачі на прямі й площини |
153 |
|
|
|
5 ( 1) |
2, |
|
|
|
x 7 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
P L M |
|
( 1) |
(2; 3;1). |
||
|
: y 4 |
3, M |
|||
|
|
|
|
|
|
|
|
|
4 ( 1) |
1; |
|
|
|
z 5 |
|
||
|
|
|
|
|
|
Коментар. Стислий загальний розв’язок задачі:
Площина P n і пряма L s перетинатимуться лише в одній точці, якщо
P L n s (n, s ) 0.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(r |
) L, |
|
|
r |
ts , |
|
||||||||||||
M |
|
r |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
M ( |
|
) P |
( |
|
|
|
|
, |
|
) |
0 |
|||||||
r |
r |
r |
n |
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
(r0 ts r1,n) 0 t(s ,n) (r0 r1,n) 0;
|
( |
r1 |
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|||||||
t |
r0,n) |
|
|
|
|
r1 |
r0,n) |
s . |
||||||||||||||||||||||
r |
r |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
(s ,n) |
|
(s ,n) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
10.5. Знайти проекцію точки M0(1;0;1) на площину P : 4x z 12 0.
Розв’язання.
[Крок 1.] Пряма L, яка проектує точку M0 на площину P пе- |
L |
|||
рпендикулярна до P, а отже має параметричні рівняння (див. |
M0 |
|||
зад. 10.3) |
|
|
|
P |
|
|
|
M |
|
|
|
1 4t, |
|
|
|
|
|
||
x |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
L : y |
|
Рис. до зад. 10.5 |
||
|
|
|
|
|
|
|
1 t. |
|
|
z |
|
|
||
|
|
|
|
|
[Крок 2.] Знайдімо точку M |
— проекцію точки M0 — точку перетину прямої |
|||
L і площини P (див. зад. 10.4): |
|
|
||
|
|
z 12 0, |
|
|
4x |
|
|
||
|
|
|
|
|
|
1 4t, |
|
|
|
x |
|
|
||
|
|
|
M ( 3; 0; 0). |
|
M : |
0, |
|
||
y |
|
|
||
|
|
|
|
|
|
1 t |
|
|
|
z |
|
|
||
|
|
|
|
|


|
|
|
|
|
|
|
|
|
10. Задачі на прямі й площини |
|
155 |
|||||||||||
10.8. Знайти |
точку, |
що |
|
симетрична |
точці |
M1(2; 5;7) щодо |
прямої |
|||||||||||||||
L : x 5 |
y 4 z 6 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Крок 1.] Знайдімо проекцію точки M1 на пряму L — точку M1 (див. зад. 10.6): |
||||||||||||||||||||||
|
|
|
|
|
|
|
M (3; 2;2). |
|
|
|
|
|
|
|
L |
|||||||
[Крок 2.] Точка M |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
M M |
|
|
|
|
||||
2 |
|
поділяє відрізок |
у відношенні |
|
M2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|||
2 [2.6.7], отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
1 |
M |
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
r |
|
r |
r |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. до зад. 10.8 |
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 2 |
5 |
|
1 |
M (4;1; 3). |
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
7 |
|
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Коментар. Точку M2 таку, що |
|
|
|
|
|
|
|
|
|
називають симетричною |
|
|
|
|
|||||||
|
M1M2 |
|
|
|
M1M1 |
|
|
|||
точці M1 щодо прямої L, де M — проекція точки M1 |
на пряму L. |
|||||||||
10.9. Знайти точку, що симетрична |
точці M1(1;3; 4) щодо площини |
|||||||||
P : 3x y 2z 0.
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
[Крок 1.] Знайдімо проекцію точки M1 |
на площину P — точ- |
M1 |
|||||||||||||||||||||||||
ку M (див. зад. 10.5): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
||||||||
1 |
|
|
|
|
|
|
|
|
M ( 2;2; 2). |
|
|
|
|
|
|
P |
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
[Крок 2.] Точка |
|
M |
|
поділяє |
|
|
відрізок |
M M |
у відношенні |
|
|||||||||||||||||
|
2 |
|
|
Рис. до зад. 10.9 |
|||||||||||||||||||||||
2 , отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
r |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
r |
2 |
|
|
3 |
|
( 5;1; 0). |
|
|
||||||||||||||
|
|
|
|
|
2 |
|
|
1 |
M |
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Коментар. Точку M2 |
називають симетричною точці M1 щодо площини P, |
||||||||||||||||||||||||||
якщо |
|
|
|
|
|
|
|
|
|
, |
де M |
|
|
— проекція точки M1 на площину P. |
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
M1M2 |
|
M1M1 |
|
|
|
|
||||||||||||||||||||


|
|
|
|
|
|
|
|
|
|
10. Задачі на прямі й площини |
157 |
||||
[Крок 2.] Площину P1, яка містить пряму L1 |
і перпендикулярна до площини |
||||||||||||||
P |
|
(P) задамо рівнянням |
|
|
|
|
|||||||||
n |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
x 6 |
y 1 z 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
( |
|
|
|
, |
|
|
|
) 0 |
1 |
2 |
1 |
|
0 |
|
|
r |
r1 |
s1, |
n |
||||||||||
|
2 |
1 |
4 |
|
|
||||||||||
|
|
|
(x 6) 9 (y 1) 6 (z |
10) ( 3) |
0; |
||||||||||
P1 : 3x 2y z 6 0.
[Крок 3.] Площину P2, яка містить пряму L2 і перпендикулярна до площини
P n(P) задамо рівнянням
|
|
|
|
|
|
|
|
|
|
x 4 |
y 3 |
z 4 |
|
( |
|
|
|
|
, |
|
|
|
) 0 |
7 |
2 |
3 |
0 |
r |
r2 |
s2, |
n |
||||||||||
|
|
|
|
|
|
2 |
1 |
4 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 4) 5 (y 3) ( 34) (z 4) ( 11) 0; P2 : 5x 34y 11z 38 0.
[Крок 4.] Шукану пряму L — спільний перпендикуляр до прямих L1 та L2 —
задамо перетином двох площин P1 та P2 :
3x 2y z 6 0, L :
5x 34y 11z 38 0.
Коментар. Можлива така схема розв’язання цієї задачі.
[Крок 1.] За нормальний вектор площини P, яка проходить через пряму
L1(M1;s1) паралельно прямій L2(M2 ;s2 ) (див. зад. 10.2 та Коментар до зад. 9.8)
візьмімо вектор
n(P) [s1,s2 ].
[Крок 2.] Площину P1, яка містить пряму L1 і перпендикулярна до площини
P [s1, s2 ] задамо рівнянням
(r r1, s1,[s1,s2 ]) 0.
[Крок 3.] Площину P2, яка містить пряму L2 і перпендикулярна до площини
P [s1, s2 ] задамо рівнянням
( |
|
|
|
|
|
|
|
|
|
s2 ]) 0. |
||||||
r |
r2, s2,[ |
s1, |
||||||||||||||
[Крок 4.] Шукану пряму L — спільний перпендикуляр до прямих L1 та L2 — |
||||||||||||||||
задамо перетином двох площин P1 |
та P2 |
: |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
]) 0, |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
(r r , s ,[s , s |
2 |
|||||||||||||||
|
1 1 |
|
1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
(r r , s ,[s , s ]) 0.
2 2 1 2



 n
n 
 1
1
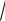 1 4 36
1 4 36 
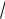 41.
41.