- •Федеральное агентство морского и речного транспорта
- •Предисловие
- •Лекция 1 Элементы геометрической оптики.
- •Основные законы геометрической оптики.
- •Тонкие линзы. Изображение предметов с помощью собирающей линзы.
- •Лекция 2 Волновая оптика
- •Интерференция света.
- •Получение когерентных источников. Оптическая разность хода.
- •Расчет интерференции в опыте Юнга.
- •Лекция 3. Интерференция света
- •Интерференция в тонких пленках
- •2. Кольца Ньютона
- •3. Применение интерференции
- •Лекция 4. Дифракция света
- •Принцип Гюйгенса – Френеля.
- •Дифракция Френеля на круглом отверстии.
- •Дифракция Френеля на небольшом диске.
- •Лекция 5 Дифракция Фраунгофера
- •Дифракция от одной прямоугольной щели
- •Дифракционная решетка
- •Голография
- •Лекция 6 Поляризация света
- •Естественный и поляризованный свет
- •Поляризация света при отражении. Закон Брюстера.
- •Явление двойного лучепреломления и его особенности. Дихроизм.
- •Природа двойного лучепреломления.
- •Применение поляризованного света.
- •Лекция 7 Распространение света в веществе
- •Дисперсия света.
- •Поглощение света.
- •Рассеяние света.
- •Лекция 8 Тепловое излучение
- •Характеристики теплового излучения.
- •2. Поглощательная и отражательная способности тел.
- •3. 3Аконы теплового излучения.
- •4. Оптическая пирометрия
- •Лекция 9 Фотоэффект
- •Законы внешнего фотоэффекта
- •Уравнение Эйнштейна для фотоэффекта
- •Фотон и его свойства
- •Эффект Комптона
- •Люминесценция, фотолюминесценция и ее основные закономерности
- •Физические принципы устройства приборов ночного видения
- •Лекция 10 Теория атома водорода по Бору
- •Линейчатый спектр атома водорода
- •Модели атома Томсона и Резерфорда
- •Постулаты Бора
- •Спектр атома водорода по Бору
- •Лекция 11 Элементы квантовой механики
- •Корпускулярно-волновой дуализм свойств вещества. Гипотеза де Бройля.
- •Природа волн де Бройля
- •Соотношение неопределенностей Гейзенберга
- •Уравнение Шредингера. Волновая функция.
- •Физический смысл волновой функции
- •Лекция 12 Атом водорода в квантовой механике
- •Уравнение Шредингера для атома водорода
- •Квантовые числа.
- •Спин электрона.
- •Лекция 13 Оптические квантовые генераторы
- •Физические основы работы окг. Спонтанное и индуцированное излучение.
- •Термодинамическое равновесие. Нормальная населенность уровней.
- •Неравновесное состояние. Инверсия населенности уровней.
- •Рубиновый лазер
- •Газовый лазер
- •Лекция 14 Атомное ядро и основы ядерной энергетики
- •Состав и характеристики ядра
- •Энергия связи и дефект масс
- •Ядерные силы
- •Радиоактивность
- •Лекция 15
- •Реакция деления тяжелых ядер
- •Цепная реакция деления
- •Управляемая цепная реакция. Ядерные реакторы.
- •Термоядерная реакция синтеза легких ядер
- •Принципиальная схема устройства термоядерной бомбы
- •Проблемы управления термоядерной реакцией
- •Лекция 16 Элементарные частицы
- •Космические лучи
- •Элементарные частицы
- •Основные свойства.
- •Характеристики элементарных частиц.
- •Мюоны и их свойства.
- •Мезоны и их свойства.
- •Частицы и античастицы
- •Классификация элементарных частиц. Кварки.
Лекция 12 Атом водорода в квантовой механике
Уравнение Шредингера для атома водорода
Самой простой задачей квантовой механики является задача о движении электрона в кулоновском поле ядра. Это задача об атоме водорода и водорода подобных ионов: однократно ионизированный гелий и однократно ионизированный литий.
Потенциальная энергия взаимодействия электрона с ядром:
|
|
(1) |
где
![]() - заряд ядра (для атома водорода
- заряд ядра (для атома водорода![]() ),
),![]() - расстояние между электроном и ядром.
- расстояние между электроном и ядром.
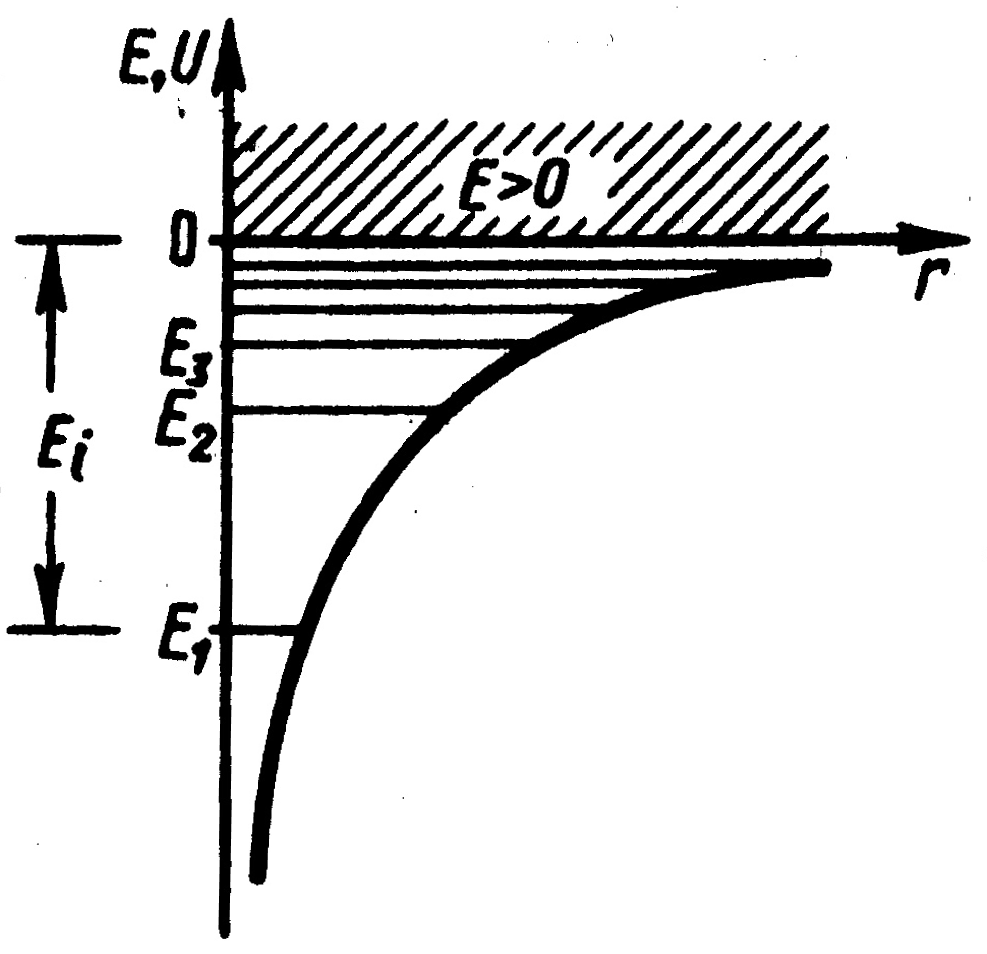
Графически функция
![]() изображена на рис.1. С уменьшением
изображена на рис.1. С уменьшением![]() функция
функция![]() убывает (возрастает по модулю).
убывает (возрастает по модулю).
|
Рис.1. |
Состояние электрон в атоме водорода
описывается волновой функцией
![]() ,
удовлетворяющей стационарному уравнению
Шредингера, учитывающему выражение
(1):
,
удовлетворяющей стационарному уравнению
Шредингера, учитывающему выражение
(1):
|
|
(2) |
где
![]() - масса электрона, а
- масса электрона, а![]() - полная энергия электрона в атоме.
- полная энергия электрона в атоме.
Уравнение (2) имеет решения, удовлетворяющие требования однозначности, конечности и непрерывности волновой функции только при следующих собственных значениях энергии:
|
|
(3) |
Таким образом, из решения уравнения
Шредингера следует, что энергия электрона
в атоме квантуется. Формула (3) дает набор
дискретных значений энергии, совпадающими
со значениями энергии, найденными из
спектров. Возможные значения показаны
на рис.1. в виде горизонтальных прямых.
Самый низкий уровень энергии
![]() называется основным, все остальные –
возбужденными. При
называется основным, все остальные –
возбужденными. При![]() движение электрона является связанным:
по мере роста главного квантового числа
энергетические уровни располагаются
теснее и при
движение электрона является связанным:
по мере роста главного квантового числа
энергетические уровни располагаются
теснее и при![]()
![]() .
При
.
При![]() движение электрона является свободным.
Область непрерывного спектра
движение электрона является свободным.
Область непрерывного спектра![]() соответствует ионизированному атому.
Энергия ионизации атома водорода равна:
соответствует ионизированному атому.
Энергия ионизации атома водорода равна:
|
|
Квантовые числа.
Собственные функции
![]() ,
являющиеся решениями уравнения Шредингера
зависят от трех квантовых чисел:
,
являющиеся решениями уравнения Шредингера
зависят от трех квантовых чисел:![]() ,
,![]() и
и![]() .
.![]() - главное квантовое число, определяет
энергетические уровни электрона в атоме
и принимает значения
- главное квантовое число, определяет
энергетические уровни электрона в атоме
и принимает значения![]() 1,
2, 3,…
1,
2, 3,…
![]() - орбитальное квантовое число, оно
связано с квантованием момента импульса
электрона (механического орбитального
момента). То есть орбитальный момент не
может быть произвольным, а принимает
дискретные значения, определяемые
формулой:
- орбитальное квантовое число, оно
связано с квантованием момента импульса
электрона (механического орбитального
момента). То есть орбитальный момент не
может быть произвольным, а принимает
дискретные значения, определяемые
формулой:
|
|
(4) |
При данном значении
![]()
![]() - принимает значения
- принимает значения
|
|
Всего
![]() значений.
значений.
![]() - магнитное квантовое число, связанное
с квантованием проекции момента импульса
на выбранное направление (обычно в
направлении магнитного поля по оси
- магнитное квантовое число, связанное
с квантованием проекции момента импульса
на выбранное направление (обычно в
направлении магнитного поля по оси![]() ):
):
|
|
(5) |
Магнитное квантовое число может принимать следующие значения:
|
|
Всего
![]() значений.
значений.
Таким образом, вектор момента импульса
электрона может иметь такие ориентации
в пространстве, при которых его проекция
на выделенное направление (ось
![]() )
принимает квантованные значения согласно
формуле (5). Это означает, что в магнитном
поле уровень с орбитальным квантовым
числом
)
принимает квантованные значения согласно
формуле (5). Это означает, что в магнитном
поле уровень с орбитальным квантовым
числом![]() расщепляется на
расщепляется на![]() подуровней. Это было в 1896 году
экспериментально обнаружено голландским
физиком Зееманом.
подуровней. Это было в 1896 году
экспериментально обнаружено голландским
физиком Зееманом.
Из формулы (3) следует, что каждому
значению
![]() соответствует энергия
соответствует энергия![]() .
Каждой энергии
.
Каждой энергии![]() соответствует несколько волновых
функций
соответствует несколько волновых
функций![]() отличающихся значениями
отличающихся значениями![]() и
и![]() .
То есть при одном и том же значении
энергии атом водорода может быть в
нескольких различных состояниях. Найдем
число состояний с одинаковой энергией
.
То есть при одном и том же значении
энергии атом водорода может быть в
нескольких различных состояниях. Найдем
число состояний с одинаковой энергией![]() .
Так как при данном
.
Так как при данном![]() орбитальное квантовое число
орбитальное квантовое число![]() изменяется от
изменяется от![]() до
до![]() ,
а каждому
,
а каждому![]() соответствует
соответствует![]() значений
значений![]() ,
то число различных состояний равно:
,
то число различных состояний равно:
|
|
(6) |
В квантовой механике состояния с
различными
![]() обозначают буквенными символами как и
спектроскопии:
обозначают буквенными символами как и
спектроскопии:
![]() -s-состояние
-s-состояние
![]() -p-состояние
-p-состояние
![]() -d-состояние
-d-состояние
![]() -f-состояние
-f-состояние
При записи квантового состояния сначала
пишут численное значение
![]() ,
а затем буквенное
,
а затем буквенное![]() .
Например, состояние
.
Например, состояние![]() и
и![]() обозначают
обозначают![]() f.
f.
Квадрат модуля волновой функции
![]() определяет вероятность обнаружения
электрона в единице объема. Электрон
при своем движении как бы «размазан»,
образуя электронное облако, плотность
которого характеризует вероятность
нахождения электрона в различных точках
атома.
определяет вероятность обнаружения
электрона в единице объема. Электрон
при своем движении как бы «размазан»,
образуя электронное облако, плотность
которого характеризует вероятность
нахождения электрона в различных точках
атома.
Квантовые числа
![]() и
и![]() характеризуют размер и форму электронного
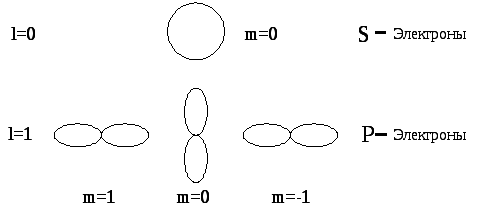
облака, а квантовое число
характеризуют размер и форму электронного
облака, а квантовое число![]() - его ориентацию в пространстве. На
рис.2. для примера приведено распределение
электронной плотности (формы электронного
облака) для состояний атома водорода
при
- его ориентацию в пространстве. На
рис.2. для примера приведено распределение
электронной плотности (формы электронного
облака) для состояний атома водорода
при![]() и
и![]() .
Как видно из рисунка, оно зависит от
.
Как видно из рисунка, оно зависит от![]() ,
,![]() и
и![]() .
При
.
При![]() электронное облако имеет форму шара,
при
электронное облако имеет форму шара,
при![]() - форму гантели.
- форму гантели.
|
Рис.2. |
Радиус шара в 1sсостоянии равен радиусу первой орбиты Бора. По теории Бора электрон может находиться только на орбите, в квантовой механике – в любом месте пространства, но с разной плотностью.