2. Модели атома Томсона и Резерфорда

Для объяснения спектров атомов были предложены различные модели атомов.

В 1903 году английский физик Томсон предложил модель атома, представляющую собой непрерывно заряженный положительный шар радиусом м, в которую вкраплены электроны. Суммарный отрицательный заряд, равен положительному заряду шара и поэтому атом нейтрален.

Однако, в 1911 году английский физик Резерфорд своими опытами по рассеянию - частиц опровергает утверждение Томсона о непрерывном распределении положительного заряда внутри шара. В своем опыте Резерфорд обнаружил, что при прохождении- частиц через золотую фольгу толщиной 1мкм основная их часть испытывает незначительные отклонения, но некоторые- частицы (примерно одна из 20000) отклоняются на углы равные. На основании этих исследований Резерфорд предложил планетарную модель атома. Согласно этой модели в центре атома находится положительно заряженное ядро, имеющие размерым. Вокруг ядра по орбитам вращаются электроны. Число электронов равно заряду ядра.

Столкновение с ядром - частиц происходят крайне редко из-за его малых размеров. Но планетарная модель оказалась в противоречии с законами классической механики и электродинамики:

1. Вращающийся электрон имеет заряд, движется он ускоренно и поэтому должен излучать. Излучая энергию, он приближается к ядру по спирали. Расчеты показывают, что он упадет на ядро через 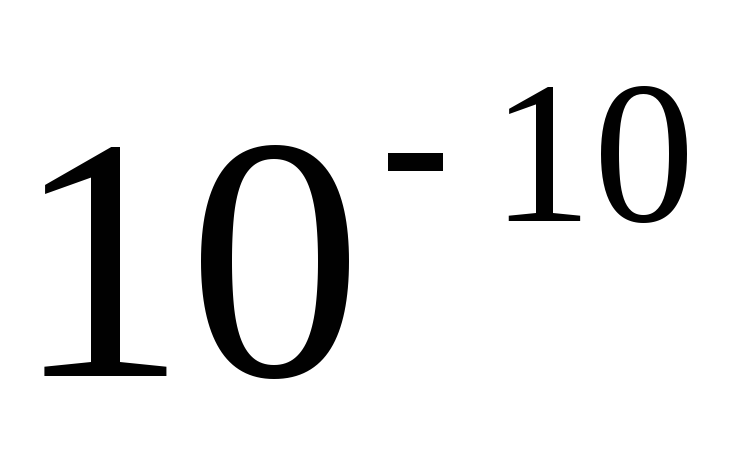с. То есть атом Резерфорда не устойчив.

2. По мере приближения к ядру радиус траектории электрона убывает. Момент инерции его 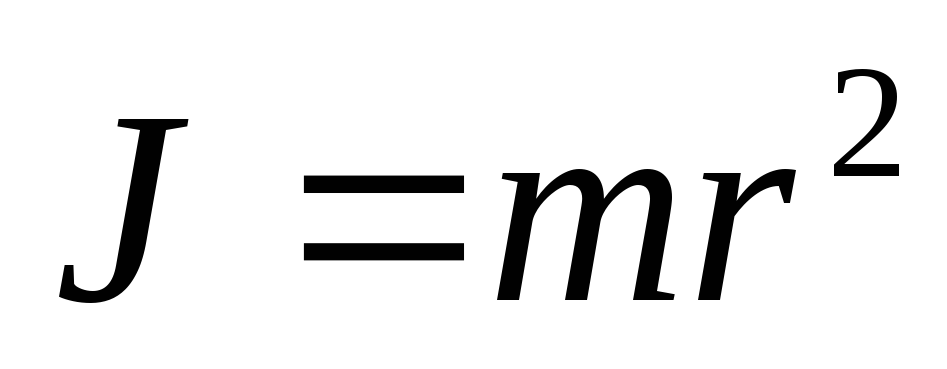убывает. Но по закону сохранения момента импульса. Так какнепрерывно убывает,должно расти. Поэтому спектр излучения должен быть сплошным, а не линейчатым.

Таким образом, планетарная модель атома не могла объяснить ни устойчивость атома, ни характер спектра.

3. Постулаты Бора

Для того, чтобы объяснить линейчатые спектры атомов датский физик Нильс Бор в 1913 году вводит два постулата.

Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся во времени) состояния, в которых он не излучает энергию. Энергии этих состояний образуют дискретный ряд: ,, …,. Стационарным состояниям атома соответствуют орбиты, по которым движутся электроны. Хотя электроны движутся по стационарным орбитам с ускорением, они не излучают и не поглощают энергию.

В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные значения момента импульса, удовлетворяющие условию:

,1, 2, 3,…,

где - масса электрона,- его скорость по-ой орбите радиуса,.

Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) квант с энергией:

.

При происходит излучение фотона (переход из состояния с большей энергией в состояние с меньшей энергией), при- поглощение фотона (переход атома в состояние с большей энергией).

Набор возможных дискретных частот определяет линейчатый спектр атома.

4. Спектр атома водорода по Бору

Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем, состоящих из ядра с зарядом и одного электрона (ионы,), а также теоретически вычислить постоянную Ридберга.

Рассмотрим движение электрона в водородоподобной системе по стационарным круговым орбитам.

Решая совместно уравнение 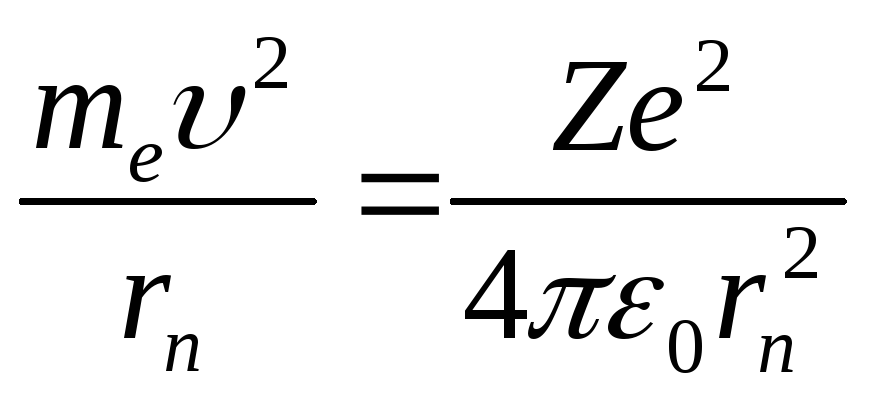, вытекающие из планетарной модели Резерфорда, и уравнение для момента импульса стационарных орбит, получим выражение для радиуса-ой стационарной орбиты. Помножим правую и левую часть первого уравнения на:

.

Возведем обе части второго уравнения , в квадрат:

.

Из этих уравнений можно выразить значение радиуса:

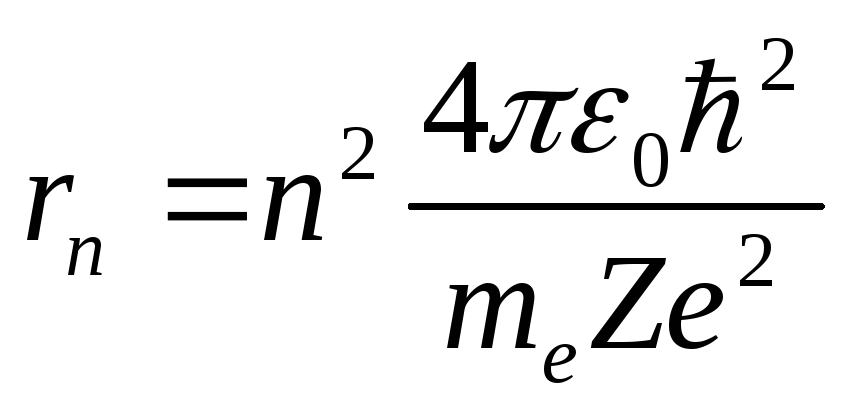,1, 2, 3, …

Из этого выражения следует, что радиусы орбит растут пропорционально квадрату целых чисел. Для водорода () радиус первой электронной орбиты () равен:

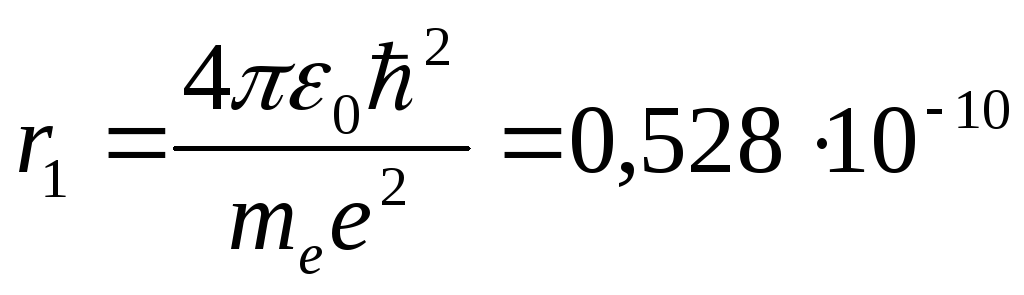м,

что соответствует размерам атома, рассчитанным из молекулярно-кинетической теории газов.

Теперь подсчитаем полную энергию электронов, находящихся на стационарных орбитах. Полная энергия электрона складывается из его кинетической энергии и потенциальной энергии в электростатическом поле ядра:

.

Учитывая уравнение и выражение для радиуса-ой орбиты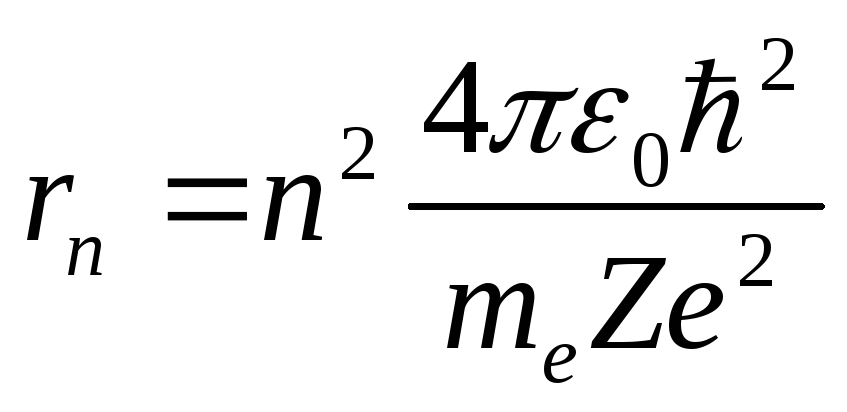, получим выражение для полной энергии в виде:.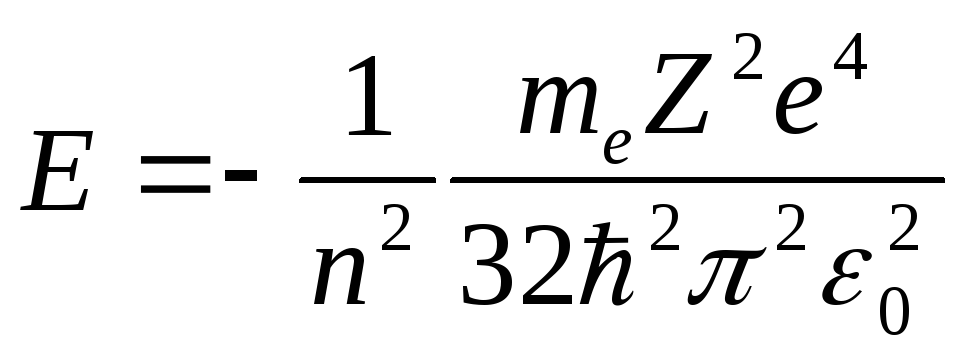

Учитывая, что , окончательно получим:

.

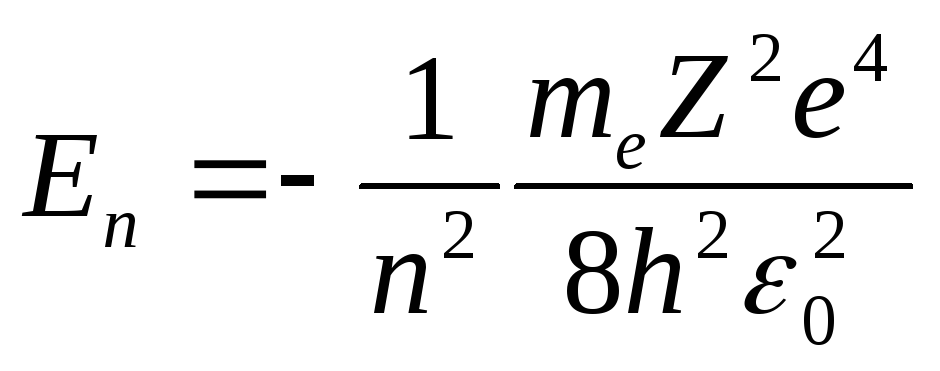Энергетические состояния атома образуют последовательность энергетических уровней, меняющихся в зависимости от значения . Число, определяющее энергетические уровни атома, называется главным квантовым числом. Состояние сназывается основным, состояния с- возбужденными. Придаваяразличные целочисленные значения, получим для атома водорода () возможные уровни энергии.

Энергия атома водорода с увеличением возрастает (уменьшается ее отрицательная величина) и энергетические уровни сближаются с границе, соответствующей значению. Минимальная энергия атома водорода равнаэВ при, максимальная энергия равна нулю при. Значениесоответствует ионизации атома (отрыву от него электрона).

Согласно второму постулату Бора при переходе атома водорода из стационарного состояния в состояние с меньшей энергиейиспускается квант с энергией:

.

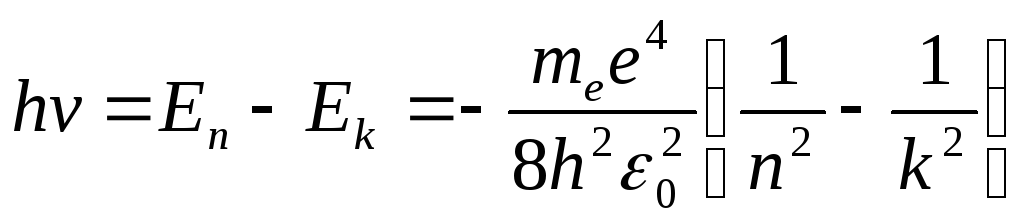Откуда частота излучения равна:

,

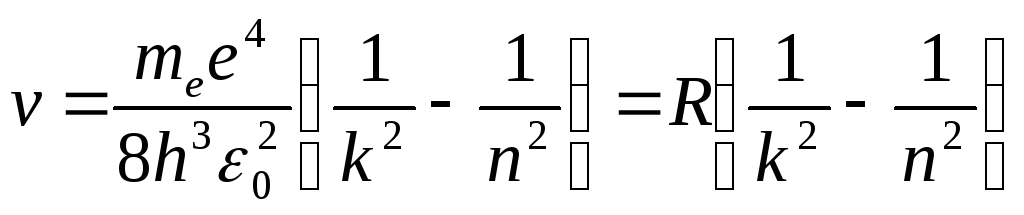где .

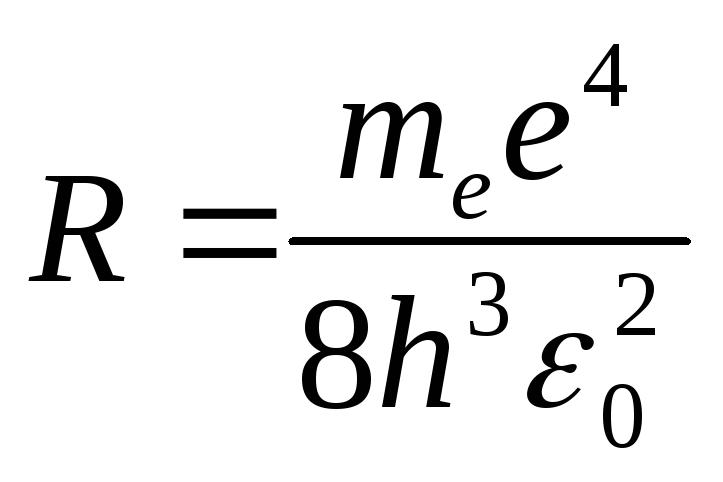Величина , рассчитанная по этой формуле, совпала с экспериментальным значением постоянной Ридберга в эмпирической формуле для атома водорода.

Подставляя и2, 3, 4,… получаем серию Лаймана (переходы с возбужденных уровнейна основной). При подстановке2, 3, 4, 5, 6 и соответствующих им значенийполучим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри.

Спектр поглощения атома водорода является также линейчатым, но содержит только серию Лаймана. Так как свободные атомы водорода находятся в основном состоянии, то при сообщении атомам энергии извне могут наблюдаться лишь переходы из основного состояния в возбужденные.

Таким образом, теория Бора позволила вычислить частоты спектральных линий атома водорода и водородоподобных систем, но не могла объяснить их интенсивности и почему вероятность различных переходов разная. Теория Бора не смогла объяснить спектр атома гелия, содержащего два электрона в поле ядра. Теория Бора содержит внутренние противоречия: она основывается на классической физике, но вводит квантовые постулаты. Теория Бора является переходной от классической физики к квантовой.