
РГР по математике
.pdf1
Министерство образования и науки Российской Федерации Коломенский институт (филиал)
федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Московский государственный машиностроительный университет (МАМИ)» в г. Коломне Московской области
Е.Ф. КАЛИНИЧЕНКО
МАТЕРИАЛЫ
расчетно-графических работ по математике
для студентов 1 курса специальностей менеджмент и государственное и муниципальное управление
Издание первое
Коломна КИ (ф) МГОУ – 2014
2
УДК 512.64 (075);
ББК22.11
Рецензенты:
кандидат технических. наук, доцент кафедры строительного производства КИ (ф) МАМИ Брыль С.В.
Калиниченко Е.Ф.
МАТЕРИАЛЫ расчетно-графических работ по математике. 1-е изд., –
Коломна: КИ (ф) МАМИ, 2014, 65 с.
Учебное пособие содержит теорию, задания и требования к выполнению расчетно-графических работ по математике. Предназначено для студентов специальностей «менеджмент» и «государственное и муниципальное управление» технических университетов дневной формы обучения.
Рассмотрено на заседании кафедры строительного производства 9.10.2014г., протокол №3/2014

3
1.Расчетно-графическая работа по математике №1
1.1. Краткая теория
1.1.1. Решение систем линейных уравнений
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
.
Здесь x1, x2, …, xn — неизвестные, которые надо определить. Числа a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов aij системы обозначают номера уравнения i и неизвестного j , при котором стоит этот коэффициент, соответственно.
Система называется однородной , если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Решением системы называют совокупность n чисел c1, c2, …, cn таких, что подстановка каждого ci вместо неизвестного xi в систему, обращает
все её уравнения в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Решить систему значит найти все ее решения или показать, что система несовместна.
Систему линейных уравнений можно представить в матричной форме
или AX = B.
Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной матрицей системы.
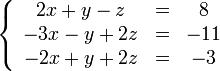
4
Методы решения.
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения, когда с помощью элементарных преобразований расширенная матрица системы приводится к треугольному виду. Записав систему, соответствующую треугольному виду, последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Методом Гаусса может быть решена любая система уравнений.
Пример 1. Решить методом Гаусса следующую систему:
Решение. Прямой ход. Расширенная матрица системы имеет вид:
|
|
2 |
1 |
1 |
8 |
|
|
|
A |
|
3 |
1 |
2 |
11 |
. К первой строке прибавим вторую, получим: |
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
2 |
3 |
|
|
|
|
|
|
|
||||
1 |
|
0 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
. Ко второй строке прибавим первую строку, умноженную |
||
|
3 |
|
1 |
2 |
11 |
|||
|
2 |
|
1 |
2 |
|
|
|
|
|
|
3 |
|
|
|
|||
на (-3), а к третьей прибавим первую, умноженную на (-2), получим матрицу:
1 |
0 |
1 |
3 |
|
|
|
|
|
|
|
|
||
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
0 |
. |
К |
третьей строке |
прибавим |
первую строку, |
получим |
||||||
|
0 |
1 |
0 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
0 |
1 |
3 |
|
|
|
|
||
матрицу: |
|
0 |
1 |
1 |
2 . Матрица |
приведена |
к |
треугольному |
виду. Ей |
||||
|
|
|
|
0 |
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x z 3, |
|
|
|
|
соответствует |
система: |
y z 2, |
В результате |
мы привели |
исходную |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 1. |
|
систему к треугольному виду, тем самым, закончив первый этап алгоритма.
Обратный ход. Из последнего уравнения находим переменную z и подставляем ее значение в первое и второе уравнения, получаем систему:
x ( 1) 3,y ( 1) 2,
z 1.

5
Из второго уравнения находим переменную y и подставляем ее значение в первое уравнение, получаем систему:
x ( 1) 3, |
|
|
|
y 3, |
Из второго уравнения находим переменную x . Таким образом, |
|
||
|
|
|
|
z 1. |
|
исходная система решена x 2; y 3; z 1.
Метод Крамера. Этот метод применяют для систем, у которых число уравнений равно числу неизвестных.
Теорема Крамера. Пусть =| A | - определитель матрицы системы, а i -
определитель матрицы системы, полученный из матрицы A заменой i того столбца столбцом свободных членов. Тогда, если 0 , то система имеет
единственное решение, определяемое по формулам Крамера |
xi |
|
i |
. Если |
|
||||
|
|
|
|
|
0 и все i 0 , то система имеет бесконечно много решений. Если 0 и хотя бы один из определителей i 0 , то система не имеет решений.
Пример 2. Решить методом Крамера следующую систему:
Решение. Определители:
Пример 3. Решите систему уравнений
|
x1 2x2 x3 8, |
|
2 |
1 |
|
||
|
1 |
|
|||||
|
|
3x3 5, |
|
2 |
|
3 |
6 6 10 3 8 15 0, |
2x1 3x2 |
3 |
||||||
|
x1 5x2 |
2x3 3. |
|
1 |
5 |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
6 |
|||
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
8 |
|
|
|
|
||||
1 |
|
|
5 |
3 |
|
3 |
|
48 18 25 9 120 20 0, |
||
|
|
3 |
5 |
|
2 |
|
|
|
||
|
|
|
8 |
1 |
|
|||||
|
|
|
1 |
|
||||||
2 |
2 |
5 |
3 |
10 24 6 5 32 9 0, |
||||||
|
|
|
|
1 |
3 |
2 |
|
|||
|
|
2 |
|
8 |
|
|
|
|||
|
|
1 |
|
|
|
|
||||
3 |
2 |
3 |
5 |
9 80 10 24 12 25 0. |
||||||
|
|
|
|
1 |
5 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, система имеет бесконечное множество решений.
Найдем эти решения. Так как определитель системы 0 , то ранг матрицы
системы меньше 3. |
|
|
|
|
1. Выделим минор второго порядка M 2 |
|
2 |
|
3 4 7 0 . Так как минор |
1 |
|
|||
|
2 |
3 |
|
|
|
|
|
|
|
второго порядка не равен нулю, то ранг матрицы системы равен двум.
2. Выделим подсистему, коэффициенты при переменных которой входят в
минор M 2 0 |
|
x1 2x2 x3 8, |
|||||
|
2x |
3x |
|
3x |
|
5. |
|
|
|
2 |
3 |
||||
|
1 |
|
|
|
|||
3. Неизвестные x1 , x2 , коэффициенты при которых входят в минор M 2 0
являются базисными, неизвестными, неизвестная x3 , коэффициенты при которой не входят в минор, является свободной неизвестной, переносим
x1 2x2 x3 8, |
|||||||
ее в правую часть системы: |
2x |
3x |
|
3x |
|
5. |
|
|
2 |
3 |
|||||
1 |
|
|
|
||||
4. Решаем полученную подсистему методом Крамера при произвольных
|
значениях свободной неизвестной x3 |
t , где t R . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
x1 2x2 t 8, |
|
|
|
|
|
|
|
|
|
|
M 2 |
|
|
|
3 |
4 |
7 |
0 , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|||||||||||||||||||||
|
|
|
|
|
3x |
|
3t 5. |
|
|
|
|
|
|
|
|
|
|
|
2 3 |
||||||||||||||
|
|
|
2x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
(8 t) |
|
2 |
|
24 3t 6t 10 34 9t , |
|
2 |
|
1 (8 t) |
|
3t 5 16 2t t 11 |
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
(3t 5) |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
(3t 5) |
|
|
|
|
|
|
|
|
|
|||||
Тогда по формулам Крамера |
x |
1 |
|
34 |
|
9t |
, x |
|
|
2 |
|
11 |
|
t |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
7 |
7 |
|
2 |
|
|
|
7 |
|
7 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
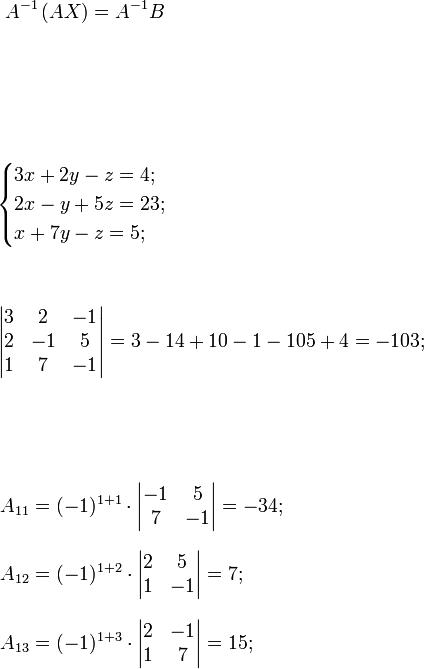
7 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
34 |
|
|
9 |
|
t, |
|||
|
|
|
|
|
|
||||||
|
1 |
7 |
|
|
7 |
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Окончательно имеем решение: x |
|
|
11 |
|
1 |
t, где t R . |
|||||
2 |
|
|
|||||||||
|
|
|
7 |
|
|
7 |
|
|
|||
|
|
|
x3 t. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матричный метод. Этот метод применяют для систем, у которых число уравнений равно числу неизвестных и определитель матрицы системы
отличен от нуля |
. |
Умножим |
матричное уравнение AX = B слева на A − 1 — матрицу, |
обратную к матрице A:
Так как A − 1A = E, получаем X = A − 1B.
Правая часть этого уравнения даст столбец решений исходной системы.
Пример 4. Решить матричным методом систему:
Решение. Сначала убедимся в том, что матрицы системы не равен нулю.
Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.
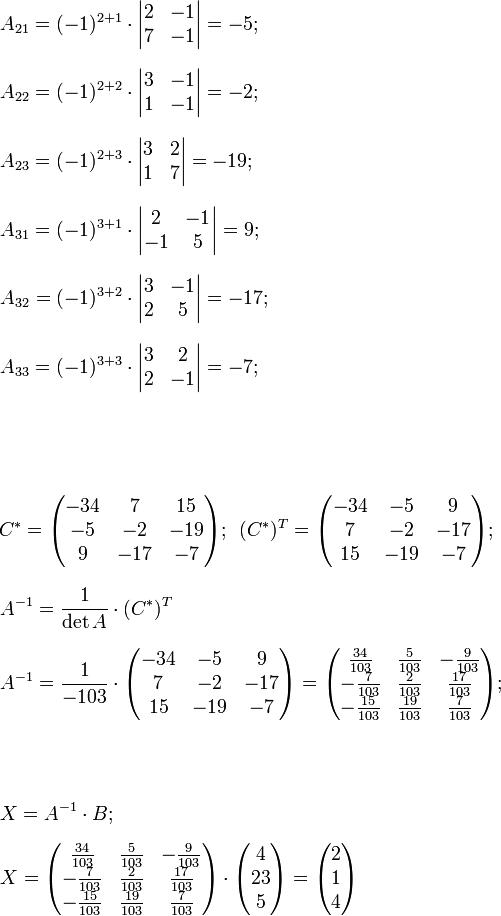
8
Далее найдём присоединенную матрицу C , транспонируем (строки сделаем столбцами) её и подставим в формулу для нахождения обратной матрицы
Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов B .
Итак, x=2; y=1; z=4.
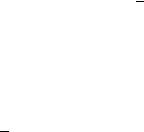
9
1.1.2. Элементы матричного анализа
Векторы на плоскости и в пространстве. Любой отрезок прямой имеет две концевые точки. Если одна из них принята за начало отрезка, а другая — за конец, то такой отрезок называется вектором. Векторы обычно
обозначаются двумя буквами |
со стрелкой, например, |
|
где |
первая |
||||
AB |
||||||||
буква A обозначает начало, |
а вторая |
буква |
B |
— конец вектора |
или |
|||
|
|
|
|
|
|
|
|
|
жирными буквами, например a. Длина вектора a |
AB |
, обозначаемая |
| a | |
или |
||||
|
|
|
|
|
|
|
|
|
| AB | — это длина отрезка АВ. |
|
|
|
|
|
|
|
|
Два вектора считаются |
равными, |
если они имеют |
равные |
длины, |
||||
параллельны и направлены в одну сторону. |
|
|
|
|
|
|
|
|
Если векторы заданы своими координатами в базисе e1, |
e2 |
, e3, то |
||||||
действия над ними выполняются по следующим правилам: |
|
|
|
|
||||
1.(x1; y1; z1) + (x2; y2; z2) = (x1 + x2; y1 + y2; z1 + z2).
2.(x1; y1; z1) —(x2; y2; z2) = (x1 — x2; y1 —y2; z1 —z2)
3.λ (x1; y1; z1) = (λx1; λy1; λz1)
Пример 5. По координатам векторов а = (—4; 6; 0), b = (1; —1; 7) найти координаты векторов: а +b; а — b; 5а; 3b — а.
Решение. Используя правила 1—3, получаем:
а +b = (—3;5;7); а — b = (—5; 7; —7);
5а = (—20; 30; 0); 3b — а.= (5; — 6; 21).
Собственные векторы, собственные значения линейного оператора
Ненулевой вектор |
|
называется собственным вектором |
линейного |
||||
x |
|||||||
|
|
|
существует число R , такое, что |
|
|
|
|
оператора |
y |
f ( x) , если |
f ( x) x |
. Число |
|||
называется собственным числом (собственным значением) оператора f ,
соответствующим этому собственному вектору. |
|
|
|
|
Если в некотором базисе оператор |
f имеет матрицу |
A и в том же |
||
|
|
|
|
|
базисе вектор x имеет координатный столбец X , |
то в матричном виде |
|||
оператор AX X или (A E) X 0. |
|
|
|
|
Собственные числа линейного |
оператора |
|
|
- корни |
y f ( x) |
||||
характеристического уравнения | A E | 0.. Для каждого собственного
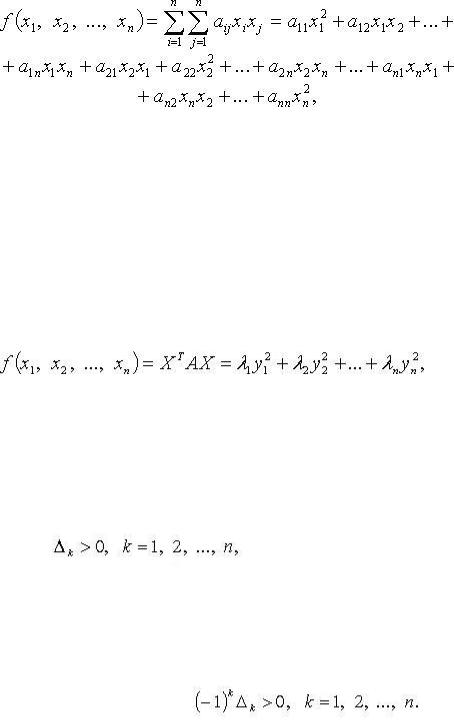
10
значения 0 соответствующие собственные векторы могут быть найдены из матричного уравнения (A 0 E) X 0.или соответствующей ему системы линейных уравнений
( )
{ ( )
( )
Квадратичные формы.
Квадратичная форма переменных x1 , x2 ,...xn - функция
aij - коэффициенты квадратичной формы.
Матрица |
( |
) |
называется |
матрицей |
|
квадратичной формы. |
|
|
|
|
|
Если все несимметричные коэффициенты |
aij 0 |
(i j) , |
то говорят, |
||
что квадратичная форма принимает канонический вид: |
|
|
|||
где 1 , 2 ,... n - собственные значения матрицы A.
Квадратичные формы, |
для которых f (x1 , x2 ,...xn ) 0 для всех x1 , x2 ,...xn |
|||
таких, что |
x 2 |
x |
2 ... x 2 |
0 называется положительно-определенной. |
|
1 |
2 |
n |
|
Квадратичная форма является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны
Квадратичные формы, |
для которых f (x1 , x2 ,...xn ) 0 для всех x1 , x2 ,...xn |
|||
таких, что |
x 2 |
x |
2 ... x 2 |
0 называется отрицательно-определенной. |
|
1 |
2 |
n |
|
Квадратичная форма является отрицательно-определенной тогда и только тогда, когда
