
РГР по математике
.pdf31
3.Расчетно-графическая работа по математике №3
3.1. Краткая теория |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.1.1. Неопределенный интеграл |
|
|
|
|
|
|||||||||
Определение 1. Функция F (x) |
называется первообразной от функции f (x) на |
|||||||||||||
интервале (a;b) , если во всех точках этого интервала F (x) |
дифференцируема |
|||||||||||||
и F (x) = f (x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. Найти первообразную для функции f (x) =x4. |
|
|
|
|
||||||||||
Решение. Из |
определения |
|
1 |
|
следует, что |
функция |
F (x) = |
1 |
x5 |
является |
||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
1 |
|
5 |
|
=x |
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
первообразной, так как (5 x ) |
|
|
|
|
|
|
||||||||
Определение 2. Если F (x) |
является первообразной для |
f (x) , то выражение |
||||||||||||
F (x) +С, называется неопределенным интегралом от |
функции |
f (x) и |
||||||||||||
обозначается |
f (x)dx . |
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, по определению |
|
|
|
|
|
|||||||||
|
|
f (x)dx = F (x) +С, если |
|
|
|
|
|
|||||||
|
|
F (x) = f (x) . |
|
|
|
|
||||||||
При этом, |
знак |
называют знаком интеграла, |
функцию f (x) - |
|||||||||||
подынтегральной |
функцией, |
|
выражение |
f (x) dx – |
подынтегральным |
|||||||||
выражением.
Операцию нахождения неопределенного интеграла называют интегрированием функции. Таким образом проинтегрировать функцию значит найти все ее первообразные.
Свойства неопределенного интеграла Свойство 1. Производная от неопределенного интеграла равна подынтегральной функции
( f (x)dx) = f (x) .
Действительно пользуясь определением 1, имеем ( f (x)dx) =(F(x) C) = f (x) .
Свойство 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
|
|
d( f (x)dx) = f (x) dx. |
|
|
|
В |
самом |
деле, |
f (x)dx = F (x) +С, |
тогда |
d( f (x)dx) =d(F(x)+C)= |
(F (x) C) dx F (x)dx = |
f (x) dx. |
|
|
||
Свойство 3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.
dF (x) = F (x) +С.
32
По определению дифференциала функции dF(x)= F (x) dx, тогда имеем,
dF (x) = F (x)dx f (x)dx = F (x) +С.
Свойство 4. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов
( f1 (x) f2 (x))dx = f1 (x)dx + f2 (x)dx .
По свойству 1 ( ( f1 (x) f2 (x))dx) =f1(x)+f2(x).
С другой стороны ( f1 (x)dx + f2 (x)dx) =9 f1 (x)dx) +( f2 (x)dx) = f1(x)+f2(x).
Так как производные слева и справа равны, то функции отличаются на постоянную величину. В этом смысле и следует понимать свойство 4. Свойство 5. Постоянный множитель можно выносить за знак интеграла, т.е., если С=const, то
Сf (x)dx = С f (x)dx .
Для доказательства найдем производные от левой и правой части
( Сf (x)dx) =Сf(x),
(C f (x)dx) =C ( f (x)dx) =Cf(x).
Производные слева и справа равны, следовательно, функции стоящие слева и справа отличаются только на постоянную величину
Таблица интегралов
1. 0dx C.
2.xn dx nx 1 C , при n 1.
3.x 1dx = dxx =ln|x|+C, при x 0.n 1
4. a x dx = |
a x |
C , при a (0;1) (1; ) , в частности, |
e x dx =ex+C. |
|
ln a |
||||
|
|
|
5.sin xdx =-cosx+C, cos xdx =sinx+C.
6.cosdx2 x = tgx+C, sindx2 x = - ctgx+C.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
C, |
|
||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
arcsin |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
||||||||||||||||||
7. |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
, при x ( a; a). |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||||
|
|
|
2 |
x |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
arccos |
|
|
C, |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
arctg |
x |
|
|
|
|
C, |
|
|||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
8. |
|
|
|
|
|
= |
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||||||||||||||||
a |
2 |
x |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a arcctg a C. |
||||||||||||||||||||
9. |
|
|
dx |
|
|
|
= ln | x |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x |
2 |
a | |
C. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
x |
2 |
a |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10. |
|
dx |
|
|
= |
1 |
|
|
ln | |
x a |
|
| . |
|
|
||||||||||||||||||
x |
2 |
2 |
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
x a |
|
|
|
|
||||||||||||
33
Пример 2. Вычислить интеграл |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3x2 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Решение. |
|
∫ |
|
|
|
|
∫ |
|
|
|
|
. |
|
|
|
Применив |
|
свойство |
5, |
|
|
|
получим |
|||||||||||||||||
|
|
|
|
|
( |
|
) |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где a2= |
5 |
|
||||||
∫ |
|
|
|
∫ |
|
|
|
|
. Применив, |
|
|
|
формулу |
8 таблицы интегралов, |
|
|
||||||||||||||||||||||||
|
|
( |
|
|
) |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
окончательно получаем: ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
√ |
|
|
√ |
√ |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3.1.2. Определенный интеграл
Непосредственное вычисление определенного интеграла связано с трудностями – интегральные суммы имеют громоздкий характер и их трудно преобразовать к виду удобному для вычисления интегралов. По крайней мере, нет общих методов, как это сделать. Каждая задача решалась индивидуально, пока Ньютону и Лейбницу не удалось показать, что вычисление определенного интеграла от функции можно свести к отысканию ее первообразной.
Если функция f (x) интегрируема на отрезке [a,b] , то она интегрируема
x
и на отрезке [a, x] , где x [a,b] , т.е. существует интеграл f (t)dt . Этот интеграл
a
является функцией x , его обозначают
x
Ф(x) = f (t)dt
a
и называют интегралом с переменным верхним пределом. Интеграл с переменным верхним пределом обладает свойствами, сформулированными в следующих теоремах.
x
Теорема 1. Если f (x) - непрерывная на отрезке [a,b] функция и Ф(x) = f (t)dt ,
|
|
a |
|
x |
|
|
|
= f (x) . |
то Ф (x) = f (x) , или |
( f (t)dt) |
|
|
a |
|
Теорема 2. Если |
F (x) есть некоторая первообразная от непрерывной |
|
функции f (x) , то справедлива формула
b
f (x)dx = F (b) F(a) .
a
Эта формула называется формулой Ньютона-Лейбница.
Разность первообразных функций обычно обозначают символом
b
F (b) F(a) = F (x) .
a
2
Пример 3. Вычислить интеграл sin xdx .
0

|
|
|
|
|
34 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. sin xdx = cos x |
|
|
= cos |
|
cos 0 =1. |
|
|
|
|
0 |
2 |
|
|
||||
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Замена переменных в определенном интеграле |
|
|
||||||
|
|
|
|
|
|
b |
|
|
Пусть необходимо вычислить интеграл |
f (x)dx , где |
f (x) |
непрерывная |
|||||
|
|
|
|
|
|
a |
|
|
на отрезке [a,b] функция. Положим x (t) , подчинив (t) |
условиям: |
|||||||
1. Функция (t) определена и непрерывна на отрезке [ , ] |
и ее значения |
|||||||
не выходят за границы [a,b] , т.е. если |
t [ , ], то a (t) |
b . |
||||||
2.( ) a , ( ) b .
3.На отрезке [ , ] существует непрерывная производная (t) .
Тогда имеет место формула
b |
|
|
|
f (x)dx = f ( (t)) (t)dt |
|
a |
|
Ввиду непрерывности подынтегральных функций существуют не только эти определенные интегралы, но и соответствующие первообразные. Замечание. Получив первообразную, выраженную через новую переменную t , к прежней переменной x не возвращаются.
2 |
|
|
Пример 4. Найти интеграл |
4 x 2 dx . |
|
0 |
|
|
Решение. Для вычисления интеграла воспользуемся подстановкой x 2sin t ,
тогда 4 x2 |
4 4sin 2 t 4cos2 t , |
dt 2cos tdt . Причем, |
если |
x 0 , |
t 0 , а если |
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
dx = 22 cos t2 cos tdt = 4 |
2cos 2 |
tdt = 4 2 |
1 |
|
||||
x 2 , |
t |
. Имеем: |
|
4 x 2 |
(1 cos 2t)dt = |
||||||||
|
2 |
||||||||||||
|
|
2 |
|
0 |
|
0 |
|
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
||||||
2(t 12 sin 2t)|0 2 = 2( 2 12 sin 0 12 sin 0) = .
3.2.Задания
Задача 1. Найти неопределенный интеграл
1. |
|
xdx |
|
. |
|
|
|
||
|
3 |
x2 2 |
||
2.x 2 dx .
x3 5
3.e x 
 2 5e x dx .
2 5e x dx .
4. |
e |
|
|
|
dx |
|
. |
|||||||
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
x |
|||||
5. |
|
|
arctgx |
dx . |
||||||||||
2 |
|
|||||||||||||
|
|
|
|
1 x |
||||||||||
6. |
|
sin(ln x) |
dx . |
|||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
x |
|||||||
7. |
|
|
|
|
e x |
dx . |
||||||||
1 |
2 x |
|||||||||||||
|
|
e |
||||||||||||

35
8. |
|
xdx |
|
. |
|
|
|
|
|
||
x |
2 |
|
5 |
||
|
|
|
|||
9.x 2 dx .
x6 5
10. |
|
|
x 2 dx |
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
6 |
|
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
11. |
|
|
|
|
xdx |
|
|
|
|
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
16 |
x |
4 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
12. |
|
|
2xdx |
|
|
|
|
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x |
2 |
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
13. |
|
ln 2 x |
dx . |
|
||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14. |
|
|
|
xdx |
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 x |
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
15. |
|
arcsin xdx |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
x |
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
16. |
|
|
|
cos xdx |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
sin |
2 |
x 1 |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
17.lnx5 x dx .
18.tgxdx .
19.tg 2 xdx .
20.
 1 cos 2 x sin 2xdx , использовать sin 2x 2sin x cos x .
1 cos 2 x sin 2xdx , использовать sin 2x 2sin x cos x .
21.sin 2 x cos xdx .
22.sindxx .
23.sin 3 xdx .
24.sin 2 x cos3 xdx .
25.ctgxdx .
26.cos7 xdx .
27.cos 4 xdx .
28.sin 4 xdx .
29.sin3 x cos 2 xdx .
30.ctg 2 xdx .
Задача 2. Найти неопределенный интеграл
1.arctgxdx .
2.(x 1)e2 x dx .
3.(3x 1) cos xdx .

36
4.(x3 x 1) ln xdx .
5.2ln xx dx .
xx dx .
6.x ln 2 xdx .
7.(x3 1) ln xdx .
8.(4x 3) cos(6x)dx .
9.(x2 1) ln xdx .
10.(x 5) cos(2x)dx .
11.(x 5) sin(3x)dx .
12.(4x 3)e3x dx .
13.(4x 3) sin(6x)dx .
14.ln(x2 1)dx .
15.x3 ln xdx .
16.(x 1) ln(x 1)dx .
17.xarctgxdx .
18.(x2 3x) ln xdx .
19.(2x 3)e2 x dx .
20.x sin(3x)dx .
21.x2 ln xdx .
22.ln(1 x)dx .
23.xe x 2 dx .
24.x2 cos xdx .
25.arctgxdx .
x
26. cos 2 x dx .
27. lnxx dx .
28. (x2 3x) ln xdx .
29. x2 e x dx .
30. xe5 x dx .
Задача 3. Найти неопределенный интеграл
1. |
|
|
dx |
. |
||
|
|
|
|
|||
x |
3 |
1 |
||||
|
|
|
|
|||
2. |
|
|
dx |
. |
||
|
|
|
|
|||
x |
3 |
8 |
||||
|
|
|
|
|||
37
3. |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x(x |
1) |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4. |
|
|
|
xdx |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
(x 1) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5. |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
5cos x |
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
6. |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(x |
2 |
1)(2 x) |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
7. |
|
|
|
(x2 |
2)dx |
. |
|
|
|
||||||||||||||||||||||
|
(x 1) |
2 |
(x |
1) |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
8. |
|
|
|
dx |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
9. |
|
|
|
|
dx |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x |
4 |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10. |
|
|
(x |
2 x)dx |
|
|
|
. |
|
|
|
|
|
||||||||||||||||||
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
6x 10 |
|
|
|
|
||||||||||||||||||||||
11. |
|
|
|
(3x2 8)dx |
|
|
. |
|
|||||||||||||||||||||||
|
x |
3 |
|
4x |
2 |
|
|
|
4x |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
12. |
|
|
|
(x3 1)dx |
|
|
|
|
|
. |
|
|
|
||||||||||||||||||
|
x |
3 |
|
5x |
2 |
|
|
|
|
6x |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
13. |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
sin x cos x |
|
|
|
|
|||||||||||||||||||||||||
14. |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
sin x 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
15. |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
cos x 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
16. |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
sin x cos x |
|
|
|
|
|||||||||||||||||||||||||
17. |
|
|
cos xdx |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
cos x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
18. |
|
|
sin xdx |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
sin x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
19. |
|
|
sin xdx |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
sin x 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
4sin x |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
8 |
7 cos x |
||||||||||||||||||||||||||||
21. |
sin(9x) sin xdx . |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
22. |
|
|
|
|
|
xdx |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
23. |
|
1 |
|
|
x 2 |
dx . |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
24. |
|
|
x 2 dx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
25. |
|
|
(3x 2)dx |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
x(x 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||

38
26. |
|
dx |
. |
|
|
|
|
||
x |
3 |
x |
||
|
|
|
||
2dx
27. (x 1)(x 2) .
3dx
28. (x 1)(x2 2) .
29. |
|
|
(x 3)dx |
. |
|||||
|
|
|
|
|
|
|
|||
|
x |
3 |
x |
2 |
|
2x |
|||
|
|
|
|
|
|||||
30. |
|
|
|
|
dx |
|
|
||
|
|
|
|
|
|
|
|
||
1 |
3sin x cos x |
||||||||
|
|||||||||
Задача 4. Вычислить определенный интеграл
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
x |
x2 16dx . |
|||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
dx . |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
3x |
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
4x |
2 |
|
|
|
|
|
|
|
|
||||
3. |
|
|
|
dx . |
|||||||||||||
|
|
|
|
|
|||||||||||||
|
1 |
|
|
2x 1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||
4. |
|
|
|
|
|
|
|
dx . |
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
|
4 |
|
|
|
x 1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
e2 |
2 ln x 1 |
|
|
|||||||||||||
5. |
|
dx . |
|||||||||||||||
|
|
|
|
||||||||||||||
|
e |
|
|
|
x |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
4 |
|
|
|
dx |
|
|
|
|
|
|
||||||
6. |
|
|
|
|
|
|
|
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
2x |
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1
7.x 2 
 1 x3 dx .
1 x3 dx .
2
ln 8 |
e |
x |
dx |
|
|
||
8. |
|
|
|
. |
|||
|
|
|
|
|
|
||
|
|
|
x |
||||
ln 3 |
1 e |
||||||
ln 2
9. xe x dx .
0
e
10. x ln xdx .
1 e
11. ln 2 xdx .
1

 3
3
12. arctgxdx .
0
1
13. x2 e x dx .
0
14. x 2 e x dx .
0
39
2
15.(x 3) sin xdx .
0
16. x sin x cos xdx .
2
17.cos3 x sin xdx .
0
7x5
18.7 x6 2 dx .
2
19.sin 3 xdx .
0
ln 2
20. 
 e x 1dx .
e x 1dx .
0
1dx
21.0 x2 4x 5 .
dx
22.0 3 2 cos x .
3dx
23.1 x
 x2 5x 1 .
x2 5x 1 .
1 |
|
|
|
|
24. 2 |
|
1 x |
dx . |
|
|
||||
0 |
|
1 x |
||
|
|
|
|
|
2dx
25.1 x 2 2x .
0dx
26.11 3  x 1 .
x 1 .
4
27.tg 3 xdx .
0
28.x2 
 9 x2 dx .
9 x2 dx .
3
29.2 3x4 5x2 7dx .
1x
2
30.x 2 cos xdx .
0
Задача 5. Найти площадь фигуры, ограниченной линиями
1.y ex , y e x 2 , y e2 .
2.y x4 2x2 , y 0.
3.y 3 2x x2 , y x 1.
4.y x2 3, xy 4, y 2, x 0.
40
5.y x3 , y 2x2 3x. (фигура расположена в первой четверти).
6.y 
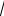 1 x, y x 1.
1 x, y x 1.
7.y cos 2x, y 0, x 0, x 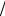 4 .
4 .
8.y 2 x4 , y x2 .
9.xy 1, y x2 , x 3, y 0 .
10.x 0, x 2, y 2x , y 2x x2 .
11.y arcsin 2x, x 0, y 2 .
12.y x2 1, x y2 ,3x 2y 16 0, x 0 .
13.y (x 1)2 , y 2 x 1 .
14.y 4 x2 , y x2 2x, y 0 (фигура расположена во второй четверти).
15.y 12 x2 2; x 2 y 4 0; y 0.
16.y x3 , y 4x.
17.y sin x, y 0 при 0 x .
18.y 4x , x 1, x 4, y 0.
19.y 12 x2 2x, y 0.
20.y x2 , xy 8, y 0, x 4.
21.x 
 y 1, x 0, y 5.
y 1, x 0, y 5.
22.y ln x, y 0, x e.
23.y x2 4, y x2 , x 0.
24.y 
 6x, y
6x, y 
 16 x2 , x 0.
16 x2 , x 0.
25.y x2 1, x y2 1, y 0, x 0, x 2.
26.x 0, y 4x x2
27.y x3 , y 0, x 4 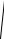 13 ..
13 ..
28.x2 y 2 9 при x 2;1 .
29.y 2
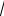 x, y 0, x 1
x, y 0, x 1
30.y e x , y 0, x 0, x 1.
Задача 6. Найти объемы тел, образованных при вращении вокруг оси Ox и оси Oy плоской фигуры, ограниченной линиями
1.y x3 , y 4x.
2.y sin x, y 0 при 0 x .
3.y 4x , x 1, x 4, y 0.
4.y 12 x2 2x, y 0.
5.y x2 , xy 8, y 0, x 4.
6.x 
 y 1, x 0, y 5.
y 1, x 0, y 5.
