13/Представление физ величин с помощью операторов.

Согласно принципу суппоз волновых ф-ции -описывает некоторое состояние системы.определяет вероятность значенияпри изменении физ величины, когда система нах в состоянии описываемом волновой ф-цией. Тогда среднее значениев данном состоянии описывается волновой ф-циейи равно сумме произведении собственных физических значенийна собственную вероятность. Определимсоответствующей данной физ величинеследующим образом – пусть- обозначает действия операторасоответствующие данной физ величине наф-цию, тогда интеграл от произведенияна комплексно сопряженноеесть среднее значение данного состояния..

Покажем что каждой величине в квантовой механике ставим в соответствие линейный оператор, для этого запишем среднее значение физической величины не через а через самуф-цию описывающую состояние системы. Любая волноваяф-ция удовлетворяет усл нормировки, кроме того. Поскольку из принципа суппоз имеемтодолжно быть билинейной по.

Следовательно мы можем приравнять .;, сравним с левой частью ур-ния (1).;и сравним с определением оператора соответствующем данной физ величине, т.е стаким образом получаем.

Если является одной из собственных ф-цииданной физ величины тогда все коэффициентыв сумме кроме 1-го равно нулю, этот =1, т.е. С учетом чтоподставим во 2-е ур-ние, т.о каждой физ величинеможно подставить в соответствие линейный оператор- это соответствует св-ву линейности оператора.

Собственные значения и собственные ф-ции линейных операторов.

Из ур-ния следует, что еслиявляется одной из собственных ф-циито получается, т.е действия операторанасводится к умножению собственных значений на собственную ф-цию. Поскольку согласно принципу суппозто- это ур-ние на собственные ф-ции и собственные значения. Решая это ур-ние мы находим- собственные ф-ции оператора. Но решения могу существовать при определенных значенияхназываемых собственными значениями оператора.

В квантовой механике считают что собственные ф-ции и собственные значения оператора данной физ величиныявляются собственными значениями и собственными ф-циями данной физ величины. Чтобы это показать получим что среднее значение физ величиныв данном состоянии имеет одно и тоже значение если это состояние описывается собственной волновой ф-цией, т.е

Предположим что в данных состояниях выполняется соотношение и подставим в ур-ние (2), получим, т.е среднее значение физической величины данного состояния = самому значению этой величины. Это возможно тогда когда результат каждого измерения равенотсюда следует что собственные значения и собств ф-ции оператора = -//- и -//- данной физ величины.

Ур-ние на собственные ф-ции и собственные значения оператора, решая это ур-ние мы находим собственные знач и -//- ф-ции данной физ величины, значит можем найти, которые определяют вер-ть данной физ величины и.

Условия возможности одновременного измерения различных физ величин.

Пусть и2 оператора каждому соответствует свои спектр собственных значений. Всегда ли существует состояниев котором оба оператора имеют определенное собственное значение, т.е одновременно измерены.

Допустим что явл собственной ф-цией оператораи одновременно -//-тогда ур-ния на собственные ф-ции и значения сводятся к умножению как длятак иЕсли система находится в состоянии описываемойто физ величиныиодновременны измеримы и собственные значения этих величиниданных состояний. Домножим 1-е ур-ние наполучим:. А теперь в обратную сторону:. Правые части равны однако нельзя сказать что, т.к это записано для единственногоа если все собственные ф-цииоператораявл собственными ф-циями операторато согласно принципу суппоз можно записатьЕсли 2 величины одновременно измеримы то их коммутатор = 0. Докажем и обратную теорему: Если коммутатор = 0, то эти 2 физ величины одновременно измеримы, т.о необходимым и достаточным условием для одновременно измеримых физ величин явл = 0 коммутатора.

Основные операторы квантовой механики.

1. Оператор координат есть сама координата . Ур-ние на собственные ф-ции и значения-- т.е этому удовлетворяет любая волновая ф-ция, тогда собственные значения координат принимают любые значения и спектр не прерывен.

2. Оператор проекции импульса имеет вид . Покажем что это так для частицы движущейся в волновом пр-ве. Посмотрим удовлетворяет ли вид оператораур-нию на собственные ф-ции и собственные значения., т.о оператор проекции импульса удовлетворяет ур-нию на собственные ф-ции и значения, т.е,,.

3. Оператор полного импульса. В классической механике в квантовой мех;. Проверим является ли координатаи проекцияодновременно измеряемыми величинами.

;;, значит. Одновременно измеритьинельзя это согласуется с соотношением неопределенности Гейзенберга. Аналогично дляи.; Коммутатор равен 0 значит можно одновременно измеритьи.

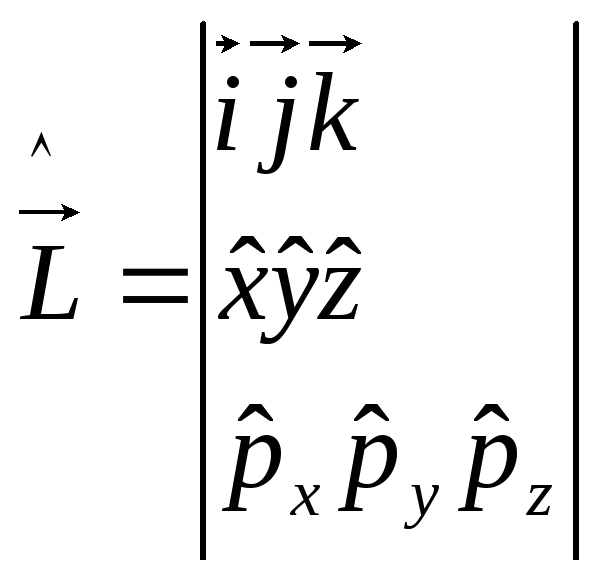4. Оператор момента импульса. В классической механике . В квантовой те же соотношения только между операторами,, т.е, т.е,,Определим можно ли одновременно измерить все 3 проекции импульса или 2.;.

. Вычитаем, т.о осталось,,, т.о их коммутаторы отличны от нуля а это значит что одновременно измерить 2 проекции момента импульса невозможно, значит оператор момента импульса не имеет собственных значений и собственных ф-ций.

Т.е нельзя одновременно определить и величину момента импульса и направления. Возникает вопрос можно ли измерить хотя бы 1 проекцию импульса если 1 можно измерить то из этого следует что все 3 проекции имеют определенные значения но не могут одновременно быть измерены.

Перейдем в сферическую систему координат.

В сферической системе координат операторы проекции импульса имеют сложный вид А. Запишем ур-ние на собственные ф-ции и собственные значения для операторапоскольку он простой:,;;;.

Волновая ф-ция должна быть непрерывной, поэтому при изменении наволновая ф-ция должна сохраняться, т.е,экспоненциальная ф-ция периодична с периодом.

Пр:;,.-магнитное квантовое число, определяет проекцию момента импульса на заданное направление (осьz). Т.о одна проекция импульса принимает определенное значение, но одновременно все 3 не могут. Другой величиной характеризующей момент импульса является квадрат модуля момента импульса. Можно показать что коммутатор модуля равен 0., т.е можно одновременно измерить проекцию момента импульса по заданному направлению и квадрат момента импульса. Ур-ние собственной ф-ции и собственного значения- это ур-ние имеет решение при,- орбитальное квантовое число, определяет квадрат момента импульса или модуль момента импульса:. Поскольку проекция момента импульса, то. Максимальное значение, которое оно может принимать, т.о,…всего. (рис.).может иметь только определенное направление, так что проекция момента импульса имеет значения

5. Оператор потенциальной энергии.

Если потенциальная ф-ция зависит только от координат потенциальной энергии, то, ур-ние собственной ф-ции и собственного значения

6. Оператор кинетической энергии.

В классической механике . В квантовой механике выполняются все теже соотношения,;, так же с; Т.о,;- оператор Лапласа.

7. Оператор полной энергии Д Альтониом.

В классической механике полная энергия . Еслизависит еще и отто в классической механике вводят ф-цию Гамильтона, определение полной энергии,.

8. Ур-ние Шредингера в операторной форме.

.. В стационарном состоянии. Тогда ур-ние Ш в стационарном состоянии;, тогда для стационарных состояний- ур-ние собственных ф-ции и собственных значений . Решая это находим собственные значения и собственные ф-ции энергии.

Связь квантовой и классической механик.

Теорема Эренфеста.

В квантовой мех между физ величинами выполняются теже соотношения что и в классич механике, только между операторами. Например: - кл мех,-квант мех. (1). Суть теории Эренхерста заключается в том что в квантовой механике выполняются теже самые соотношения но для средних значений.

,,. Если выполняется (1) то домножим слева наф-цию и получим,.

Принцип причинности квантовой механики.

В класс мех в каждый момент времени известно положение частицы и импульс. Зная координату и импульс частицы в нач момент времени и зная силы действующие на частицу, можно определить координату и импульс частицы в другой момент времени.

В квантовой мех одновременно измерить координату и импульс частицы нельзя. Состояние частицы описывается ф-цией аопределяет вероятность нахождения частицы, частица как бы размазана по пространству, поэтому кажется что в любой момент времени мы не сможем определить положение частицы и принцип причинности не работает.

Волновая ф-ция удов ур-нию Шредингера в которую входит первая производная, т.е зная волновую ф-цию в начальный момент времени мы можем определить волновую ф-цию в любой другой момент временимы можем определить вероятность нахождения частицы, т.е принцип причинности в кв мех изменяется- причина, а- следствие.

14\Применение квантовой механики.

Движение свободной частицы.

Свободная частица – частица которая движется в постоянном потенциальном поле. Для простоты будем считать что . Пусть частица движется вдоль оси Х. Ур-ние Шредингера,;; Обозначим;. Ищем решение ур-ния в виде.;;- хар. ур.,,;- решение собственной волновой ф-ции, распространение вдоль оси Х,реш собственной волн ф-ции Д’Броля, распространение против Ох. Решением явл полное решение,, т.е с равной вероятностью частицу можно найти в любой точке пр-ва.,. Ограничения нане накладываем.- может иметь любое значение, т.е энергетический спектр непрерывен.

15\ Движение частицы в одномерном потенциальном ящике с бесконечно высокими стенками.

График зависимости (рис.).

Ур-ние Шредингера.,(Здесь).Обозначим.. Ищем решение в виде.- хар. ур.;. Подставим в ур-ние Шредингера:,,. Комплексное число = 0 , тогда действительная и мнимая части =0. Тогда общее решение ур-ния Ш.;,. Т.о решение ур-ния Шредингера уже не явл комплексным а явл действительным. Граничные усл: волновая ф-ция – непрерывна поэтомуи. 1.Поскольку частица за пределы потенциальной ямы выйти не может поэтому.. А с другой стороны,. 2.-е граничное усл,,,. Если, то, частицы в ящике нет.,,;;не может быть поскольку в этом случае, т.е частицы в ящике нет.. Приравниваем. Граничные усл приводят к тому чтопринимает дискретные значения, при чем, т.е минимальное значение которое будет принимать энергия. Коэффициентнайден из усл нормировки.;,,,;.

,.

Графики для и.

Если частица имеет энергию то наиболее вероятное место ее нахождения этои. У границы ямы и в серии она не находится. Расстояние при 2-х энергетических уровнях, т.е с увеличением- расстояние увеличивается. Отношение расстояний между уровнями:. Еслимало тосравнимо с(). Есливелико то.

16\ Отражение и прохождение частицы сквозь потенциальный барьер бесконечной ширины.

(график). Для классической частицы существуют 2 случая: 1)(1)поэтому(2), т.е частица проходит во 2-ю область но движется с наименьшей скоростью.

2) в этом случае частица отражается от потенциального барьера, т.к, что недопустимо.

Для квантовой частицы. Запишем ур-ние Шредингера,

(1) ,;

(2) ,;(). Обозначим,. (1)(2). Волновая ф-ция и ее 1-я производная непрерывны поэтому в (1) обл должна существовать отраженная волна а во второй прошедшая, т.е в 1-ой есть прямая и отраженная а во 2-ой прошедшая, т.к отражаться не от чего, поэтому реш ур-ние Ш для (1)(2)(- прямая волнаотраженная). Коэффициент вф-ях можно найти из граничных условий. Волн ф-я определяется с точностью до постоянного множителя, поэтому можно перенормировать волн ф-цию (разделить выражения на) или сделать, чтоб не переобозначивать коэффициенты.

Граничные условия:

Волновая ф-ция и ее производная непрерывны на границе. Решение для ур-ния Ш,,,.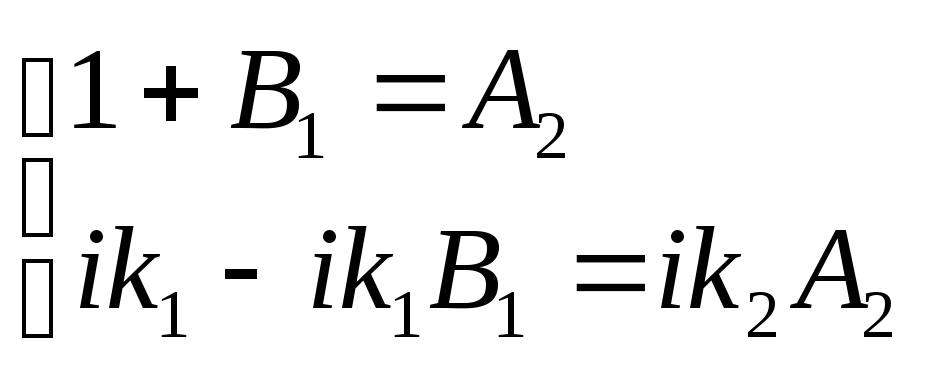

Коэффициент отражения назыв отношение плотности потока отраженных частиц к -//- падающих -//-. Коэффициент пропусканияназыв отношение плотности потока прошедших частиц к -//- падающих -//-. Покажем что,,, тогда;.

Закон сохранения числа частиц.

В квант мех это отражает то что вер-ть того что частица пройдет и отразиться =1.

Анализ поведения частицы в зависимости от соотношения междуи, 1),-действительное число,- длина волны Бролля.,следовательно. (графики)

2) ,,, где, тогда ур-ние Ш(график)

Коэффициент отражения ,,значит, т.е происходит полное отражение но волновая ф-я,значит существует вер-ть того что частица проникла во 2-ю область. Это противоречие разрешается тем что наше решение относится к стационарному состоянию, т.к оно основано на ур-нии Ш для стац состояний. Проникновение волны во 2-ю область происходит в переходный период когда состояние во времени еще не установилось. Исследование переходного периода может быть осуществлено на основе общего ур-ия Ш для не стационарных состояний. В найденном нами решении для стац сост состояние частицы описывается 3-мя волновыми ф-ями,,, т.е частица не локализована, она может находиться в любой т-ке пр-ва с любой вер-тью. Общим для всего этого состояния явл единый параметр это полная энергия частицы, т.о при- класс частица пройдет в обл потенциального барьера, но будет двигаться с меньшей скоростью. Квантовая частица имеет не нулевую вер-ть отразиться от потенциального барьера . При, кл частица обязательно отразиться от потенц барьера. Кв частица имеет не 0 вер-ть проникнуть в обл потенц барьера.

Над барьерное отражение и под барьерное прохождение частицы в обл потенциального барьера явл чисто квантовым эффектом.

17\Потенциальный барьер конечной ширины. Туннельный эффект.

(график) . Для классической частицы существуют 2 случая: 1)(1) и (3) обапоэтому,(2), т.е частица проходя над барьером уменьшает свою скорость.

2) в этом случае частица отражается от потенциального барьера, т.к ее кинетическая энергия будет (-), что недопустимо.

Для квантовой частицы. Запишем ур-ние Шредингера,

(1) ,;(3),;

(2) ,;(). Обозначим,. (1)(2),(3). Ур-ния Ш. Перенормируем.

Граничные условия:

Волновая ф-ция и ее производная непрерывны на границе. Решение для ур-ния Ш, для решения (1)*и + со (2).; (3)*и + затем - с (4).,.

Выражаем,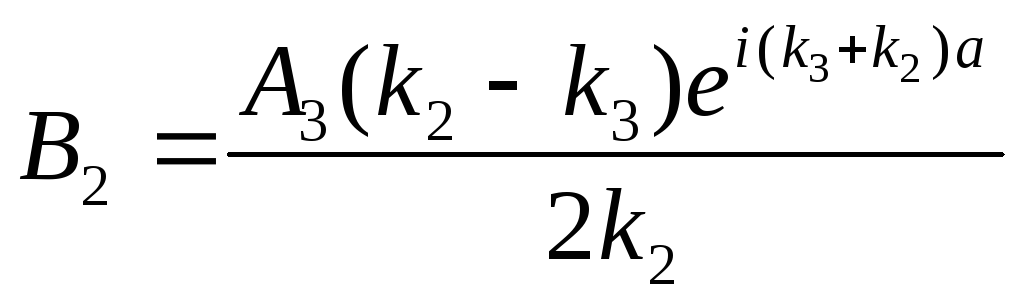. Подставим в 1-е ур-ние учитывая что,. Выразим,.

Поведение частицы в зависимости взаимоотношений и. 1),-действительное число,- длина волны Бролля.,следовательно. (графики)

2) ,,, где, тогда ур-ние Ш. Определение соотношения междуи,, т.е, поэтому(график). Есть вер-ть у частицы проникнуть через потенц барьер и попасть в обл 3. Определение коэффициента пропускания есть отношение плотности потока прошедших частиц к -//- падающим...;,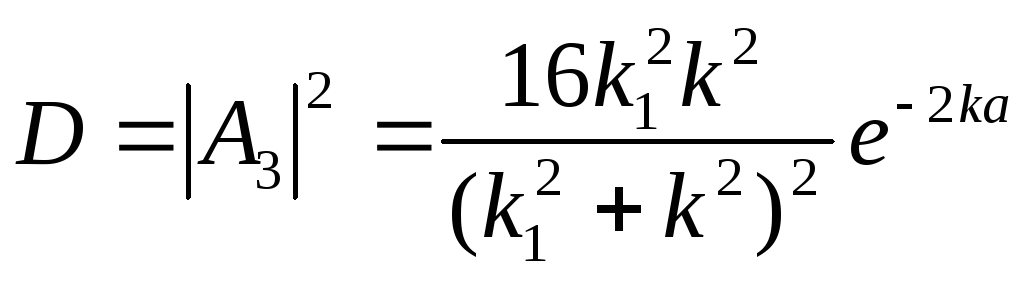. Покажем что коэффициент перед экспонентой слабо-меняющаяся ф-ция.;,тогда,, т.е сама ф-ция изменяется в малых пределах от 0 до 4-х. поэтому,. Если потенциальный барьер имеет сложную ф-лу то его можно разбить на бесконечно малые барьеры. Т.о прикл частица проходя над барьером уменьшает свою скорость, а квантовая частица имеет не нулевую вер-ть отразиться от каждой стенки потенциального барьера . При, кл частица обязательно отразиться от 1 стороны потенц барьера. Кв частица имеет не 0 вер-ть пройти сквозь потенц барьеры и появиться в 3 обл. (это туннельный эффект).

18\Потенциальная яма со стенами конечной высоты.

(рис.) . Запишем ур-ние Шредингера,

(1) ,;(3);

(2) ,. Обозначим,. (1)(2), (3). Волновая ф-ция непрерывна поэтому в (1) и (2) обл существуют прямая и отраженная волна а в (3) только прямая. Ур-ния Ш. Рассмотрим случаи 1),-действительное число,- длина волны Бролля.,следовательно. (графики)

2) ,,, где, тогда ур-ние Ш для (1). Волновая ф-ция должна быть ограниченной поэтому проверим: при,это не удовлетворяет условию ограниченности ф-ции поэтому. При,это удовлетворяет : при. Для (3). При,это удовлетворяет условию ограниченности ,. Для (2),здесь возникает стоячая волнакак и в случае потенциальной ямы с бесконечно высокими стенками решение можно представить в виде действительного числа:- преобразуем домножив на:,где,,переобозначим. Т.о решение ур-ния Ш имеет вид:(рис.)

Коэффициенты можно найти из граничных условий: Волновая ф-ция и ее производная непрерывны на границе. Решение для ур-ния Шдля решения (2):(1) и (4):(3) получили:;итого;. Сделаем чтоб окончательное ур-ние было выражено только черездля этого;;, поэтому, т.о. Из второгоили., тогда- это ур-ние имеет корни и находя их мы найдем корни энергии.,. Видно чтоимеет дискретные значения поэтому иимеет дискретные значения, причем. В случае потенциальной ямы с бесконечно высокими стенками энергетический спектр дискретен но число уровней бесконечно. В случае потенциальной ямы конечной глубины – энергетический спектр дискретен но количество уровней энергии конечно и определяется числом решений ур-ния (5).

Если , то ограничений нанет поэтому энергетический спектр непрерывен.

19\Гармонический осциллятор.

Это система которая совершает колебания под действием квазиупругой силы ., тогда,. Потенциальная энергия гармонического осциллятора, поэтому оператор Домельтониана;. Ур-ния на собственные ф-ции и собственные значения. Подставим(1) Ур-ние Ш для гармон осцилл. Преобазуем (1) умножив обе части ур-ния наи получили:. Введем безразмерные параметры:,,. Продифференцируем (1) пополучим:;. Поставим во (2) ур-ние, т.о. При определенных значенияхэто ур-ние имеет решение в виде, поставими. Подставим в ур-ние (3)и получили: ,. Э то ур-ние имеет решение для всех,и.

Проверим: должна быть ограниченаприне удовлетворяет условию.приудов условию тогда.и. Энергия основного состояния,. Для остальных значений энергии в стационарных состояний решение ур Ш можно представить в виде.- полиномn-ой степени. Подставим это в;.;.подчеркнуты полиномыn–ой степени. Еслипри слагаемомстоит коэффициент, то в, пристоит коэффициентприравняем коэффициент при одинаковых степенях полинома получаем;. Подставляяв (4) получим;. Полиномы являются решением ур-ния (5) и называются полиномы Чербышева. Подставимв (4).- значение энергии в гармоническом осциллятора, где- энергия нулевых колебаний. Волновое ур-ние. Полином Чербушева Эрминаявляется решение ур-ния (5).(рис.) параболическая потенциальная яма.. В квантовой механике доказано что переход из одного состояния в другое возможен только если, т.е при переходе из одного состояния в другое возможно испускание или поглощение,, т.к разность между энергетическими уровнями одинакова.

Условия накладывающиеся на квантовые числа при переходе из одного состояния в другое называются правила отбора. Испускание или поглощение с, согласуется с гипотезой Планка о том что испускание тел происходит квантами, но Планк это постулировал и мы получили это при решении ур-ния Ш, так же при решение ур-ния Ш появилась энергия нулевых колебанийэто подтверждается опытом.

20\Ур-ние Ш для атома водорода (Н).

В классическом понимании (Н) представляет протон вокруг которого движется . Потенциальная энергия:, при,и при,. (график рафик.) Посколькуневозможно, тодвижется в гиперболической потенциальной яме.

Ур-ние Ш для стационарных состояний.

;;.

перейдем в сферическую систему координат. (рис.);. Оператор квадрата момента импульса:, тогда.,;, где 1-ое слагаемое зависит только от(описывает радиальное движение) 2-ое зависит оти описывает кинетическую энергиюв поле ядра, т.о ур Ш для водородоподобного атома имеет вид:или же. Решение ур Ш можно представить в видеКакова бы не была бы зависимостьф-ции, для состояний с определенным значением квадрата момента импульса выполняются ур-я на собственные ф-ции и собственные значения :- это ур-ние имеет решение при,-главное квантовое число. Из ур Ш следует что при данном,принимает значения.следовательно что коммутатор =0,т.е, т.кдействует только на, атолько на, кроме того, т.кдействует только на, атолько на. Т.е,иопределенное значение могут принимать одновременно,где- проекция момента импульса.- определяется орбитальным квантовым числом,- энергия определяется главным квантовым числом.

,где- магнитное квантовое число определяет проекцию момента импульса на заданное направление, т.о состояниев атоме определяется квантовыми числами,,. Определенному значению энергии соответствует несколько состояний отличающихся квантовыми числами,. Такое состояние называют вырожденным. Степень вырождения это число состояний соответствующее данному значению энергии посчитанному дляв атоме водорода. При данном,принимает значения, всегозначений, при данном,, всего. Степень вырождения:, состояниеопределяетсяф-цией но она не имеет физ смысла,имеет физ смысл, т.еразмазан в пр-ве и числами,определяем форму и размер электронного облака, аориентацию. Состояние сназываетсясостоянием; состояние сназывается; сназывается; сназывается. Например:означает. (рис.) длягде жирнее там вероятнее. Длярассмотрим(рис.)

В квантовой механике доказано что переход из одного состояния в другое осуществляется если выполняется условие: ,т.е они при переходе изменяются.

Энергетический спектр (рис.) Переход на 1-ый ур, т.е на соответствует серии Лаймона,- Серия Бальмера.

Состояние в атоме водорода.

Наидем решение ур Ш для атома водорода в состоянии :.состояние:, тогда ур Ш имеет видищем решение ур Ш в видетогда,Подставим в ур Ш:;- Это ур-ние имеет решение при всех значенияхтогда содержимое скобок =0, т.е;. Это решение ур Ш- первый боровскии радиус,- из усл нормировки;.;.сопоставимитого, т.е, т.о состояниеописывается волновой ф-циейи энергией- Вероятность нахождения частицы в эл-те объемаравна,- плотность вероятности.. Проанализируемдля этого, т.есоответствует-min,соответствует-min,соответ-max. (рис.) В теории Борадвижется по орбитали припо 1-ой Боровской орбите. Здесьимеет наиболее вероятное положение.

21\Магнитные моменты атомов. Опыты Штенра и Герлаха. Спин электрона. Спиновое квантовое число. Спин-орбитальное взаимодействие.

В класич механ двигаясь по круговой орбите вокруг ядра обладает моментом импульса и магнитным моментом связь между этими величинами в классич мех переносится в квант мех но меж соответствующими операторами.

Рассмотрим движущийся вокруг ядра (рис.),. Движущемусявокруг ядра можно сопоставить ток- ток направлен в обратную сторону от движения. Магнитный моментгдезначит. Связь междуи:;- гиромагнитное отношение, т.е;.Запишем для операторов в кван мех теже соотношения:,- не имеет собственного значения. Определенные значения имеет, т.е, а значит определенные значения имеет модуль,,и- магнитон Бора.. Определенные значения принимает проекция момента импульса на заданное направление,;, т.о орбитальный магнитный момент квантуется и- при данном,.

Опыты Штенра и Герлаха.

Узкий пучок атомов водорода или серебра проходил через сильно неоднородное поле и попадал на фотопластину оставляя на ней следы, оказалось что после прохождения поля пучок раздваивается. (рис.) Если атомы водорода находятся в основном состоянии, т.е тои проекция момента импульса на заданное направление, т.е магнитное поле не должно оказывать влияние на атом и пучок должен пройти спокойно. Если (Н) находится не в основном состоянии тоизначит в силу неоднородности – магнитного поля на атом действует сила равная, т.е при данном, т.е всегозначений – это значит что пучок должен расщепиться на нечетное число пучков что не согласуется с экспериментом. С точки зрения класс мех- принимает произвольное значение поэтому при прохождений через неоднородное поле пучок должен уширяться! Этот эксперимент позволил предположить Гаутсмиту чтообладает собственным неуничтожимым магнитным моментом называемый спином . Предполагалось в начале что наличие спина обуславливается движениемвокруг собственной оси. Гиромагнитное отношение для,. Получим все из ур Дирака – для релятивистской кван мех. Т.е спин такая же хар-какаки- масса и заряд. Спин – это и релятивистский и квантовый эффект. Спину нет аналога в классической механике.

Орбитальный момент импульса - ;,всего.

Спиновой момент импульса - ;,;;всего.;;всего.

Опыт Штерна и Герлаха показывает что после прохождения магнитного поля расщепляется на 2 уровня. .

Орбитальный момент импульса и спиновой м и складываются по правилу векторной суммы. ,,;,.

Со спином связан магнитный момент наличие орбит м м и спинового м м приводят ко взаимодействию этих магнитных моментов точно так же как взаимодействуют магниты или токи – это спин-орбитальное взаимодействие, оно зависит от взаимной ориентации орбитального м м и спинового м м. Если атом находится в состоянии с определенным значением ,то осьдля спинового м м совпадает с осьювыбранной для орбитального м м. Спиновой м м имеет всего 2 проекции вдоль и против оси, т.е вдоль и против орбитального м м. Если спинов м м совпадает с направлением орбит м м то потенциальная энергия системы уменьшается, а если в противоположную сторону то увеличивается. В результате энергия уровней расщепляется на 2 подуровня. Совокупность подуровней на которые расщепляется данный уровень называется мультиплет, т.е при данномвозможно всегосостояний. Рассмотримв этом случаеэтосостояние и записывается оно- этот уровень не расщепим т.к орбит м исоответственно орбит м м- такой не расщепимый уровень называется симплет.

Рассмотрим ,, т.еизначит возникает спинно-орбитальное взаимодействие (рис.). Правило отбора:из-за спинно-орбитального взаимодействия происходит расщепление уровней которое приводит к расщеплению спектральной линии. Это называется тонкой структурой а уровень назыв дуплетным.

Эффект Зеемана.

Эффект Зеемана – это расщепление энергетического уров и спектральной линии при помещении атома в магнитное поле. в атоме обладает магн моментами – спиновым и орбитальным. Рассматриваем только орбит м м.(рис.) тогда элемент работыотсюдаи- эта работа идет на изменение потенциальной энергии – энергия,.или, знакпоказывает что при,.проекция..

Правило квантования: ,значит, т.о к энергии которой обладаетв отсутствии магнитного поля прибавляется энергия в магнитном поле, значит при,;,еслитоне происходит расщепления в поле а длясостояния, значит взаимодействия с магнитным полем нету. Еслитогда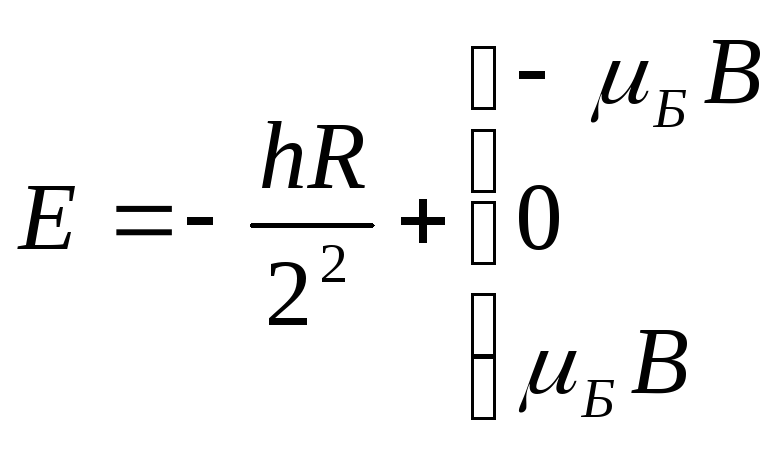энергетич уровень расщепляется на 3. И т.д и т.п. Расстояние между 2-мя расщепленными уров равняется(рис прии при) в них переходы возможны когдаи, тогда, а,, т.е. Величина расщепления зависит от величины магнитного поля. За счет того что происходит Зееманово расщепление происходит и расщепл спектральных линии.

Рассмотрим случаи. Переход с на(мега рисунки.) Расстояние меж уровнями одинаковы,тута на рисунке переходы возможны не все. Получили 9-ть переходов но расстояние между соседними уров одинаковы поэтому получилось 3 перехода.