Краткий курс математического анализа. Том 1

178 Гл. 1. Дифференциальное исчисление функций одной переменной

определенного знака бесконечную производную, то существует такая точка ξ (a, b), что

Это равенство называется формулой конечных приращений Лагранжа.

Рассмотрим вспомогательную функцию

где λ — некоторое число. Эта функция непрерывна на отрезке [a, b] и в каждой точке интервала (a, b) имеет конечную или определенного знака бесконечную производную (см. замечание 4). Подберем число λ так, чтобы выполнялось соотношение

тогда функция F будет удовлетворять всем условиям теоремы Ролля. Из условий (12.6) и (12.7) имеем равенство f (a) − λ(a) = f (b) − λb,

При этом λ, согласно теореме Ролля, существует такая точка ξ (a, b),

= f (x) − λ, то из (12.8) и (12.9) получаем

f (ξ) − f (b) − f (a) = 0, b − a

что равносильно равенству (12.5).

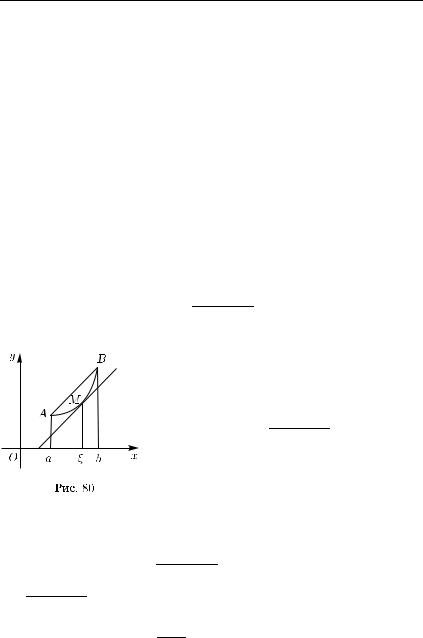
Геометрический смысл теоремы Лагран-

жа состоит в том, что на дуге AB (рис. 80) графика функции f с концами в точках

A = (a, f (a)) и B = (b, f (b)) найдется точка M = (ξ, f (ξ)), касательная в которой параллельна хорде AB. Действительно, согласно теореме Лагранжа

и ξ = a + θ(b − a). Поэтому формулу Лагранжа можно также записать в виде

Заметим, что равенство (12.10) остается верным и при b < a (а поэтому и равенство (12.11) при x < 0), так как при перемене местами a и b его левая часть не меняет знака, причем в этом случае также

ξ= a + θ(b − a), 0 < θ < 1 (здесь b − a < 0, ξ − a < 0).

Сл е д с т в и е 1. Если функция непрерывна и имеет производную, равную нулю, во всех точках некоторого промежутка (конечного или бесконечного), то она на нем постоянна.

Действительно, пусть функция f удовлетворяет сформулированным условиям на некотором промежутке и x1, x2 — две произвольные его точки, x1 < x2. Тогда функция f непрерывна и дифференцируема на отрезке [x1, x2] (на концах этого отрезка в смысле соответственно односторонней непрерывности и односторонних производных). По теореме Лагранжа

Во всех точках промежутка, на котором рассматривается функция f , по условию f (x) = 0, в частности f (ξ) = 0. Поэтому из равенства (12.12) следует, что f (x1) = f (x2).

Поскольку x1 и x2 — произвольные точки указанного промежутка, то это и означает, что функция f на нем постоянна.

В частности, производная не может иметь устранимую точку раз-

180 Гл. 1. Дифференциальное исчисление функций одной переменной

Из этого равенства следует, что левая часть равенства (12.13) имеет конечный или бесконечный предел, т. е. существует конечная или бесконечная производная f (x0), причем

Утверждение, аналогичное следствию 2, имеет место и для односторонних производных.

З а м е ч а н и е 5. Из следствия 2 вытекает, что если функция f непрерывна на некотором промежутке (конечном или бесконечном) и имеет производную, равную нулю во всех точках этого промежутка, кроме, быть может, конечного множества его точек, то функция f постоянна на указанном промежутке.

Действительно, в этом случае в достаточно малых проколотых окрестностях точек рассматриваемого конечного множества производная функции равна нулю и, следовательно, имеет в этих точках предел, равный нулю по проколотым окрестностям. Согласно следствию 2 в указанных точках также существует производная и она рав-

на нулю. Поэтому в силу следствия 1 функция является постоянной. Те о р е м а 4 (Коши). Если функции f и g:

1)непрерывны на отрезке [a, b];

2)дифференцируемы в каждой точке интервала (a, b);

3)g (x) = 0 во всех точках x (a, b);

то существует такая точка ξ (a, b), что

Прежде всего заметим, что для функции g справедливо неравен-

так как если бы имело место равенство g(a) = g(b), то в силу теоремы Ролля нашлась бы такая точка x0 (a, b), что g (x0) = 0, а это противоречило бы условиям теоремы. В силу неравенства (12.16) левая часть формулы (12.15) имеет смысл.

Рассмотрим теперь функцию

где число λ подберем таким образом, чтобы имело место равенство

Тогда функция F будет удовлетворять на отрезке [a, b] условиям теоремы Ролля. Из соотношений (12.17) и (12.18) имеем

f (a) − λg(a) = f (b) − λg(b),

182 Гл. 1. Дифференциальное исчисление функций одной переменной

Доопределим функции f и g в точке x = a по непрерывности, т. е.

Тогда для любого x (a, b) продолженные функции на отрезке [a, x] будут удовлетворять условиям теоремы Коши о среднем значении, и потому будет существовать такая точка ξ = ξ(x), a < ξ < x, что

13.2. Неопределенности вида ∞∞ .

Те о р е м а 3. Если:

1)функции f и g дифференцируемы на интервале (a, b);

2)g (x) = 0 для всех x (a, b);

Если a < x < x0 < b, то на отрезке [x, x0] функции f и g удовлетворяют условиям теоремы Коши (см. теорему 4 в п. 12.2), а поэтому существует такая точка ξ = ξ(x0, x), что

в силу условия (13.7) стремится к 1 при x → a и фиксированном x0:

Непосредственно перейти к пределу в равенстве (13.12) нельзя, так как указанные выше предельные переходы в сомножителях в правой части равенства происходят при разных условиях: при x0 → a и при фиксированном x0, но x → a. Однако если задать произвольно окрестность U (k) предела k отношения производных (13.9), то можно сна-

чала зафиксировать точку x0 столь близко к точке a, что отношение f (ξ)

g (ξ) попадет в эту окрестность, ибо a < ξ < x0. Согласно же условию

(13.13) для всех точек x, достаточно близких к a, отношение f (x) g(x)

184 Гл. 1. Дифференциальное исчисление функций одной переменной

(см. (13.12)) также будет принадлежать указанной окрестности U (k), а это означает справедливость утверждения (13.10).

Проведенное рассуждение нетрудно записать с помощью неравенств.

Пусть сначала предел (13.9) конечный. Положим

Тогда из (13.9) будем иметь lim α(x) = 0, и, следовательно, для лю-

x→a

бого произвольно фиксированного ε > 0 существует такое x0, что для всех x (a, x0) выполняется неравенство

В результате получаем, что для всех x (a, a + δ) выполняется неравенство