
Краткий курс математического анализа. Том 1
.pdf§ 4. Числовые множества |
67 |
а если λ < 0, то |
(4.12) |
sup λX = λ inf X, |
|
inf λX = λ sup X. |
(4.13) |
Пусть λ > 0. Если y λX, т. е. y = λx, где x X и, следовательно, x sup X, то y = λx λ sup X. Если y < λ sup X, т. е. y/λ < sup X,
то найдется такое x X, что x > y/λ и, следовательно, λx > y, где λx λX. Таким образом, λ sup X является верхней гранью множества λX, т. е. формула (4.11) доказана. Аналогично доказывается и формула (4.12).
Пусть теперь λ < 0. Если y λX, т. е. y = λx, где x X и, следовательно, x inf X, то λx λ inf X. Если y < λ inf X, т. е. y/λ > inf X, то
найдется такое x X, что x < y/λ, а потому λx > y, где λx λX. Это и означает, что λ inf X является верхней гранью множества λX. Равенство (4.13) доказано. Аналогично доказывается равенство (4.14).
Положим теперь для каждого множества X
def |
(4.14) |
−X = (−1)X. |
|
Очевидно, что из определения суммы X + Y и разности X − Y мно- |
|
жеств следует |
(4.15) |
X − Y = X + (−Y ). |
|
В силу определения (4.15) из второго свойства при λ = −1 полу-
чаем |
inf (−X) = − sup X. |
(4.16) |
sup (−X) = − inf X, |
||
3◦. |
|
(4.17) |
sup (X − Y ) = sup X − inf Y. |
||
Следует сразу из первого свойства и формул (4.16) и (4.17).
4.4. Принцип Архимеда.
Те о р е м а 2. Каково бы ни было действительное число a, существует такое натуральное число n, что n > a.
Если бы утверждение теоремы не имело места, то нашлось бы такое число a, что для всех натуральных чисел n выполнялось бы неравенство n a, т. е. множество натуральных чисел N было бы ограничено сверху. Тогда, согласно теореме 1, у множества N существовала бы конечная верхняя грань:
β = sup N < +∞. |
(4.19) |
Поскольку β − 1 < β, то в силу определения верхней грани (см. свой-
ство 2 в определении 2 в п. 4.2) найдется такое натуральное число n,
что n > β − 1, т. е.
n + 1 > β, (4.20)
но n + 1 — также натуральное число: n + 1 N, поэтому неравенство (4.20) противоречит условию (4.19).
3*
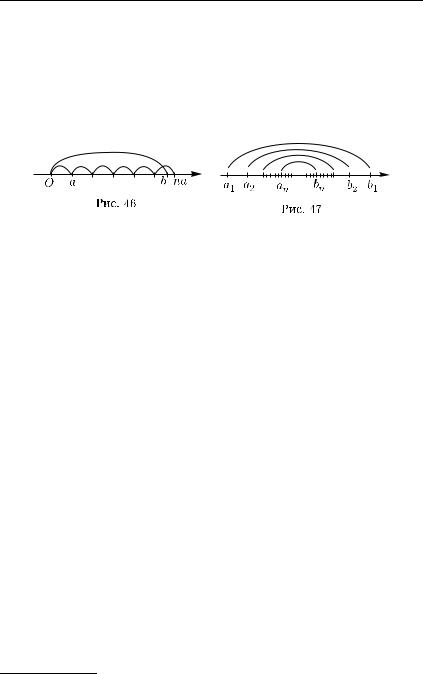
68Гл. 1. Дифференциальное исчисление функций одной переменной
Сл е д с т в и е (принцип Архимеда 1)). Для любых чисел a и b таких, что 0 < a < b, существует натуральное число n, для которого выполняется неравенство (рис. 46)
na > b. |
(4.21) |
Действительно, согласно теореме 2 для числа b/a существует такое натуральное число n, что n > b/a, откуда сразу и следует (4.21).
4.5. Принцип вложенных отрезков.
О п р е д е л е н и е 3. Система числовых отрезков
[a1, b1], |
[a2, b2], ..., [an, bn], ..., an R, bn R, n = 1, 2, ..., |
(4.22) |
называется системой вложенных отрезков, если |
|
|
|
a1 a2 ... an ... bn ... b2 b1, |
(4.23) |
т. е. если |
(рис. 47) |
|
|
[a1, b1] [a2, b2] ... [an, bn] ... |
|
Те о р е м а 3. Всякая система вложенных числовых отрезков имеет непустое пересечение.
Пусть задана система вложенных отрезков (4.22). Обозначим через A множество всех левых концов an отрезков этой системы, а через B — множество их правых концов bn. Из неравенств (4.23) следует, что для любых номеров m и n выполняется неравенство am bn. Поэтому по свойству непрерывности действительных чисел (п. 2.1, свойство V) существует такое число ξ, что для всех номеров m и n выполняется неравенство
am ξ bn,
в частности, неравенство an ξ bn, n = 1, 2, ... Это и означает, что точка ξ принадлежит всем отрезкам [an, bn].
Укажем условие, при котором пересечение системы вложенных отрезков состоит из единственной точки.
1) Архимед (287–212 до н.э.) — древнегреческий математик и механик.
§ 4. Числовые множества |
69 |
О п р е д е л е н и е 4. Длины bn − an отрезков [an, bn], an R, bn R, an bn, n = 1, 2, ..., называются стремящимися к нулю, если для
любого числа ε > 0 существует такой номер nε, что для всех номеров
n > nε выполняется неравенство |
|
bn − an < ε. |
(4.24) |
Те о р е м а 4. Для всякой системы вложенных отрезков |
[an, bn], |
n = 1, 2, ..., длины которых стремятся к нулю, существует единственная точка ξ, принадлежащая всем отрезкам данной системы; при этом
Если точки ξ и η принадлежат всем отрезкам рассматриваемой системы, т. е.
ξ [an, bn], η [an, bn], n = 1, 2, ...,
то ясно, что для всех номеров n выполняются неравенства
|η − ξ| bn − an,
а следовательно, в силу условия (4.24) для любого ε > 0 справедливо
неравенство |
(4.26) |
|η − ξ| < ε. |
Поскольку ε > 0 — произвольное число, то это возможно только тогда, когда ξ = η (если бы ξ = η, то, например, при ε = |η − ξ| неравенство (4.26) было бы противоречиво). Это означает, что существует е д и н с т в е н н о е число ξ, принадлежащее всем отрезкам [an, bn]:
an ξ bn, n = 1, 2, ...
Из этих неравенств видно, что число ξ ограничивает сверху числа an и снизу числа bn, поэтому если α = sup {an}, β = inf {bn}, то в силу
определения верхней и нижней граней будут выполняться неравен-
ства
an α ξ β bn, n = 1, 2, ...
Таким образом, числа α, β и ξ принадлежат всем отрезкам [an, bn], а следовательно, по доказанному выше они равны, т. е. выполняется условие (4.25).
З а м е ч а н и е 1. Для интервалов и полуинтервалов множества действительных чисел аналог принципа вложенных отрезков не имеет места. Например,
n N 0, n1 |
= n N 0, n1 |
= . |
||||
|
|
|
|
|
|
|
З а м е ч а н и е 2. Для множества одних только рациональных чисел принцип вложенных отрезков несправедлив. При этом под

70 Гл. 1. Дифференциальное исчисление функций одной переменной
отрезком в множестве рациональных чисел понимается пересечение обычного отрезка, концы которого являются рациональными числами, с множеством рациональных чисел:
[a, b] ∩ Q = {x Q: a x b}, a Q, b Q.
Например, пусть числа a и b представляют собой десятичные при-
√ n n
ближения числа 2 с недостатком и с избытком и имеют по n десятичных знаков после запятой, n = 1, 2, ..., тогда
|
|
[an, bn] ∩ Q = , |
||||||
|
|
n N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так как |
[an, bn] = {√2 } и √2 — иррациональное число: √2 Q. |
|||||||
n N
4.6. Счетность рациональных чисел. Несчетность действительных чисел. Сравнение множеств осуществляется с помо-
щью понятия взаимно однозначного соответствия.
О п р е д е л е н и е 5. Два множества, между элементами которых
можно установить взаимно однозначное соответствие (биекцию), называются равномощными.
З а м е ч а н и е. Нетрудно убедиться, что если множество X равномощно множеству Y , а множество Y равномощно Z, то и множество X равномощно множеству Z.
Множество X называется конечным, если существует такое натуральное число n (называемое числом элементов множества X),
что между элементами множества X и элементами множества {1, 2, ...
..., n − 1, n} можно установить взаимно однозначное соответствие. Очевидно, два конечных множества равномощны тогда и толь-
ко тогда, когда они содержат одинаковое число элементов. Пустое
множество по определению считается конечным. Множества, не являющиеся конечными, называются бесконечными.
Приведем примеры равномощных бесконечных множеств.
П р и м е р ы. 1. Множество четных натуральных чисел равномощно множеству всех натуральных чисел. Действительно, соответствие n → 2n, n = 1, 2, ..., является биекцией множества натуральных чисел N и множества всех четных натуральных чисел.
2. Множество всех целых чисел равномощно множеству натуральных чисел. В самом деле, соответствие
2n → n, |
n = 1, 2, ..., |
2n + 1 → −n, |
n = 0, 1, 2, ..., |
является биекцией множества натуральных чисел N и множества целых чисел Z.

§ 4. Числовые множества |
71 |
3. Любые два конечных интервала (соответственно отрезка) числовой прямой равномощны. Если заданы два интервала (a, b) и (c, d), то отображение
x = |
(d − c)t + bc − ad |
, a < t < b, |
|
b − a |
|
является биекцией интервалов (a, b) и (c, d) (соответственно отрезков
[a, b] и [c, d]).
4. Множество всех действительных чисел R равномощно любому конечному интервалу числовой оси. В силу замечания после определения 5 и примера 3 достаточно показать, что множество действительных чисел равномощно хотя бы одному интервалу, поэтому
достаточно заметить, что функция y = |
t |
устанавливает взаимно |
2 |
||
1 |
− t |
|
однозначное соответствие между точками интервала (−1, 1) и точка- |
||
ми всей числовой оси. |
|
|
Примеры 1, 2 и 4 показывают, что в случае бесконечных множеств собственное подмножество бесконечного множества может оказаться равномощным всему множеству.
5. Пусть задано некоторое множество X. Всякое отображение мно-
жества натуральных чисел N в множество X, т. е. отображение вида f : N → X, называется последовательностью элементов множе-
ства X. Элемент f (n), n N, обозначается через xn и называется n-м
членом последовательности f : N → X, число n — его номером, и сам элемент f (n) X — значением этого члена.
Последовательность f : N → X обозначается также {xn} или xn, n = 1, 2, ...
Отметим, что член последовательности задается его значением и номером. Если n > m, то член последовательности xn называется членом, следующим за членом xm.
Множество членов последовательности равномощно с множеством натуральных чисел, так как каждому натуральному числу соответствует член последовательности и разным натуральным числам соответствуют разные члены последовательности, отличающиеся друг от друга по крайней мере номерами. Таким образом, множество членов последовательности всегда бесконечно, в то время как множество значений членов последовательности, т. е. множество значений функции f : N → X (иначе говоря, подмножество множества X, на которое посредством отображения f отображается множество N натуральных чисел), может оказаться конечным множеством, в частности состоять из одного элемента. В последнем случае, т. е. тогда, когда у после-
довательности все значения ее элементов совпадают, она называется
стационарной.
О п р е д е л е н и е 6. Множество, равномощное множеству натуральных чисел, называется счетным.

72 Гл. 1. Дифференциальное исчисление функций одной переменной
Ясно, что всякое счетное множество бесконечно, так как бесконечно множество натуральных чисел.
Из рассмотренных выше примеров 1, 2 и 5 следует, что множества всех четных чисел, всех целых чисел и всех членов любой последовательности являются счетными.
Пусть X — счетное множество, т. е. существует взаимно однозначное отображение (биекция) множества натуральных чисел N на множество X. Элемент множества X, соответствующий при этом отображении числу n, обозначим, как и в случае последовательности, xn и будем называть число n его номером. Поэтому можно сказать, что множество является счетным, если его элементы можно перенумеровать натуральными числами. Отличие определения счетного множества от последовательности состоит в том, что в случае последовательности рассматриваемое отображение множества натуральных чисел не обязано быть биекцией: не исключается случай, когда разным натуральным числам окажется поставленным в соответствие один и тот же элемент. Отсюда следует, что множество значений членов последовательности либо конечно, либо счетно, т. е., как говорят, не более чем счетно.
Ле м м а 1. Любое бесконечное множество содержит счетное подмножество.
Пусть X — бесконечное множество; тогда оно во всяком случае непусто, т. е. в нем существует по крайней мере один элемент, обозна-
чим его через x1. Поскольку множество X бесконечно, то множество X \ {x1} также непусто, т. е. содержит по крайней мере один элемент, обозначим его x2. Продолжая этот процесс, на n-м шаге получим
элемент xn. Поскольку X — бесконечное множество, то множество X \ {x1, x2, ..., xn} непусто, т. е. содержит по крайней мере один элемент, обозначим его xn+1 и т. д. Множество {x1, x2, ..., xn, ...} — искомое счетное подмножество множества X.
Ле м м а 2. Любое бесконечное подмножество счетного множества счетно.
Пусть X — счетное множество: X = {x1, x2, ..., xn, ...} и Y X. Обозначим через y1 элемент из Y , имеющий наименьший номер в X, через y2 — элемент множества Y , имеющий следующий ближайший номер, и т. д. Поскольку каждый элемент множества Y является некоторым элементом xn множества X и, следовательно, имеет номер n, то через конечное число шагов (не больше, чем n) он получает некоторый номер m и в множестве Y , т. е. будет обозначен ym, причем, поскольку множество Y бесконечно, этот процесс может быть продолжен
неограниченно. Таким образом, все элементы множества Y окажутся перенумерованными, что и означает счетность этого множества.
Те о р е м а 5. Множество всех рациональных чисел счетно.

§ 4. Числовые множества |
73 |
Расположим все рациональные числа в таблицу, содержащую бесконечное число строк и столбцов, следующим образом (см. таблицу):
0 |
1 |
−1 |
2 |
−2 ... |
|||||||||||
1 |
|
1 |
|
3 |
|
3 |
|
5 |
... |
||||||
|
|
|
− |
|
|
|
|
|
− |
|
|
|
|
||
2 |
|
2 |
2 |
|
2 |
2 |
|||||||||
. . . . . . . . . . . . . . . . . . . |
|||||||||||||||
|
1 |
|
− |
1 |
... ... ... ... |
||||||||||
|
n |
n |
|||||||||||||
. . . . . . . . . . . . . . . . . . . |
|||||||||||||||
Здесь в n-ю строчку помещены рациональные числа, записываемые несократимыми рациональными дробями со знаменателем n и упорядоченные по возрастанию их абсолютных величин, причем непосредственно за каждым положительным числом следует ему противоположное. Очевидно, что каждое рациональное число находится на каком-то месте в этой таблице.
Занумеруем теперь элементы получившейся таблицы согласно следующей схеме, в которой в кружочках стоят номера соот-
ветствующих элементов, а стрелки указывают направление нумерации.
В результате все рациональные числа оказываются занумерованными, т. е. множество Q рациональных чисел счетно.
Возникает естественный вопрос, существуют ли н е с ч е т н ы е множества, т. е.
бесконечные множества, не являющиеся счетными, а если существуют, то интересно построить пример несчетного множества.
Л е м м а 3. Любой отрезок множества действительных чисел состоит из несчетного множества точек.
Допустим противное: пусть точки некоторого отрезка [a, b], a R, b R, a < b, можно занумеровать: [a, b] = {x1, x2, ..., xn, ...}. Выберем какой-либо отрезок [a1, b1], лежащий на
[a, b] и не содержащий точки x1 (рис. 48): x1 [a1, b1] [a, b].
Далее выберем отрезок [a2, b2], лежащий
на [a1, b1] и не содержащий точки x2, и т. д. Таким образом, если выбран отрезок [an, bn], то выберем отрезок [an+1, bn+1], лежащий на [an, bn] и не содержащий точки xn+1. Продолжая этот процесс, получим систему вложенных отрезков [an, bn], n = 1, 2, ..., такую, что
|
xn [an, bn], |
n = 1, 2, ... |
(4.28) |
n |
Следовательно, ни одна точка xn не принадлежит пересечению |
||
|
вложенных |
отрезков (см. п. 4.5, |
|
∞ [an, bn], но согласно принципу |
|||
=1 |
|
|
|

74 Гл. 1. Дифференциальное исчисление функций одной переменной
теорема 3) существует точка, обозначим ее ξ, принадлежащая всем
отрезкам [an, bn]:
ξ [an, bn], n = 1, 2, ...,
а поэтому и отрезку [a, b], ибо [an, bn] [a, b] при всех n = 1, 2, ... А так как все точки отрезка [a, b] по предположению перенумерованы, то точка ξ также должна иметь какой-то номер, т. е. существует такое натуральное число n0, что ξ = xn0 , и тогда согласно (4.29) получим
xn0 [an, bn], n = 1, 2, ... |
(4.30) |
В частности, xn0 [an0 , bn0 ], а это противоречит условию (4.28).
Те о р е м а 6 (Кантор 1)). Множество всех действительных чисел несчетно.
Если бы множество всех действительных чисел было счетным, то было бы счетным, согласно лемме 2, и любое его подмножество,
вчастности, любой отрезок, что противоречит лемме 3.
§5. Предел числовой последовательности
5.1.Определение предела числовой последовательности.
Одним из важнейших понятий математического анализа является
понятие предела. Начнем его изучение с предела последовательности действительных чисел. Напомним (см. п. 1.4.6 , пример 5), что последовательностью {xn} элементов некоторого множества X называется отображение множества натуральных чисел в это множество X. Образ при этом отображении натурального числа n (член последовательно-
сти с номером n) в множестве X обозначается через xn. В частности, последовательностью действительных чисел является «занумерованное» натуральными числами некоторое множество x1, x2, ..., xn, ...
действительных чисел, причем члены последовательности с разными номерами могут иметь одно и то же значение. Примерами последо-
1, 13 , ..., n1 , ... и 1, 1, 1, ..., 1, ... В дальнейшем
вэтом параграфе буквой n всегда обозначаются натуральные числа.
Под бесконечно удаленной точкой числовой прямой будем понимать одну из бесконечностей +∞, −∞ или ∞ (см. п. 1.2.2).
О п р е д е л е н и е 1. Конечная или бесконечно удаленная точка числовой прямой называется пределом некоторой числовой последовательности действительных чисел, если какова бы ни была окрестность точки a, она содержит все члены рассматриваемой последовательности, начиная с некоторого номера.
Этот номер зависит, вообще говоря, от выбора окрестности точки a. Сформулированное условие равносильно тому, что вне любой
1) Г. Кантор (1845–1918) — немецкий математик.
§ 5. Предел числовой последовательности |
75 |
окрестности точки a находится лишь конечное число членов рассматриваемой последовательности. Вспомнив, что окрестности конечных и бесконечно удаленных точек числовой прямой определяются заданием некоторого числа ε > 0 (п. 1.2.2), определение предела последовательности действительных чисел можно перефразировать следующим образом.
Точка a (конечная или бесконечно удаленнная) числовой прямой называется пределом последовательности {xn} действительных чисел, если для любого ε > 0 существует такой номер nε, что для всех номеров n > nε члены xn содержатся в окрестности U (a; ε):
xn U (a; ε), n > nε. |
(5.1) |
Если выполняется это условие, то пишут lim xn = a или xn → a
n→∞
при n → ∞ (а иногда пишут xn → a, n = 1, 2, ...) и говорят, что члены последовательности {xn} стремятся к a.
С помощью логических символов существования и всеобщности определение предела записывается следующим образом:
a = nlim |
def |
xn U (a; ε). |
(5.2) |
xn ε > 0 nε : n > nε |
|||
→∞ |
|
|
|
Если предел последовательности действительных чисел является
конечной точкой числовой прямой, т. е. числом, то говорят, что последовательность имеет конечный предел.
О п р е д е л е н и е 2. Если числовая последовательность имеет конечный предел, то она называется сходящейся.
Для случая конечного предела определение 1 предела можно перефразировать следующим образом.
Число a является пределом последовательности {xn} действительных чисел, если для любого ε > 0 существует такой номер nε, что для всех номеров n > nε выполняется неравенство
|xn − a| < ε. |
(5.3) |
В логических символах эта формулировка выглядит следующим образом:
a = nlim |
def |
(5.4) |
xn ε > 0 nε n > nε : |xn − a| < ε. |
||
→∞ |
|
|
Очевидно, что неравенство (5.3) равносильно неравенству |
|
|
|
a − ε < xn < a + ε. |
(5.5) |
Аналогичным образом формулируются и определения предела числовой последовательности в случае, когда этот предел является той или иной бесконечно удаленной точкой (или, как говорят, равен бесконечности).

76 Гл. 1. Дифференциальное исчисление функций одной переменной
Например, согласно определению (5.2) ∞ является пределом последовательности {xn}, если для любого ε > 0 существует такой номер nε, что для всех номеров n > nε выполняется включение
xn U (∞; ε), |
(5.6) |
или, что то же самое, неравенство |
|
|xn| > 1/ε. |
(5.7) |
В логических символах это утверждение записывается следующим образом:
nlim |
def |
n > nε : |xn| > 1/ε. |
(5.8) |
xn = ∞ ε > 0 nε |
|||
→∞ |
|
|
|
Аналогичным образом определение предела последовательности перефразируется для случая, когда этот предел равен бесконечности со знаком. Для краткости ограничимся записью этих определений только с помощью логических символов:
nlim |
def |
xn = +∞ ε > 0 |
|
→∞ |
|
nlim |
def |
xn = −∞ ε > 0 |
|
→∞ |
|
nε n > nε : |
xn > 1/ε, |
nε n > nε : |
xn < −1/ε. |
Заметим, что если ε — произвольное положительное число, то и 1/ε — также произвольное положительное число.
Очевидно, что если nlim xn =+∞ или |
nlim xn =−∞, то и nlim xn = |
||
= ∞. |
→∞ |
→∞ |
→∞ |
|
|
|
|
О п р е д е л е н и е 3. Последовательность, пределом которой является бесконечность (со знаком или без знака), называется бесконечно большой.
П р и м е р ы. 1. Последовательность xn = 1/n, n = 1, 2, ..., сходится и имеет своим пределом нуль. Действительно, каково бы ни было ε > 0, согласно принципу Архимеда существует натуральное nε, большее, чем 1/ε, т. е. nε > 1/ε и, следовательно, 1/nε < ε, а тогда для всех натуральных n > nε имеет место неравенство
|
0 < |
1 |
< |
1 |
|
< ε. |
|||||
|
n |
nε |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
Таким образом, при n > nε выполняется условие |
|||||||||||
|
|
1 |
− 0 = |
1 |
|
< ε, |
|||||
|
n |
n |
|||||||||
|
1 |
|
|
|
|
|
|
|
|
||
а это и означает, что lim |
|
|
= 0. |
|
|
|
|
||||
|
|
|
|
|
|||||||
n→∞ n |
|
|
n |
, |
n = 1, 2, ..., не имеет предела, |
||||||
2. Последовательность xn = (−1) |
|
||||||||||
так как какое бы число a ни взять, вне любой его ε-окрестности при ε < 1 будет находиться бесконечно много членов указанной последовательности.
