IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

2. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

3. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

Лабораторная работа № 13

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КРАТНЫХ

ИНТЕГРАЛОВ МЕТОДОМ ЯЧЕЕК

ЦЕЛЬ РАБОТЫ

Приобретение навыков приближенного вычисления кратных интегралов.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Построим кубатурную формулу, предназначенную для приближенного вычисления двойных интегралов

Рассмотрим метод ячеек.

Пусть область интегрирования представляет собой прямоугольникРазобьем областьна прямоугольные ячейки (рис. 1).

Р

ююю

ю

оо

ис. 1.

Используя формулу средних для вычисления интеграла по каждой ячейке и обозначая через соответственно площадьячейки и координаты ее центра, получим

Для любой непрерывной функции интегральная сумма сходится к значению интеграла, когда периметры всех ячеек стремятся к нулю.

Если стороны прямоугольника разбиты соответственно на иравных частей, то погрешность обобщенной формулы (2)

В случае, когда область не является прямоугольником, на нее следует наложить прямоугольную сетку (рис. 2).

Рис. 2

Ячейки, которые полностью лежат в области , называются внутренними. Ячейка называется граничной, если часть ее принадлежит, а часть находится вне. Площадь внутренней ячейки равна произведению ее сторон. Площадью граничной ячейки будем считать площадь той ее части, которая принадлежит. Эту площадь вычислим приближенно, заменяя истинную границу на хорду. Указанные выше площади подставим в формулуи найдем приближенное значение интеграла.

ЗАДАНИЕ

Методом ячеек вычислить интеграл по области, изображенной на рис. 3.

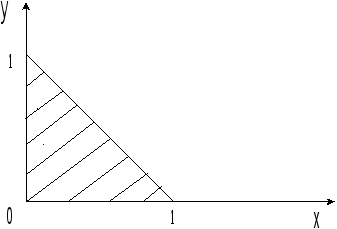
Рис. 3

Варианты заданий

Номер варианта
1
2
3
4
5
6
7
8
9
10
1	2
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

Здесь - последняя цифра номера группы.