
- •Сборник методических указаний к лабораторным работам
- •Численные Методы
- •Методические указания к лабораторным работам составлены профессором кафедры пМиИ Толоконниковым л.А. И обсуждены на заседании кафедры пМиИ механико-математического факультета,
- •Содержание
- •Лабораторная работа № 1 решение систем линейных алгебраических уравнений методом гаусса с выбором главного элемента
- •IV. Оформление отчета
- •IV. Оформление отчета в отчете должны быть представлены:
- •Лабораторная работа № 3 решение систем линейных уравнений методом зейделя
- •IV. Оформление отчета в отчете должны быть представлены:
- •Лабораторная работа № 4 решение систем с трехдиагональной матрицей методом прогонки
- •IV. Оформление отчета
- •IV. Оформление отчета
- •IV. Оформление отчета
- •IV. Оформление отчета в отчете должны быть представлены:
- •Лабораторная работа № 8 решение нелинейного уравнения методом ньютона
- •IV. Оформление отчета в отчете должны быть представлены:
- •Лабораторная работа № 9 применение интерполяционной формулы лагранжа
- •IV. Оформление отчета в отчете должны быть представлены:
- •Лабораторная работа № 10
- •IV. Оформление отчета
- •IV. Оформление отчета
- •IV. Оформление отчета
- •IV. Оформление отчета
- •IV. Оформление отчета в отчете должны быть представлены:
- •Лабораторная работа № 15 решение обыкновенных дифференциальных уравнений методом рунге – кутта
- •IV. Оформление отчета в отчете должны быть представлены:
- •Лабораторная работа № 16 применение разностного метода для решения обыкновенного дифференциального уравнения с краевыми условиями
- •IV. Оформление отчета в отчете должны быть представлены:
- •Лабораторная работа №17 решение уравнений эллиптического типа методом сеток
- •IV. Оформление отчета
- •IV. Оформление отчета в отчете должны быть представлены:
- •Лабораторная работа № 19 решение уравнений гиперболического типа методом сеток
- •IV. Оформление отчета в отчете должны быть представлены:
- •Лабораторная работа № 20 решение интегральных уравнений с помощью квадратурных формул
- •В отчете должны быть представлены:
- •Лабораторная работа № 21
- •В отчете должны быть представлены:
- •Лабораторная работа № 22 решение плохо обусловленных систем линейных алгебраических уравнений
- •В отчете должны быть представлены:
- •Лабораторная работа № 23 решение линейных интегральных уравнений первого рода
- •В отчете должны быть представлены:
Лабораторная работа № 9 применение интерполяционной формулы лагранжа
ЦЕЛЬ РАБОТЫ
Приобретение навыков использования интерполяционных многочленов.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Пусть
функция
![]() задана таблично, т.е. известны ее значения
в
задана таблично, т.е. известны ее значения
в![]() точках
точках![]()
![]() (
(![]() ).
(1)
).
(1)
Построим
многочлен
![]() степени
степени![]() такой, чтобы выполнялись интерполяционные
условия
такой, чтобы выполнялись интерполяционные
условия
![]() (
(![]() ).
(2)
).
(2)
Сначала
построим полином степени
![]()
![]() ,
такой, что
,
такой, что
![]() ,
(3)
,
(3)
где
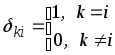 - символ Кронекера.
- символ Кронекера.
Так
как
![]() обращается в нуль в
обращается в нуль в![]() точках
точках![]() ,
то он имеет вид
,
то он имеет вид
![]() ,
(4)
,
(4)
где
![]() - постоянный коэффициент.
- постоянный коэффициент.
Полагая
в формуле (4)
![]() и учитывая, что
и учитывая, что![]() ,
получим
,
получим
![]() .
.
Подставив этот коэффициент в (4), находим
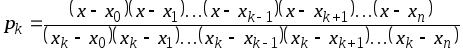 .
(5)
.
(5)
Теперь
построим многочлен
![]() ,
который имеет вид
,
который имеет вид
![]() .
(6)
.
(6)
Степень
![]() ,
как видно из (5) и (6), не выше
,
как видно из (5) и (6), не выше![]() .
Кроме того, на основании (2)
.
Кроме того, на основании (2)
![]() ,
,
что согласуется с (2)
Интерполяционный
многочлен
![]() называется многочленом Лагранжа и имеет
вид
называется многочленом Лагранжа и имеет
вид
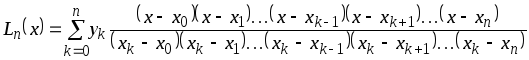 .
.
Теперь
считаем
![]() .
.
Для абсолютной погрешности интерполяционного многочлена Лагранжа справедлива оценка
![]() ,
,
где
![]() ;
;
![]() .
.
ЗАДАНИЕ
Дана
таблица значений функции
![]()
-
x
3,5
4,1
4,3
5
y
N+k
N+2k
N-k
N
Здесь
![]() -
номер фамилии студента в журнале группы;
-
номер фамилии студента в журнале группы;![]() -
последняя цифра номера группы.
-
последняя цифра номера группы.
Построить
интерполяционный многочлен Лагранжа.
Вычислить с его помощью значения
![]() ;
;
![]() ;
;
![]() .
.
IV. Оформление отчета в отчете должны быть представлены:
1. Название работы.
2. Постановка задачи.
3. Описание алгоритма (метода) решения.
4. Текст программы с описанием.
5. Результаты работы программы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.
2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.
3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.
Лабораторная работа № 10
ИНТЕРПОЛИРОВАНИЕ КУБИЧЕСКИМИ СПЛАЙНАМИ
ЦЕЛЬ РАБОТЫ
Приобретение навыков использования интерполяционных сплайнов.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Пусть
на
![]() в узлах сетки
в узлах сетки![]() заданы значения некоторой функции
заданы значения некоторой функции![]()
![]()
Для
интерполирования функций воспользуемся
кубическими сплайнами дефекта 1, которые
обозначим
![]() На каждом из промежутков
На каждом из промежутков![]() сплайн
сплайн![]() записывается в виде
записывается в виде
![]()
Причем
![]()
Рассмотрим
два алгоритма построения интерполяционных
кубических сплайнов, удовлетворяющих
условиям
![]()
Введем
обозначение
![]()
Решая систему уравнений
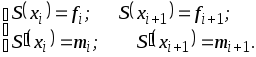
Найдем
коэффициенты
![]()
![]()
В
результате выражение
![]() примет вид
примет вид
![]() где
где
![]()
Кубический
сплайн
![]() ,
записанный в терминах
,
записанный в терминах![]() ,
на каждом из промежутков
,
на каждом из промежутков![]() непрерывен вместе со своей первой
производной всюду на
непрерывен вместе со своей первой
производной всюду на![]() Выберем величины
Выберем величины![]() так,
чтобы была непрерывна и вторая производная
сплайна. Условие
так,
чтобы была непрерывна и вторая производная
сплайна. Условие
![]()
дает
![]() уравнений для нахождения
уравнений для нахождения![]()
![]()
где

К
уравнениям
![]() следует присоединить еще два уравнения,
являющихся краевыми условиями. Из
полученной системы уравнений находятся
значения величин
следует присоединить еще два уравнения,
являющихся краевыми условиями. Из
полученной системы уравнений находятся
значения величин![]() которые подставляются в выражение для
интерполяционного сплайна
которые подставляются в выражение для
интерполяционного сплайна![]()
Если
ввести обозначение
![]() и коэффициенты
и коэффициенты![]() найти как решение системы уравнений
найти как решение системы уравнений
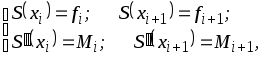
то
на каждом
![]() интерполяционный кубический сплайн в
терминах
интерполяционный кубический сплайн в
терминах![]() будет представляться выражением
будет представляться выражением

При
этом сплайн
![]() и его вторая производная будут непрерывны
на
и его вторая производная будут непрерывны
на![]() Выберем величины
Выберем величины![]() так, чтобы была непрерывна и первая
производная сплайна. Условие
так, чтобы была непрерывна и первая
производная сплайна. Условие![]()
дает
![]() уравнений
уравнений
![]()
![]()
где
![]()
К
уравнениям
![]() следует присоединить два краевых
условия. Из полученной системы уравнений
находятся значения
следует присоединить два краевых
условия. Из полученной системы уравнений
находятся значения![]() которые подставляются в выражение
которые подставляются в выражение![]()
На практике наиболее употребительными являются краевые условия следующих типов:
ЗАДАНИЕ
С
помощью интерполяционных кубических
сплайнов, записанных в терминах
![]() и
и![]() ,
вычислить значения функции
,
вычислить значения функции![]() в точках
в точках![]() Таблица значений функции
Таблица значений функции![]() приведена в лабораторной работе № 9.
приведена в лабораторной работе № 9.
Использовать следующие краевые условия
![]()
Указания:
При использовании сплайнов, записанных в терминах
 к уравнениям
к уравнениям присоединить следующие уравнения:
присоединить следующие уравнения:
![]()
где
![]()
При использовании сплайнов, записанных в терминах
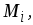 к уравнениям
к уравнениям присоединить следующие уравнения:
присоединить следующие уравнения:
![]()
Cистемы
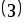 и
и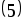 являются системами с трехдиагональной
матрицей. Осуществить их решение методом
прогонки.
являются системами с трехдиагональной
матрицей. Осуществить их решение методом
прогонки.
