IV. Оформление отчета в отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. 350 с.

Лабораторная работа № 8 решение нелинейного уравнения методом ньютона

2. ЦЕЛЬ РАБОТЫ

Приобретение навыков отыскания приближенных значений действительных корней уравнения методом Ньютона.

2. ТЕОРЕТИЧЕСКАЯ СПРАВКА

Требуется найти корни уравнения

, (1)

где - дифференцируемая функция.

Если есть некоторое приближение к корню, аимеет непрерывную производную, то уравнение (1) можно преобразовать следующим образом:

,

где - точка, лежащая междуи.

Приближенно заменяя на значение в известной точке, получим такой итерационный процесс:

Геометрически этот процесс означает замену на каждой итерации графика касательной к нему.

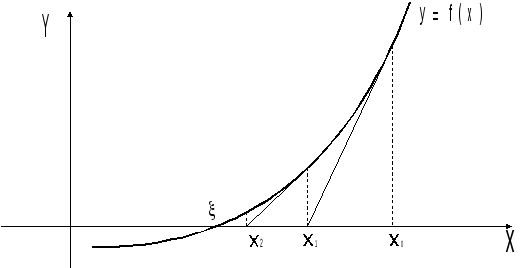
Метод Ньютона можно рассматривать как частный случай метода итераций, если положить

Тогда

При произвольном начальном приближении итерации сходятся, если всюду на рассматриваемом интервале (чтобы, причем). В противном случае сходимость будет не при любом начальном приближении, а только в некоторой окрестности корня.

Отметим еще достаточное условие сходимости итераций: если иотличны от нуля и сохраняют определенные знаки на, то исходя из начального приближения, удовлетворяющего неравенству, получим методом Ньютона значение корня с любой степенью точности. Т.о., в качестве исходной точкиследует выбирать тот конец, для которогоиимеют одинаковые знаки. Если взять такое, что, то мы можем не прийти к корню, если тольконе очень хорошее.

Оценим скорость сходимости метода Ньютона. Справедлива оценка

,

где - наибольшее значениена,;- наименьшее значениена,. Отсюда видно, что погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Самый неблагоприятный случай для метода Ньютона, когдастановится малой вблизи корня. Чтобы не было потери точности, отношениенадо вычислять достаточно аккуратно. К остальным погрешностям расчета метод Ньютона хорошо устойчив.

3. ЗАДАНИЕ

Найти методом Ньютона один из действительных корней уравнения с точностью. Варианты заданий приведены в лабораторной работе № 6.

IV. Оформление отчета в отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. 350 с.