
Матика 2 курс / Специальные главы математики 140410(ЭАб)
.pdf
51
x tg(z y) 2x
11)y 
 9 12x 3e yz 3y
9 12x 3e yz 3y
|
|
x e x e3z |
|
|
|
|
|
12) |
y 4z 3sin(x y) |
||
|
z ln(1 z 3x) |
||
|
|||
|
|
||
2.Исследовать, при каких значениях параметров нулевое решение системы
является устойчивым
ВАРИАНТЫ
x y sin x
1)y ax by y2
|
|
|
2e |
x |
|
4 ay |
2) |
|
|||||
x |
|
|
||||
|
y ln(1 9x ay) |
|||||
x ax 2 y x2
2)y x y xy
x ln( e ax) e y
4)y bx tgy
РГР 10. Элементы вариационного исчисления. Экстремали.
Литература
Гюнтер Н.М. Курс вариационного исчисления [электронный ресурс] / Н. М.
Гюнтер. – СПб.: Лань, 2009. – 320 с.
1. Задачи с закрепленными границами
Простейшей вариационной задачей называют задачу нахождения экстремума функционала
b
J ( y(x)) F(x, y(x), y (x)) dx
a
на множестве непрерывно дифференцируемых функций y (x) , заданных на отрезке a, b и удовлетворяющих условиям y (a) A, y (b) B .
Функция, которая доставляет экстремум функционалу, называется экстремалью. Если функция y (x) дважды непрерывно дифференцируема на

52
a, b и является экстремалью, то она необходимо удовлетворяет уравнению Эйлера:
F d F 0 .
y dx y
В некоторых случаях решение уравнения Эйлера упрощается по сравнению с общим случаем
1.Функция F(x, y) в выражении для функционала явно не зависит от y : F(x, y) 0 ( это уравнение не является дифференциальным) ;
2. |
Функция F( y ) зависит только от |
y : |
2 F |
y 0 . Общим решением |
||||
y 2 |
||||||||
|
|
|
|
|
|
|||
|
этого уравнения являются прямые линии y C1x C2 |
|||||||
|
|
|
|
|
|
|
||
3. |
Функция F(x, y ) не зависит от y : |
|
|
F ( x, y ) |
C1 |
|||
|
|
|
y |
|||||
|
|
|
|
|
|
|||
4. |
Функция явно F( y, y ) не зависит от x : |
|
|
|
||||
|
|
|
|
|
|
|
||
|
F ( y, y ) |
|
||||||
|
F ( y, y ) y |
|
|
|
|
|
C1 . |
|
|
|
|
y |
|||||
|
|
|
|
|
||||
ВАРИАНТЫ (в скобках ответы)
Найти экстремали функционала, удовлетворяющие заданным граничным условиям.
|
|
|
|
2 |
y |
|
|
y(0) y( ) 0 |
1) |
|
|
|
2 |
)dx, |
|||
I ( y) (4 y cos x ( y ) |
|
|||||||
|
0 |
|
|
|
|
|
|
|
( y sin x(C x) ) |
|
|
|
|
|
|
|
|
|
e |
|
2 |
|
|
|
|
|
2) |
I ( y) (2 y x |
2 |
dx, |
y(1) e, y(e) 0 |
||||
|
( y ) |
|||||||
1

|
|
|
|
|
|
|
|
|
|
|
|
|
|
53 |
|
|
( y |
e |
ln x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
yy |
|
12xy)dx, |
y(0) y(1) 0 |
|||||||||
|
|
|
|
|
||||||||||||
3) I ( y) (( y ) |
|
|
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( y x3 x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
ln 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
|
|
|
2 |
3y |
2 |
|
2 x |
|
|
y(0) 0, y(ln 2) |
15/ 8 |
|
|||
I ( y) (( y ) |
|
|
)e |
|
|
dx, |
|
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( y e x e 3x ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. |
Материальная |
|
точка |
перемещается |
вдоль |
плоской кривой y y(x), |
||||||||||
|
соединяющей |
точки |
|
M 0 (0,0) и |
M1 (1,1) со |
скоростью v x . Найдите |
||||||||||
кривую, двигаясь по которой материальная точка попадет из одной точки в
другую за наименьшее время. (Ответ: y |
1 x 2 |
1) |
2.Задача о брахистохроне. Найдите плоскую кривую, соединяющую точки M 0 (0,0) и M1 (x1 , y1 ) , при скатывании вдоль которой под действием силы
тяжести материальная точка
наименьшее время. Ответ:
перемещается из M 0 (0,0) в M1 (x1 , y1 ) за
|
C |
|
|
x |
|
(t sin t) |
|
2 |
|||
|
|
||
C |
|
||
y |
(1 cost) |
||
|
|||
|
2 |
|
2.Задачи с подвижными границами
Простейшая задача вариационного исчисления с подвижными границами состоит в определении функции  , принадлежащей отрезку
, принадлежащей отрезку  и точек
и точек
для которых функционал
достигает экстремума при условиях  ,
,  Эту задачу можно сформулировать также следующим образом. Пусть на плоскости заданы гладкие кривые
Эту задачу можно сформулировать также следующим образом. Пусть на плоскости заданы гладкие кривые

54
Требуется найти такую гладкую кривую  которая соединяет какуюлибо точку кривой
которая соединяет какуюлибо точку кривой  с какой-либо точкой кривой
с какой-либо точкой кривой  и доставляет экстремум функционалу.
и доставляет экстремум функционалу.
Рис 1.
Рассмотренная ранее задача, когда граничные условия были зафиксированы :
 является частным случаем задачи с подвижными границами.
является частным случаем задачи с подвижными границами.
Поэтому искомая кривая  должна быть экстремалью, то есть должна удовлетворять уравнению Эйлера :
должна быть экстремалью, то есть должна удовлетворять уравнению Эйлера :
Однако, в задаче с подвижными границами одно из условий
 или оба эти условия отсутствуют. Поэтому для определения произвольных постоянных, возникающих при решении задачи, необходимы некоторые условия. Условия для нахождения произвольных постоянных в
или оба эти условия отсутствуют. Поэтому для определения произвольных постоянных, возникающих при решении задачи, необходимы некоторые условия. Условия для нахождения произвольных постоянных в
задаче с подвижными границами называют условиями трансверсальности.
Найдем эти условия, взяв за основу необходимое условие существования экстремума функционала :
При этом будем считать, что кривая |
является экстремалью. |
|
||
Рассмотрим случай, когда одна из граничных точек закреплена : |
а |
|||
другая может перемещаться вдоль кривой |
Пусть |
– кривая, близкая к |
||
искомой |
. |
|
|
|
Запишем приращение функционала при переходе от |
к точке |
|
||
 :
:

55
9x)
Рис.2.
Второй интеграл в этой сумме оценим по теореме о среднем

56
Приближенно можно считать
(2)
В первом интеграле этой суммы заменим приращение  по переменным
по переменным  дифференциалом (или представим по формуле Тейлора для функции двух
дифференциалом (или представим по формуле Тейлора для функции двух
переменных с точностью до линейных слагаемых):
С учетом того, что точка  закреплена
закреплена  а искомая кривая удовлетворяет уравнению Эйлера :
а искомая кривая удовлетворяет уравнению Эйлера :
получаем для вариации фукнционала выражение

57
С учетом того, что
Таким образом, необходимые условия существования экстремума
функционала записываются в виде:
(4)
При условии перемещения правой граничной точки по кривой получаем для вариации функции
Поэтому условия (4) имеют вид:
(5)
Полученное условие и называют условием трансверсальности.
Если левая граничная точка также перемещается по кривой  , то добавляется аналогичное условие
, то добавляется аналогичное условие
(5a)
Частные случаи условий трансверсальности
1.Если одна из граничных точек, например, правая  перемещается по горизонтальной прямой
перемещается по горизонтальной прямой  то
то 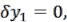 и условие трансверсальности записываем как
и условие трансверсальности записываем как

58
(6)
2. Если задана абсцисса одного из концов, а граничное условие отсутствует,
то это |
означает, что граничная |
точка |
может |
перемещаться по |
вертикальной прямой, например, |
. |
Тогда |
вместо условия |
|
трансверсальности записывают условие |
|
|
|
|
Примеры решения задач
Задача 1.
Найти кривую минимальной длины, соединяющую параболу  и прямую
и прямую  Решение.
Решение.
Функционалом в данном случае является длина дуги
Пусть левая граничная точка перемещается по параболе  а правая по прямой
а правая по прямой  Функция
Функция 
Шаг 1. Составляем и решаем уравнение Эйлера: 
Имеет место частный случай, когда функция F зависит только от

59
Тогда |
, а |
; |
Общее решение такого уравнения имеет вид |
||
Заметим, что |
|
|
|
. |
(8) |
Шаг 2. С учетом того, что искомая кривая и линии, по которым перемещаются граничные точки, должны пересекаться, получаем условие:
В данной задаче:  ,
, 
Шаг 3. Записываем условия трансверсальности
С учетом условия (8):
Шаг 4. Для определения 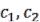 решаем систему уравнений
решаем систему уравнений

60
Вычитая из первого уравнения системы второе, получаем
 .
.
Подставляя  в третье уравнение системы, получаем соотношение между
в третье уравнение системы, получаем соотношение между 
Подстановка этого соотношения в первое уравнение системы дает: 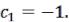
Тогда  Из четвертого уравнения системы получаем
Из четвертого уравнения системы получаем
Уравнение искомой кривой: 
Расстояние между параболой и прямой:
Задача2.
Поскольку отсутствует граничное условие для левой граничной точки, то принято считать, что левый конец движется по вертикальной линии. В этом
случае граничное условие имеет вид: 
Решая уравнение Эйлера, находим уравнение экстремали:
