Корреляционная матрица парных коэффициентов корреляции для переменных x4-x7 , x10-x13

Построим корреляционную матрицу частных коэффициен­тов корреляции :

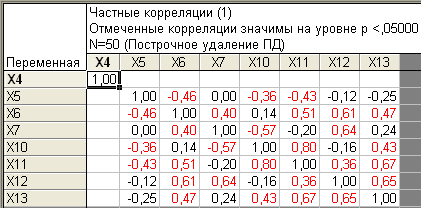
Корреляционная матрица частных коэффициентов корреляции

Если сравнить рассчитанные парные и частные коэффициенты корреляции можно заметить, что влияние других переменных, что характерно для частных коэффициентов корреляции, в некоторых случаях изменяет тесноту зависимостей, и отдельные коэффициенты корреляции, значимые при расчете парных взаимосвязей, становятся незначимыми при расчете частных взаимосвязей. Данная особенность проявилась, между переменными x₇ (денежные средства организации) и x₁₀ (нераспределенная прибыль прошлых лет). Это можно объяснить тем, что между данными показателями относительно слабая взаимосвязь. Таким образом, проведение корреляционного анализа позволяет выявить показатели, наиболее тесно связанные между собой, оценить направление анализируемых взаимосвязей, просмотреть исследуемые зависимости графически, а также определить наблюдения, удаление которых из исследуемой совокупности приводит к существенным изменениям тесноты оцениваемых связей.

2.3. Вывод

В рассматриваемом примере наиболее тесной является зависимость между переменной x₁₁ и переменной x₆, т.к. коэффициент корреляции при данных переменных r_x11x6 = 0,77 наиболее близок к 1. Следовательно, можно предположить, что финансовый показатель - прочие доходы и среднесписочная численность работников, тесно связаны между собой.

Таким образом, проведение корреляционного анализа позволиловы-явить показатели, наиболее тесно связанные между собой, оценить направление анализируемых взаимосвязей, просмотреть исследуемые зависимости графически, а также определить наблюдения, удаление которых из исследуемой совокупности приводит к существенным изменениям тесноты оцениваемых связей.

Кластерный анализ Вариант 32

3.1. Постановка задачи:

1. Провести классификацию регионов Приволжского Федерального округа с использованием иерархических агломеративных методов и метода k-средних по величине численности безработных. Выделить группы регионов применяя различные методы объединения кластеров. Построить дендограммы. Провести сравнительный анализ регионов по выделенным кластерам используя сравнения средних значений по кластерам и построением графика k-средних.

2. Классификацию провести за два временных периода: 1995-2005гг. и 2006-2009гг. Провести анализ формирования кластеров в различные временные периоды. Сравнить произошедшие изменения по численности безработных в регионах в зависимости от принадлежности их к определенным кластерам в разное время. Сравнить средние значения регионов, сформировавших различные кластеры со средним значением данного показателя по Приволжскому Федеральному округу.

ЧИСЛЕННОСТЬ БЕЗРАБОТНЫХ (тысяч человек)

Таблица 10 – исходные данные

	1995	2000	2001	2002	2003	2004	2005	2006	2007	2008	2009
Приволжский федеральный округ	1377	1543	1306	1199	1180	1217	1152	1028	969	1010	1385
Республика Башкортостан	144	228	205	161	161	138	143	130	133	106	191
Республика Марий Эл	41	44	34	51	44	35	38	37	34	34	42
Республика Мордовия	52	47	44	40	32	26	30	21	16	11	25
Республика Татарстан	120	159	116	100	126	137	127	107	108	96	169
Удмуртская Республика	94	78	59	65	54	64	64	71	66	66	74
Чувашская Республика	66	61	63	63	56	65	75	59	60	55	79
Пермский край	130	152	98	131	99	101	99	99	94	123	146
Кировская область	72	68	64	56	58	70	57	62	46	57	84
Нижегородская область	160	144	149	142	112	134	107	95	83	102	136
Оренбургская область	76	127	86	105	118	116	99	71	78	75	96
Пензенская область	102	86	100	51	62	48	47	46	36	55	54
Самарская область	126	174	104	94	74	92	92	76	76	74	107
Саратовская область	138	130	126	98	135	128	121	109	108	104	119
Ульяновская область	56	45	57	43	48	64	53	47	32	51	61