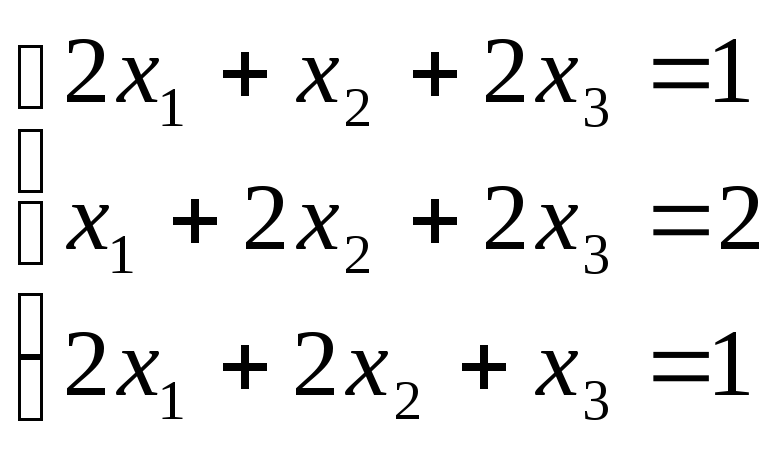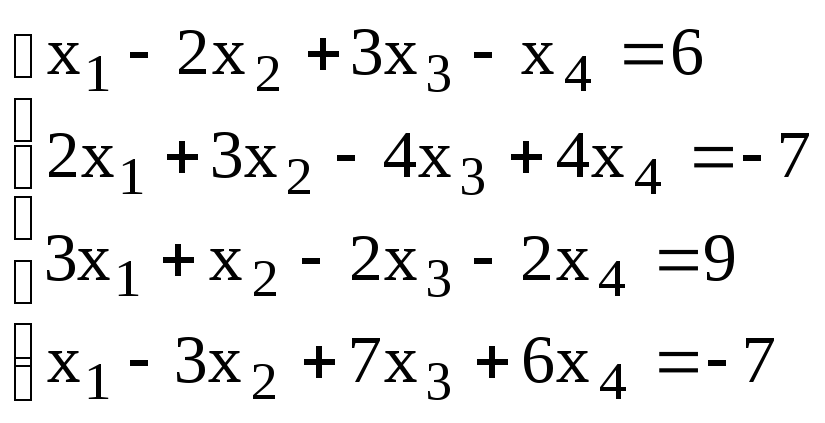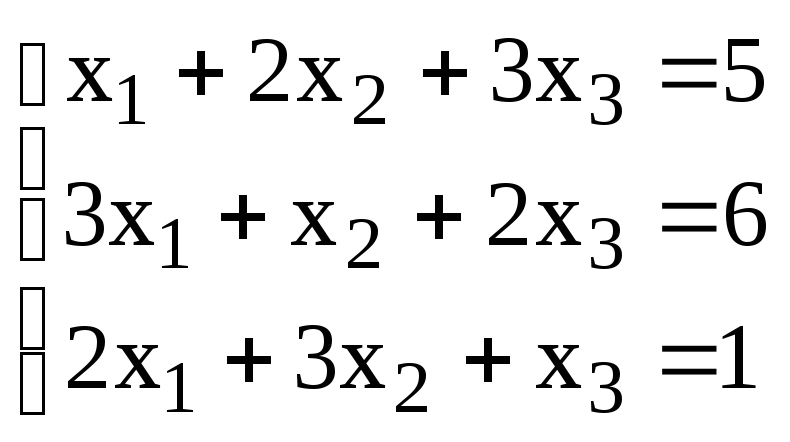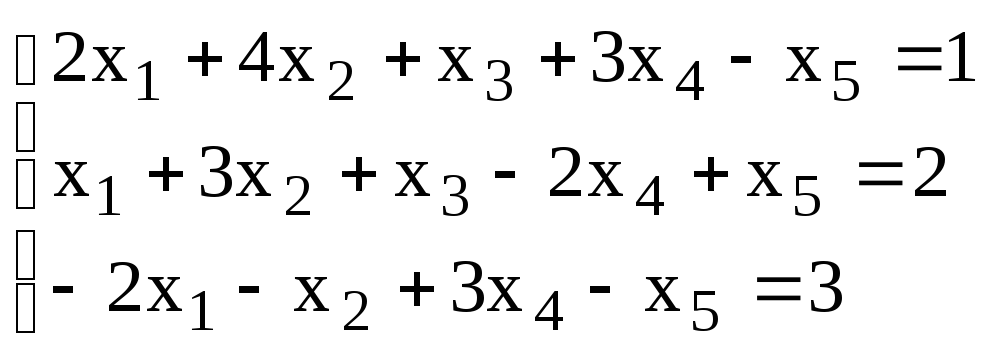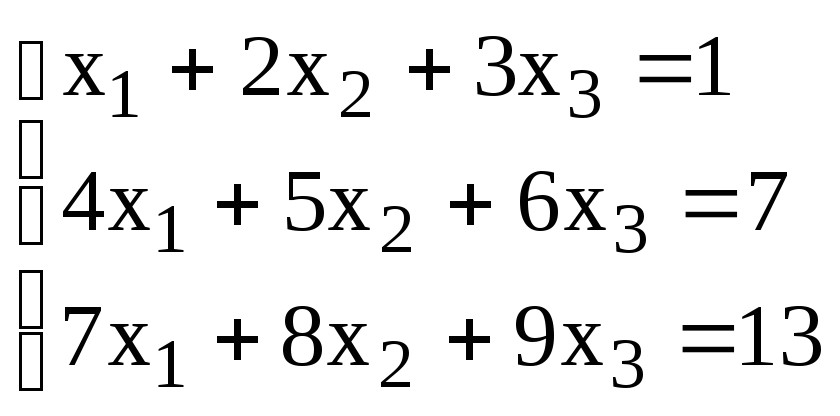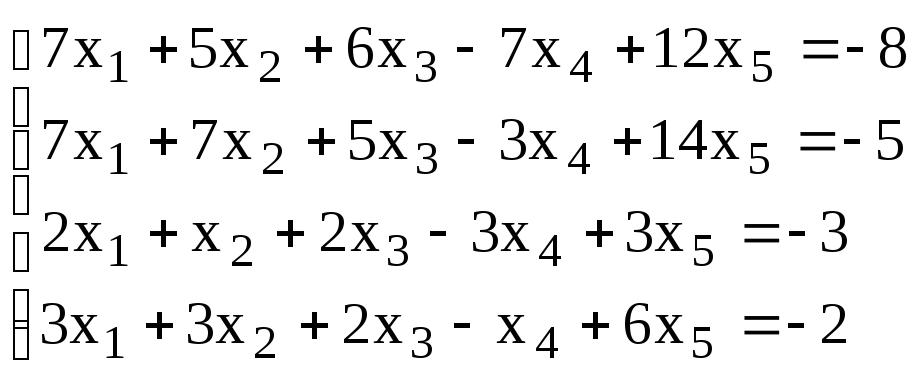Линейная алгебра. Векторная алгебра. Аналитическая геометрия

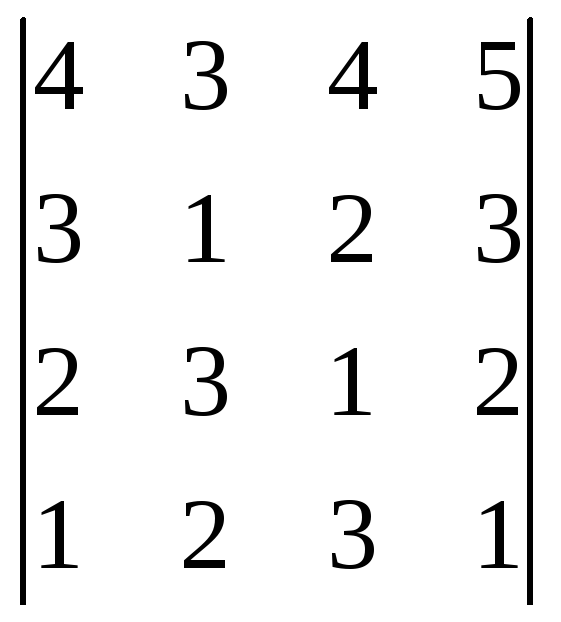
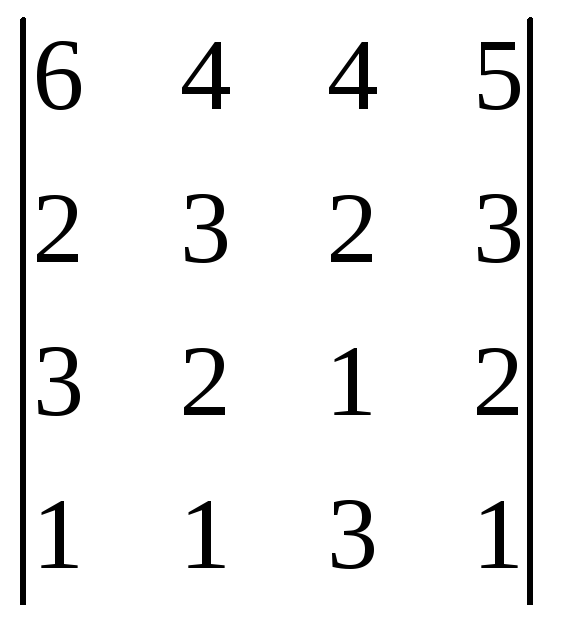
1. Упростить и вычислить определитель.

2. Решить матричным методом.

3. Решить систему методом Гаусса

4. Векторы ивзаимно перпендикулярны, векторобразует с ними углы, равные 60. Зная, что,,, вычислить

5. Найти проекцию вектора на вектор, если , , .

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороныBC; 2) уравнение линииBC; 3) уравнение высоты, проведенной из точкиA; 4) величину углаB; 5) систему неравенств, определяющую треугольникABC. Сделать чертеж.

A (6,2), B (30,-5), C (12,19)

7. Даны стороны треугольника и, точка Р(1,2) - точка пересечения третьей стороны с высотой. Найти уравнение третьей стороны.

8. Даны координаты вершин пирамида АВСД. Требуется найти: 1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскостиABC,. Сделать чертеж.

А (3,1,4); В (-1,6,1); С (-1,1,6); D(0,4,-1)

1. Упростить и вычислить определитель.

2. Решить матричным методом.

3. Решить систему методом Гаусса

4. Вычислить длину вектора , если,,,, угол между ними.

5. Вектор коллинеарен вектору и образует тупой угол с осьюOZ. Зная, что, найти его координаты.

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороныBC; 2) уравнение линииBC; 3) уравнение высоты, проведенной из точкиA; 4) величину углаB; 5) систему неравенств, определяющую треугольникABC. Сделать чертеж.

A (4,3), B (-12,-9), C (-5,15)

7. Найти точку В, симметричную точке А(-2,4) относительно прямой, проходящей через точки М(1,5) и Р(2,2).

8. Даны координаты вершин пирамида АВСД. Требуется найти: 1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскостиABC,. Сделать чертеж.

А (3,3,9); В (6,9,1); С (1,7,3); D(8,5,8)

1. Упростить и вычислить определитель.

2. Решить матричным методом.

3. Решить систему методом Гаусса

4. Векторы иобразует угол 270°. Зная, что,, вычислить.

5. Вектор образует острый угол с осью ОХ и коллинеарен век­тору ,. Найти вектор.

6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороныBC; 2) уравнение линииBC; 3) уравнение высоты, проведенной из точкиA; 4) величину углаB; 5) систему неравенств, определяющую треугольникABC. Сделать чертеж.

A (-1,7), B (11,2), C (17,10)

7. Дан треугольник с вершинами А(-8,3), B(8,5), С(8,-5). Найти точку пересечения его высот.

8. Даны координаты вершин пирамида АВСД. Требуется найти: 1) длину ребра , 2) угол между ребрамии, 3) проекцию векторана вектор, 4) уравнение прямойAB, 5) уравнение плоскостиABC,. Сделать чертеж.

А (3,5,4); В (5,8,3); С (1,9,9); D(6,4,8)