
- •Сахалинский государственный университет
- •Никитина Алла Борисовна, Чан Сун Нами
- •Программа курса «Математика»
- •Раздел 6. Дифференциальное исчисление функций
- •Раздел 7. Элементы интегрального исчисления
- •Раздел 8. Элементы теории рядов
- •Раздел 9. Элементы теории дифференциальных уравнений
- •Раздел 10. Элементы теории поля
- •1.2. Методические указания и решение типового варианта
- •Предел функции в точке
- •Дифференциал функции в точке
- •Основные теоремы дифференциального исчисления
- •Методы исследования функций и поведения их графиков.
- •Функция двух переменных
- •1.3. Вопросы для контроля
- •Раздел 2. Математический анализ
- •2.1. Методические указания и решение типового варианта контрольной работы № 3
- •2.2. Методические указания и решение типового варианта контрольной работы № 4 Элементы теории поля
- •2.3. Вопросы для контроля
- •Раздел 3. Теория вероятностей
- •3.1. Методические указания и решение типового варианта
- •Контрольная работа № 1 по теме: «Элементы векторной алгебры и аналитической геометрии»
- •Контрольная работа № 2
- •Контрольная работа № 3
- •Контрольная работа № 4
- •Контрольная работа № 5
- •Значение функции Пуассона
- •Список литературы
2.2. Методические указания и решение типового варианта контрольной работы № 4 Элементы теории поля
Основными понятиями являются: градиент, поток, потенциал, дивергенция, ротор, циркуляция.
Определение:Полем называется область некоторого пространства, в каждой точке которой определено значение некоторой величины.
Определение: Если каждой точке М областиVсоответствует определенное число=(М), то говорят, что в областиVзадано скалярное поле.
Определение:
Если каждой точке М из областиVсоответствует некоторый вектор![]() ,
то говорят, что задано векторное поле.
,
то говорят, что задано векторное поле.
Если функция (М)
(![]() )
не зависит от времени, то скалярное
(векторное) поле называется стационарным,
а поле, которое меняется с течением
времени, называется нестационарным.
)
не зависит от времени, то скалярное
(векторное) поле называется стационарным,
а поле, которое меняется с течением
времени, называется нестационарным.
В
трехмерном пространстве каждой точке
М области можно поставить в соответствие
либо ее координаты (х, y,
z),
либо радиус-вектор
![]() .
Следовательно, скалярное поле
можно задать как функцию трех переменных
(х, y,
z)
или как функцию одной переменной
(
.
Следовательно, скалярное поле
можно задать как функцию трех переменных
(х, y,
z)
или как функцию одной переменной
(![]() ).
).
Определение:Множество точек поля, в которых скаляримеет одно и то же значение, называется поверхностью уровня поля(х,y,z) = С, гдеC=const.
Так как функция поля однозначна, то через каждую точку поля М (х1,y1,z1) проходит единственная поверхность уровня(х,y,z) =( х1,y1,z1).
Пусть М – произвольная
точка пространства, где задано поле =(х,y,z). Производной функциив точке М в направлении любого вектора![]() называется предел отношения приращения=(М1)
–(М) кr,
приr0
(М1М), т. е.
называется предел отношения приращения=(М1)
–(М) кr,
приr0
(М1М), т. е.
![]() ,
обозначают
,
обозначают
![]() .
.
Производная
характеризует скорость изменения
функции (поля) в заданной точке М в
направлении вектора
![]() .
.
Если
![]() > 0, то функциявозрастает в направлении вектора
> 0, то функциявозрастает в направлении вектора![]() ,
если
,
если![]() < 0, то функцияубывает в направлении вектора
< 0, то функцияубывает в направлении вектора![]() .
.
![]()
–есть мгновенная
скорость функции в направлении вектора
–есть мгновенная
скорость функции в направлении вектора![]() .
.
![]() =
=![]() +
+![]() +
+![]() ,
где
,
где![]() ,
,![]() ,
,![]() – направляющие косинусы вектора
– направляющие косинусы вектора![]() .
.
Определение: Градиентом функции(х,y,z) обозначаютgrad, называют вектор, координатами которого являются значения частных производных функции(х,y,z) в точке М (х,y,z):
grad=![]() +
+![]() +
+![]() ,
где
,
где![]() ,
,![]() ,
,![]() – единичные векторы, илиgrad=(
– единичные векторы, илиgrad=(![]() ;
;![]() ;
;![]() ).
).
Направление градиента совпадает с направлением наибыстрейшего роста функции (поля), следовательно, наибольшая скорость изменения поля в точке М равна
grad=![]() .
.
Перечислим свойства градиента.
Теорема: Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
1) grad(u + v) = gradu + gradv,
2) grad(cu) = cgradu, c = const,
3) grad(uv) = u gradv + v gradu,
4) grad![]() =
=
![]() ,
,
5) gradF(u)
=
![]() .
.
Векторное поле
Определение:Векторной линией поля![]() называется линия, касательная к которой
в каждой ее точке М имеет направление
соответствующего ей вектора поля.
Совокупность всех векторных линий
поля, проходящих через некоторую
замкнутую кривую, называется векторной
трубкой.
называется линия, касательная к которой
в каждой ее точке М имеет направление
соответствующего ей вектора поля.
Совокупность всех векторных линий
поля, проходящих через некоторую
замкнутую кривую, называется векторной
трубкой.
Векторная линия
![]() описывается системой
описывается системой
![]() .
.
Пусть векторное
поле образовано вектором
![]() .
К понятию векторного поля приводит
физическая задача, изучающая поля
скоростей текущей жидкости. Некоторая
поверхностьzнаходится
в этом потоке и пропускает жидкость.
Найдем количество жидкости, протекающей
через поверхностьz.
Разобьем эту поверхность наnчастичных областей произвольным образомS1,S2,
... ,Sn
и выберем в каждой части области
некоторую точку Мi,
в которой построим единичный вектор
нормали
.
К понятию векторного поля приводит
физическая задача, изучающая поля
скоростей текущей жидкости. Некоторая
поверхностьzнаходится
в этом потоке и пропускает жидкость.
Найдем количество жидкости, протекающей
через поверхностьz.
Разобьем эту поверхность наnчастичных областей произвольным образомS1,S2,
... ,Sn
и выберем в каждой части области
некоторую точку Мi,
в которой построим единичный вектор
нормали![]() .
За единицу времени черезSiпротекает количество жидкости, приближенно
равное
.
За единицу времени черезSiпротекает количество жидкости, приближенно
равное![]() ,
где
,
где![]() – высотаi-того цилиндра,
а
– высотаi-того цилиндра,
а![]() – площадьi-той площади.
Но
– площадьi-той площади.
Но![]() является проекцией вектора
является проекцией вектора![]() на нормаль
на нормаль![]() :
:![]() ,
следовательно, общий объем жидкости,
протекающий через поверхностьSза единицу времени, равен приближенно:
,
следовательно, общий объем жидкости,
протекающий через поверхностьSза единицу времени, равен приближенно:![]() .
Точное значение этой величины получим,
перейдя к пределу при неограниченном
увеличении числа частичных площадок.
Если
.
Точное значение этой величины получим,
перейдя к пределу при неограниченном
увеличении числа частичных площадок.
Если![]() – диаметр площади, то
– диаметр площади, то
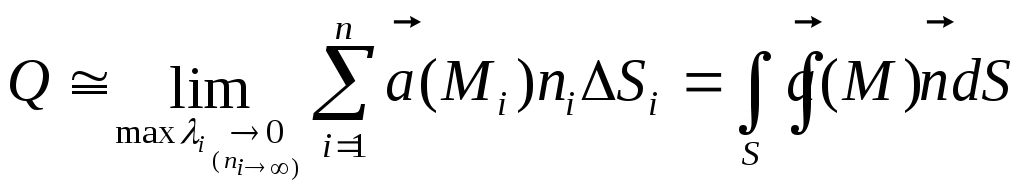 .
.
Определение:
Предел суммы элементарных потоков
через частичные области, на которые
разбивается областьS,
когда число частичных областей
неограниченно растет при условии, что
наибольший из диаметров площади
неограниченно убывает, называется
потоком векторного поля![]() через поверхностьS.
через поверхностьS.
Определение:Потоком вектора![]() через поверхностьSназывается интеграл по поверхности от
скалярного произведения вектора поля
на единичный вектор нормали к поверхности
через поверхностьSназывается интеграл по поверхности от
скалярного произведения вектора поля
на единичный вектор нормали к поверхности
![]() или
или
![]() .
.
Замечание. Поток
вектора![]() есть величина скалярная, равная объему
жидкости, протекающей через поверхностьSза единицу времени.
есть величина скалярная, равная объему
жидкости, протекающей через поверхностьSза единицу времени.
Если поверхность
замкнута и ограничивает некоторый
объем, то
![]() ,
в этом случае за направление вектора
,
в этом случае за направление вектора![]() берут направление внешней нормали и
говорят о потоке изнутри. Так как
берут направление внешней нормали и
говорят о потоке изнутри. Так как![]() ,
то
,
то![]() .
.
Дивергенция векторного поля
Определение:
Дивергенцией векторного поля![]() в точке М называется скаляр вектора
вида
в точке М называется скаляр вектора
вида![]() и обозначаютdiv
и обозначаютdiv![]()
div![]() (M)
=
(M)
=![]() .
.
Свойства дивергенции:
div
 = 0, если
= 0, если – постоянный вектор,
– постоянный вектор,div
 = сdiv
= сdiv ,
где с =const,
,
где с =const,div
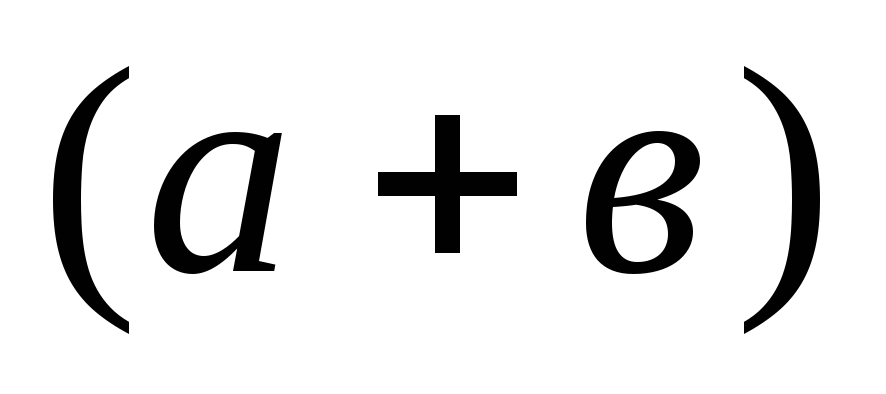 =
div
=
div +
div
+
div ,
,div
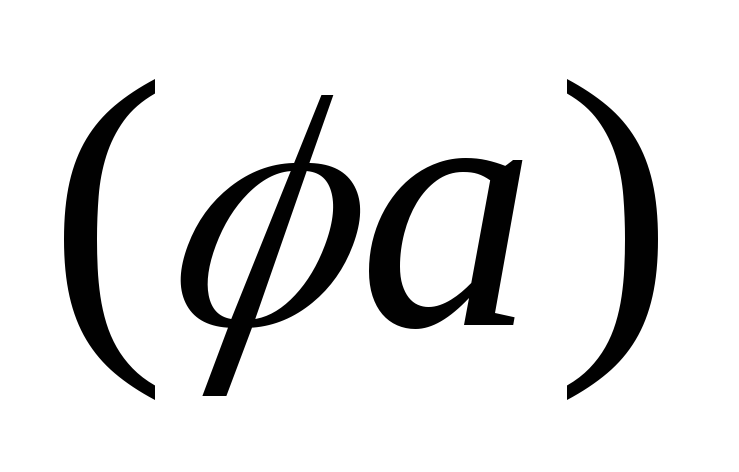 =
=
 div
div +
+ div
div ,
если
,
если – скалярная функция.
– скалярная функция.
Замечание.Формула Остроградского – Гаусса, с использованием понятий потока и дивергенции векторного поля, запишется так:
![]() =
=
![]()
![]() .
.
Формула Остроградского – Гаусса показывает, что поток векторного поля через замкнутую поверхность S(в направлении векторной нормали) равен тройному интегралу от дивергенции этого поля по объемуV, ограниченного данной поверхностью.
![]() =
=![]()
![]() ,
по теореме о среднем для тройного
интеграла имеем:
,
по теореме о среднем для тройного
интеграла имеем:![]()
![]()
![]()
![]() ,
при
,
при![]() получим
получим![]()
![]() .
.
Определение: Дивергенцией векторного поля в точке М называется предел отношения потока поля через поверхностьS, окружающую точку М, к объему тела, ограниченного этой поверхностью, при условии, что поверхность стягивается в точку М.
Циркуляция и вихрь векторного поля
Рассмотрим в поле
![]() линиюLи выберем на ней
направление. Для произвольной точки М
кривой запишем радиус-вектор
линиюLи выберем на ней
направление. Для произвольной точки М
кривой запишем радиус-вектор![]() ,
вектор
,
вектор![]() будет направлен по касательной к кривой
в направлении ее обхода
будет направлен по касательной к кривой
в направлении ее обхода![]() .
.
Определение:
Циркуляцией
вектора
![]() вдоль кривойL
называется криволинейный интеграл по
замкнутому контуру L
от скалярного произведения вектора
вдоль кривойL
называется криволинейный интеграл по
замкнутому контуру L
от скалярного произведения вектора
![]() на
на![]() (касательный кL)
(касательный кL)
![]() ,
,
или,
учитывая, что
![]() ,
получим
,
получим![]() ,
где
,
где![]() – проекция вектора
– проекция вектора![]() на касательную
на касательную![]() ,
проведенную в направлении обхода.
,
проведенную в направлении обхода.
Физический смысл
циркуляции состоит в том, что если кривая
Lрасположена в силовом
поле, то циркуляция – это работа силы![]() поля при перемещении материальной точки
вдольL.
поля при перемещении материальной точки
вдольL.
Замечание.
Циркуляция отлична от нуля вдоль
замкнутой линии, так как в каждой точке
векторной линии![]() сохраняет значение: положительное, если
направление
сохраняет значение: положительное, если
направление![]() совпадает с направлением обхода линии;
отрицательное – в противоположном
случае.
совпадает с направлением обхода линии;
отрицательное – в противоположном
случае.
Определение:
Вихревым вектором или ротором
векторного поля![]() называется вектор, определяемый
равенством
называется вектор, определяемый
равенством![]() .
.
Или
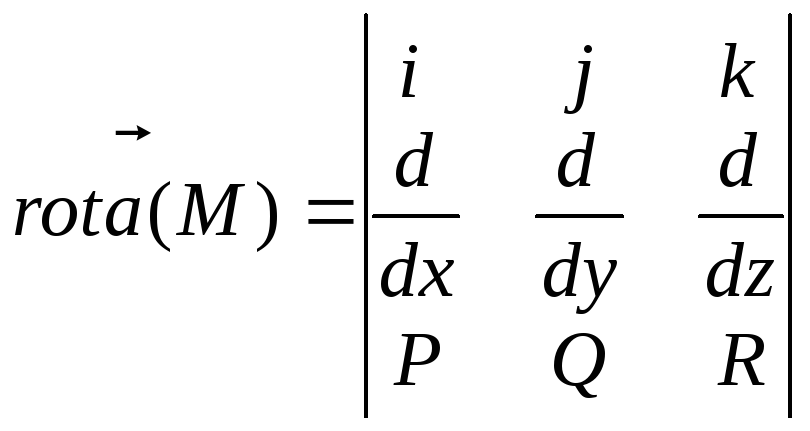 .
.
Свойства ротора:
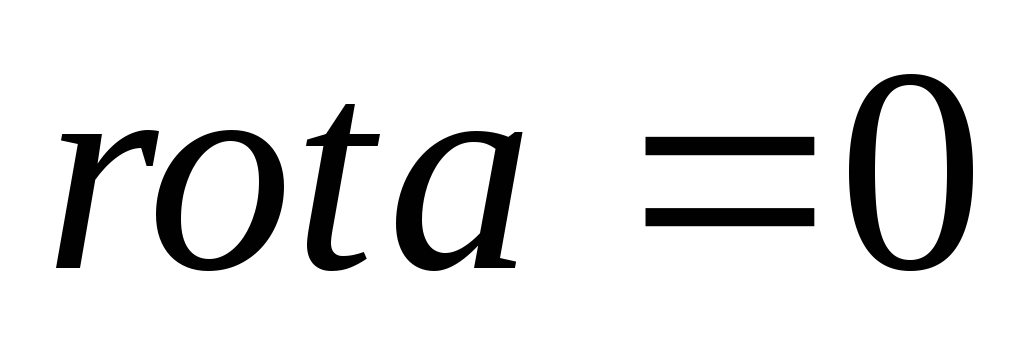 ,
если
,
если
 – постоянный вектор,
– постоянный вектор,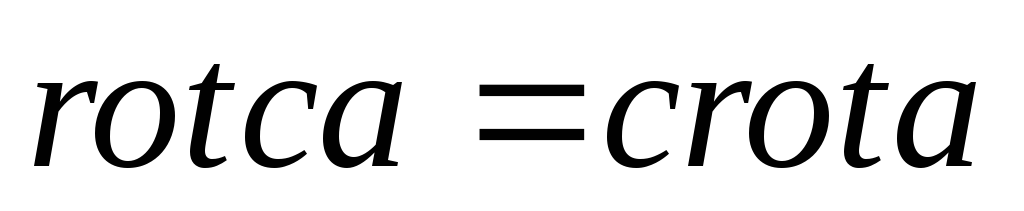 ,
где с = const,
,
где с = const,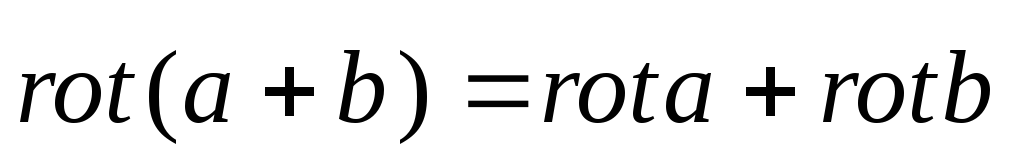 ,
, ,
где
,
где
 – скалярная функция.
– скалярная функция.
Формула Стокса примет вид:
![]() –это векторная
форма формулы, которая показывает, что
циркуляция вектора
–это векторная
форма формулы, которая показывает, что
циркуляция вектора
![]() вдоль замкнутого контураLравна потоку ротора этого вектора
вдоль замкнутого контураLравна потоку ротора этого вектора![]() через поверхностьS,
лежащую в поле вектора
через поверхностьS,
лежащую в поле вектора![]() и ограниченную контуромL.
и ограниченную контуромL.
Так как
![]() по теореме о среднем, то
по теореме о среднем, то![]() .
.
Если контур Lстягивается в точку М, то![]() и
и![]() .
.
Замечание.Направление ротора – это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадкеS. Поэтому связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению.
Оператор Гамильтона
Определение: Векторными операциями первого порядка называется взятие градиента, дивергенции и ротора.
Оператор Гамильтона (символический вектор) имеет вид:
![]() .
.
С помощью оператора Гамильтона основные дифференциальные операции можно записать так:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Задача.Вычислить координаты центра масс
однородного тела, ограниченного
поверхностями:![]()
Решение: Данное тело симметрично относительно оси ОY, поэтомуxc =zc = 0 (т. е. центр симметрии находится на оси ОY). Ордината центра масс найдется по формуле:
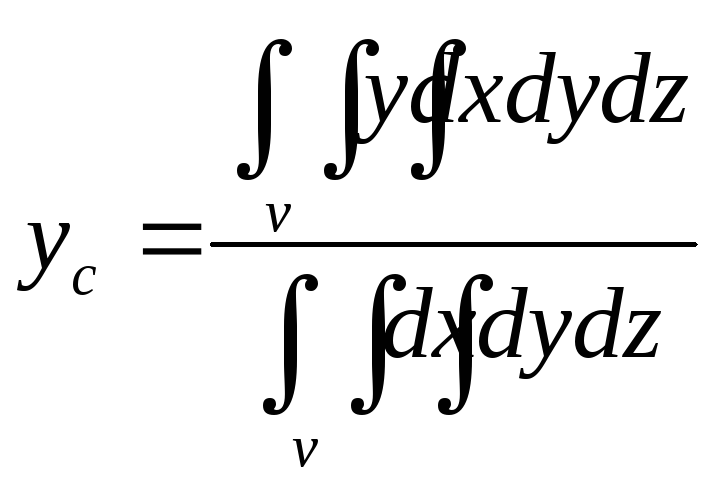 .
.
Перейдем к
цилиндрическим координатам:
![]() ,
,![]() ,
,![]() ,
тогда
,
тогда
1)
![]() .
Для нахождения пределов интегрирования
найдем проекцию области на плоскостьOXZ, получим
.
Для нахождения пределов интегрирования
найдем проекцию области на плоскостьOXZ, получим![]() ,
следовательно,
,
следовательно,![]() ,
,![]() ,
,![]() .
Получим кратный интеграл
.
Получим кратный интеграл
![]() =
=
![]() =
16;
=
16;
2)
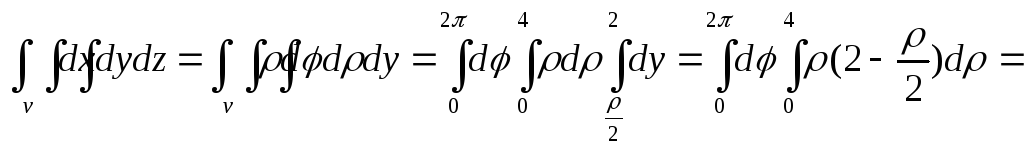
![]() = =
= =![]() ;
;
3)
![]() .
.
Итак, центр масс
С (0;
![]() ;
0).
;
0).
Задача. Вычислить производную функцииZ=arctg(хy) в точке М0 (1,1) вдоль кривой у = х2, в положительном направлении оси ОХ.
Решение:Если
функцияu=f(x,y,z)
определена в окрестности точки М (х0,
у0,z0), то
производная функции по направлению
вектора![]() определяется по формуле:
определяется по формуле:
![]()
где
![]() – направляющие косинусы вектора
– направляющие косинусы вектора![]() .
.
Производной вдоль кривой Lназывают производную по направлению ориентированной касательной к кривой, вычисленную в точке касания.
За направление параболы у = х2 в точке М0 (1,1) возьмем направление касательной к параболе в этой точке, задаваемой углом, который касательная образует с осью ОХ. Тогда
![]() так как
так как
![]() и
и![]() ,
то
,
то
![]() ;
;
![]() .
.
Найдем частные производные функции, U=arctg(xy), в точке М (1,1):
![]() ;
;
![]()
![]() .
.
Поверхностный интеграл первого рода определяется равенством
![]() при условии
существования предела, где Si– элемент поверхностиS,Si
– диаметр частичных поверхностей,
при условии
существования предела, где Si– элемент поверхностиS,Si
– диаметр частичных поверхностей,![]() Si
– площади частичных поверхностей.
Для вычисления поверхностного интеграла
применим формулу:
Si
– площади частичных поверхностей.
Для вычисления поверхностного интеграла
применим формулу:![]() гдеD– проекция поверхностиSна плоскости ОХУ является
однозначной, тогдаF(x,y) =Z–
уравнение поверхности.
гдеD– проекция поверхностиSна плоскости ОХУ является
однозначной, тогдаF(x,y) =Z–
уравнение поверхности.
Задача.Вычислить![]() ,
гдеS– часть конической
поверхности х2 + у2 =z2,
расположенной между плоскостямиZ= 0 иZ= 2.
,
гдеS– часть конической
поверхности х2 + у2 =z2,
расположенной между плоскостямиZ= 0 иZ= 2.
Решение:Из
уравнения поверхности находим![]() ,
при 0
,
при 0![]() Z
Z
![]() 2; проекцией этой поверхности на плоскость
ОХYявляется круг х2 +
у2
2; проекцией этой поверхности на плоскость
ОХYявляется круг х2 +
у2 ![]() 4.
4.
![]()
![]()
![]() ;
;
Z





Y





2
2
X
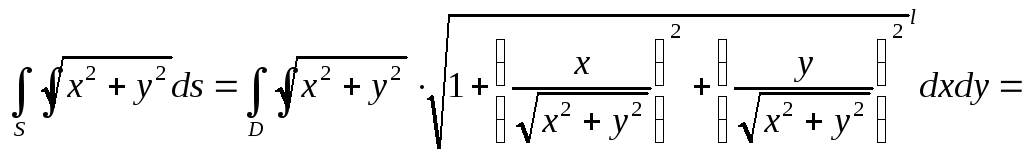
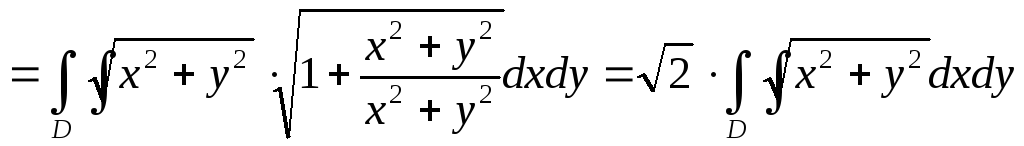 .
.
Перейдем к полярным
координатам
![]() ,
получим:
,
получим:
![]() .
.
Если S – гладкая замкнутая поверхность, ограничивающая V и Р = Р (х, у, z), Q = Q (x, y, z),R=R(x,y,z) – непрерывные функции вместе со своими частными производными первого порядка, то имеет место формула Остроградского – Гаусса:
![]()
или
![]() (*)
(*)
Задача.Вычислить:![]() ,
еслиS– поверхность,
ограниченная плоскостямиx= 0,y= 0,z=
0,x+ 2y+ 3z= 6.
,
еслиS– поверхность,
ограниченная плоскостямиx= 0,y= 0,z=
0,x+ 2y+ 3z= 6.
По
формуле Остроградского – Гаусса имеем:
![]() ,
так какP(x,
y,
z)
= x
+ yи
,
так какP(x,
y,
z)
= x
+ yи![]() ,Q(x,y,z) =y+zи
,Q(x,y,z) =y+zи![]() ,R(x,y,z)=z+xи
,R(x,y,z)=z+xи![]() ,
следовательно,
,
следовательно,![]() ,
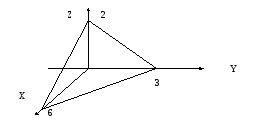
геометрически последний интеграл
выражает объем областиV(тетраэдра), ограниченный координатными
плоскостями и плоскостью х + 2у + 3z= 6, или в отрезках уравнение плоскости
имеет вид:
,
геометрически последний интеграл
выражает объем областиV(тетраэдра), ограниченный координатными
плоскостями и плоскостью х + 2у + 3z= 6, или в отрезках уравнение плоскости
имеет вид:![]() .
.
Задача.Вычислить поток векторного поля![]() через верхнюю часть плоскости х + 2у + 3z– 6 = 0, расположенной в первом октанте.
через верхнюю часть плоскости х + 2у + 3z– 6 = 0, расположенной в первом октанте.
Решение:ВыразимZиз уравнения плоскости:![]() ,
тогда
,
тогда![]() .
.
Вычислим поток,
пользуясь формулой
![]()
![]()
![]() =
=![]()
Так как проекцией
плоскости х + 2у + 3z– 6 = 0
на плоскости ОХYявляется
треугольник, ограниченный прямыми у =
0, х = 0 и х + 2у = 6, то 0![]() (см. рисунок), то
(см. рисунок), то
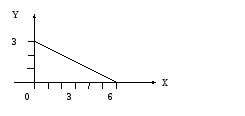
![]()
Задача. Вычислить дивергенцию векторного поля
![]() в точке М0(1,
–2, 3).
в точке М0(1,
–2, 3).
Решение:
![]()
![]()
Так как
![]() ,
то точка М0является источником
поля.
,
то точка М0является источником
поля.
