
- •Сахалинский государственный университет
- •Никитина Алла Борисовна, Чан Сун Нами
- •Программа курса «Математика»
- •Раздел 6. Дифференциальное исчисление функций
- •Раздел 7. Элементы интегрального исчисления
- •Раздел 8. Элементы теории рядов
- •Раздел 9. Элементы теории дифференциальных уравнений
- •Раздел 10. Элементы теории поля
- •1.2. Методические указания и решение типового варианта
- •Предел функции в точке
- •Дифференциал функции в точке
- •Основные теоремы дифференциального исчисления
- •Методы исследования функций и поведения их графиков.
- •Функция двух переменных
- •1.3. Вопросы для контроля
- •Раздел 2. Математический анализ
- •2.1. Методические указания и решение типового варианта контрольной работы № 3
- •2.2. Методические указания и решение типового варианта контрольной работы № 4 Элементы теории поля
- •2.3. Вопросы для контроля
- •Раздел 3. Теория вероятностей
- •3.1. Методические указания и решение типового варианта
- •Контрольная работа № 1 по теме: «Элементы векторной алгебры и аналитической геометрии»
- •Контрольная работа № 2
- •Контрольная работа № 3
- •Контрольная работа № 4
- •Контрольная работа № 5
- •Значение функции Пуассона
- •Список литературы
1.2. Методические указания и решение типового варианта
контрольной работы № 2
Предел функции в точке
Определение:Последовательностью называется функция
натурального аргумента![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,
,…,![]() ,…
. Причем если
,…
. Причем если![]() ,
то
,
то![]() следует
за
следует
за![]() ,
независимо от того, больше он его или
меньше.
,
независимо от того, больше он его или
меньше.
Последовательность
чисел называется сходящейся к числу
![]() ,
если для любого положительного, сколь
угодно малого числа
,
если для любого положительного, сколь
угодно малого числа![]() (эпсилон) найдется такой номер
(эпсилон) найдется такой номер![]() ,
что для всех номеров
,
что для всех номеров![]() будет
выполняться неравенство
будет
выполняться неравенство![]() .
Пишут
.
Пишут
![]() .
.
Геометрический
смысл предела последовательности
состоит в том, что за пределами
![]() – окрестности точки
– окрестности точки![]() находится лишь конечное число членов
последовательности
находится лишь конечное число членов
последовательности![]() ,
а внутри этой окрестности находится
бесконечное множество членов
последовательности и при
,
а внутри этой окрестности находится
бесконечное множество членов
последовательности и при![]() число
число![]() будет сгустком точек, соответствующих
членам последовательности.
будет сгустком точек, соответствующих
членам последовательности.
Определение:Число![]() называется пределом функции
называется пределом функции![]() в точке
в точке![]() ,
если для любого
,
если для любого![]() сколь угодно малого положительного
числа
сколь угодно малого положительного
числа![]() найдется
найдется![]() положительное число
положительное число![]() (дельта),
что для всех
(дельта),
что для всех![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству![]() ,
выполнится неравенство
,
выполнится неравенство![]() .
.
Пишут
![]() .
.
Теоремы о пределах
функций: если существует
![]() и
и![]() ,
то
,
то
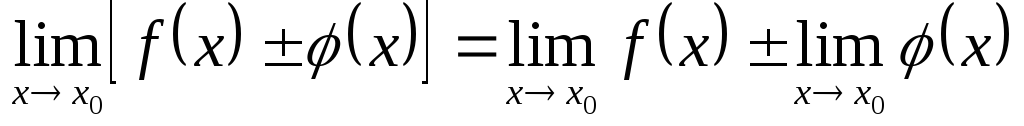 ;
;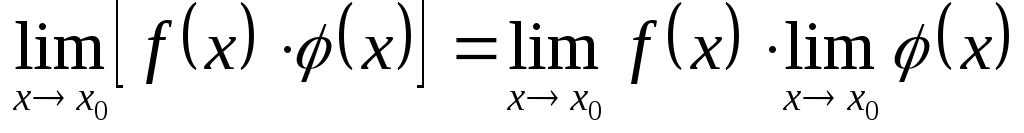 ;
; ;
;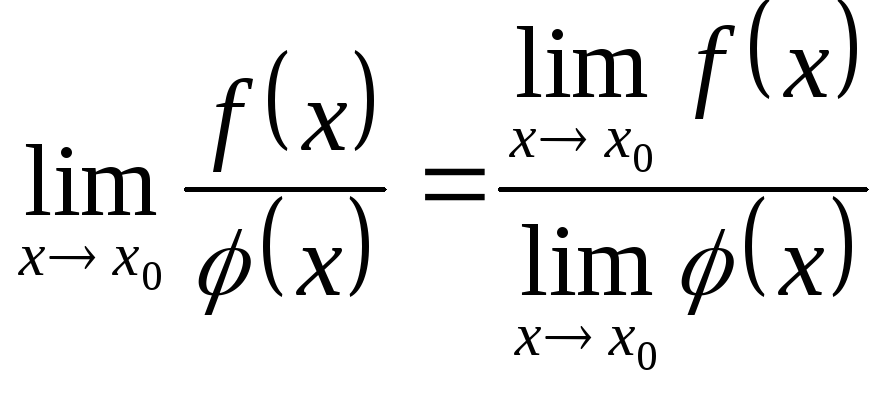 при
при
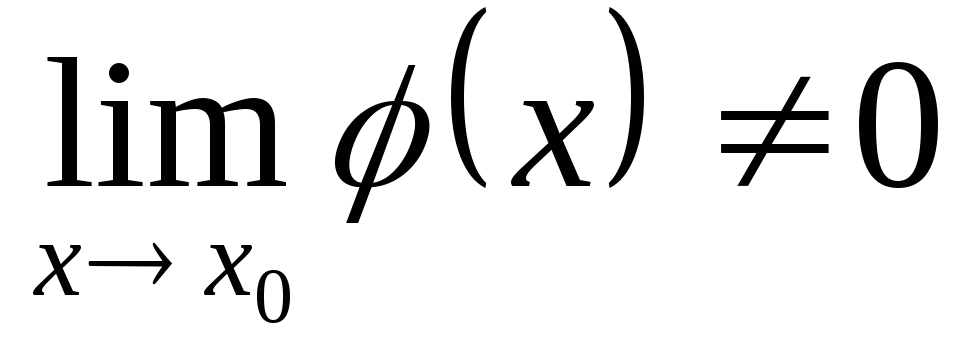 .
.
При вычислении пределов используются два замечательных предела:
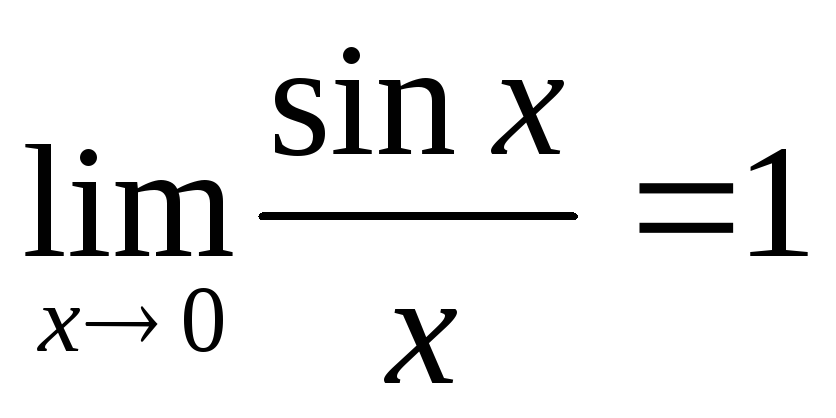 (первый замечательный
предел);
(первый замечательный
предел);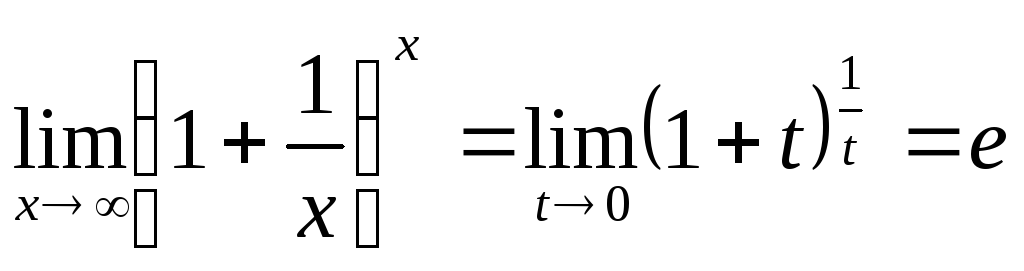 (второй
замечательный предел).
(второй
замечательный предел).
Определение:Функция![]() называется бесконечно малой в точке
называется бесконечно малой в точке![]() ,
если
,
если![]() .
.
Определение:Функция![]() называется бесконечно большой в точке
называется бесконечно большой в точке![]() ,
если
,
если![]() .
.
Теорема:Если![]() – бесконечно большая функция, то
– бесконечно большая функция, то![]() – бесконечно малая функция. Если
– бесконечно малая функция. Если![]() – бесконечно малая и
– бесконечно малая и![]() – бесконечно малая функция в точке
– бесконечно малая функция в точке![]() и
и![]() ,
то
,
то![]() и
и![]() эквивалентны. Пишут
эквивалентны. Пишут![]() ~
~![]() .
.
Примеры.Найти пределы функций, не пользуясь правилом Лопиталя:
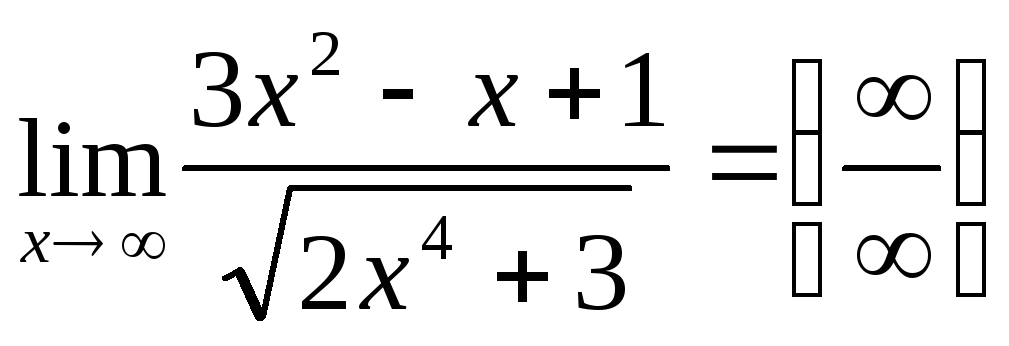 .
Разделим числитель и знаменатель на
высшую степень х, т. е. на
.
Разделим числитель и знаменатель на
высшую степень х, т. е. на
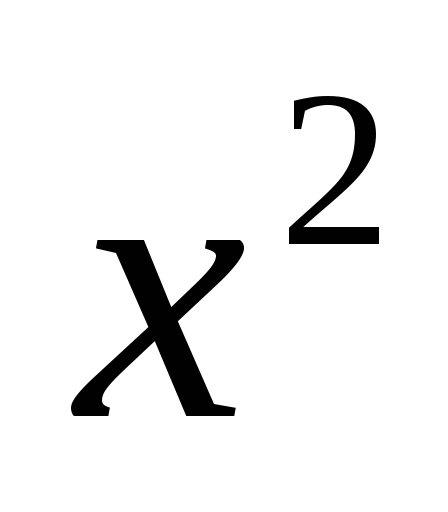 ,
,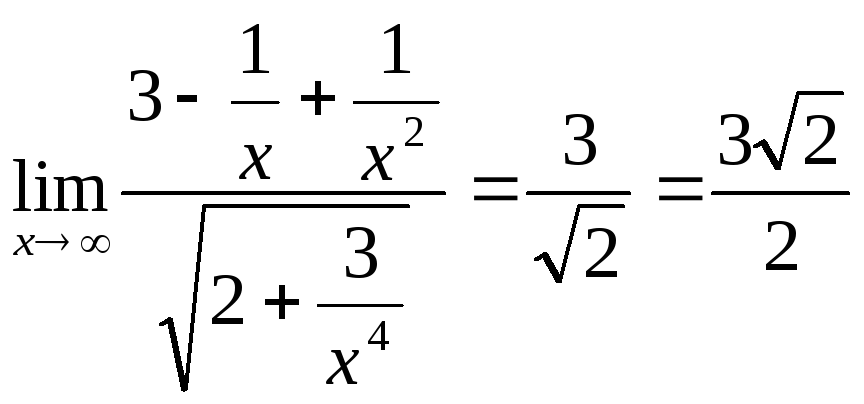 ;
;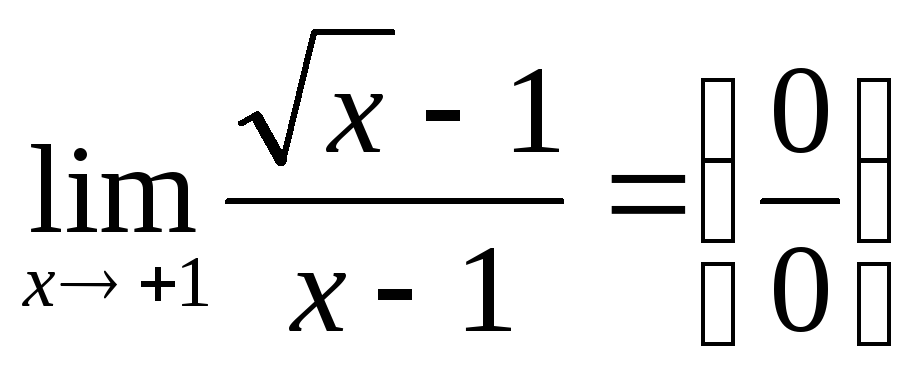 .
Выделим в знаменателе дроби критический
множитель
.
Выделим в знаменателе дроби критический
множитель
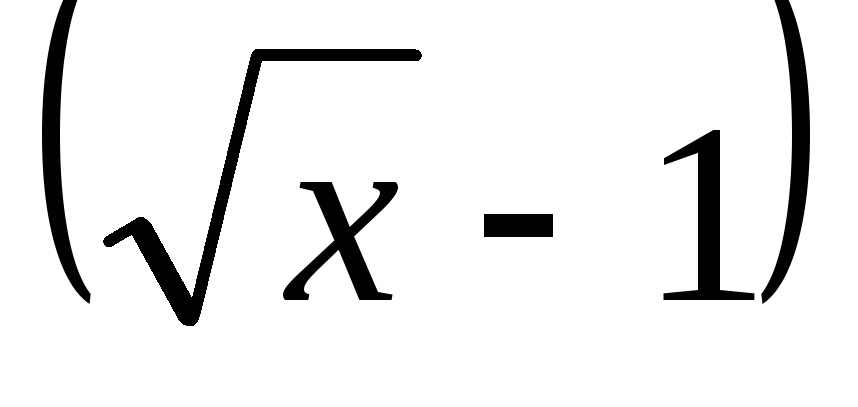 :
: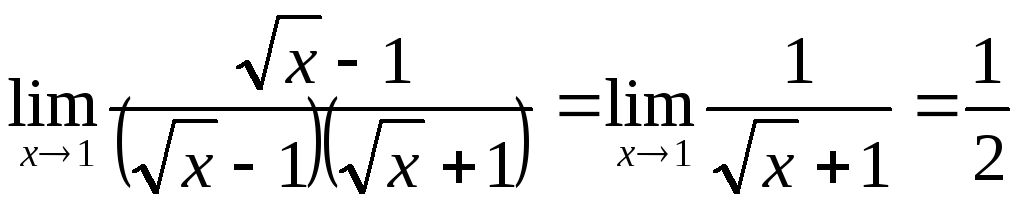 ;
;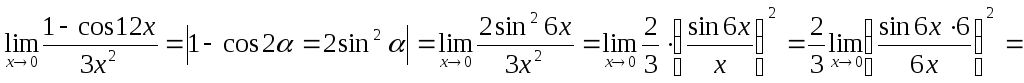
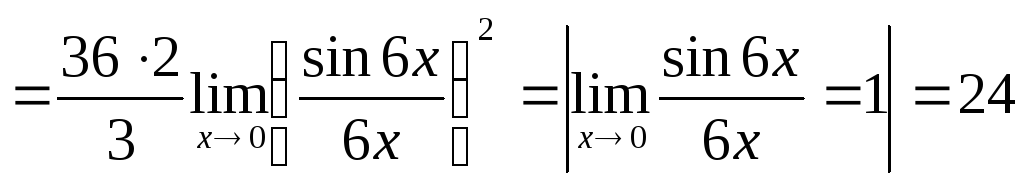 ;
;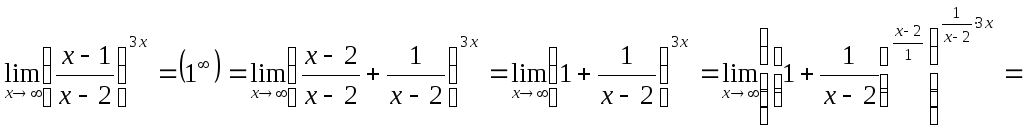
=
![]() .
.
Определение:Функция![]() называется непрерывной в точке
называется непрерывной в точке![]() ,
если существует предел функции в точке
,
если существует предел функции в точке![]() ,
равный значению функции в точке
,
равный значению функции в точке![]() ,
т. е.
,
т. е.![]() .
.
Иными словами,
функция непрерывна в точке
![]() ,
если выполняются равенства:
,
если выполняются равенства:
![]() (*)
(*)
Односторонние
пределы функции в точке
![]() равны значению функции в точке
равны значению функции в точке![]() .
.
Определение:Точка![]() называется точкой разрыва первого
рода, если существуют конечные, но
неравные односторонние пределы функции
в точке
называется точкой разрыва первого
рода, если существуют конечные, но
неравные односторонние пределы функции
в точке![]() .
Разность между правым и левым пределами
называется скачком.
.
Разность между правым и левым пределами
называется скачком.
Определение:Точка![]() называется точкой разрыва второго рода,
если хотя бы один из односторонних
пределов равен
называется точкой разрыва второго рода,
если хотя бы один из односторонних
пределов равен![]() или не существует.
или не существует.
Определение:Точка![]() называется
точкой разрыва устранимого, если
существует предел функции в этой точке,
не равный значению функции в точке
называется
точкой разрыва устранимого, если
существует предел функции в этой точке,
не равный значению функции в точке![]() .
.
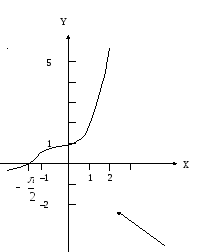
Пример.Исследовать функцию на непрерывность и построить график:
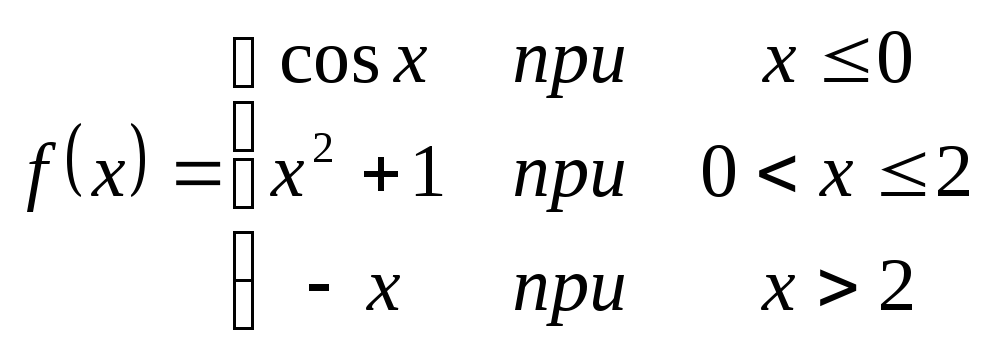 .
.
Решение:Функция![]() является непрерывной на каждом из
промежутков, поэтому подозрительными
на разрыв являются точки
является непрерывной на каждом из
промежутков, поэтому подозрительными
на разрыв являются точки![]() и
и![]() .
Исследуем каждую точку.
.
Исследуем каждую точку.
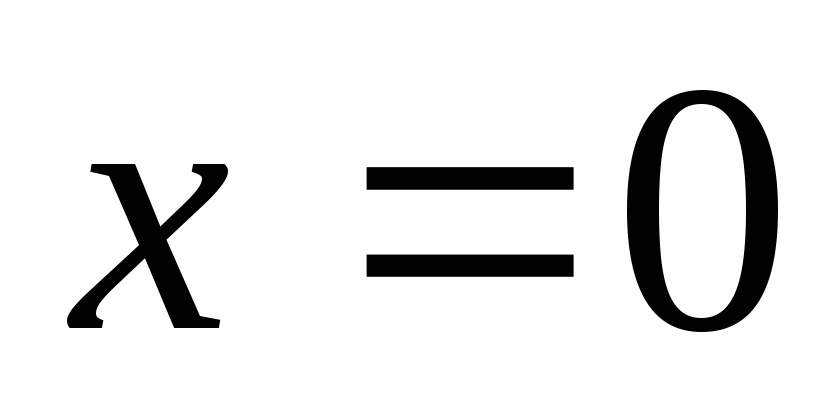 .
Найдем левосторонний и правосторонний
пределы функции
.
Найдем левосторонний и правосторонний
пределы функции
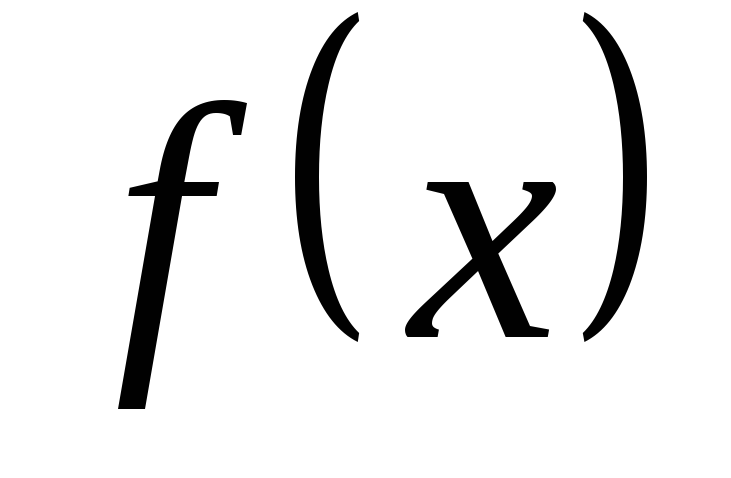 при
при
![]()
![]() ,
,
значение
функции в точке
![]() равно:
равно:![]() .
Следовательно, в точке
.
Следовательно, в точке![]() функция является непрерывной, так как
функция является непрерывной, так как
![]() .
.
![]()
![]() .
.
Так как односторонние
пределы конечны, но не равны, то точка
![]() является точкой разрыва первого рода.
является точкой разрыва первого рода.
Скачок равен
![]() .
.
Определение:Пусть функция![]() задана на некотором множестве
задана на некотором множестве![]() .
Зафиксируем значение аргумента
.
Зафиксируем значение аргумента![]() и придадим ему приращение
и придадим ему приращение![]() ,
не выводящее значение аргумента за
пределы множества
,
не выводящее значение аргумента за
пределы множества![]() ,
т. е.
,
т. е.![]() .
Тогда соответствующее приращение
.
Тогда соответствующее приращение![]() получит и сама функция, которое равно
разности нового и старого значений
функции:
получит и сама функция, которое равно
разности нового и старого значений
функции:![]() .
Если существует конечный предел отношения
приращения функции к приращению аргумента
при
.
Если существует конечный предел отношения
приращения функции к приращению аргумента
при![]() ,
то он называется производной функции
в точке
,
то он называется производной функции
в точке![]() .
Пишут
.
Пишут![]() ,
или
,
или![]() .
(6)
.
(6)
Если
![]() существует во всех точках множества
существует во всех точках множества![]() ,
то
,
то![]() является функцией от
является функцией от![]() .
.
Таблица производных основных элементарных функций
Если
![]() является дифференцируемой, то выполняются
равенства:
является дифференцируемой, то выполняются
равенства:
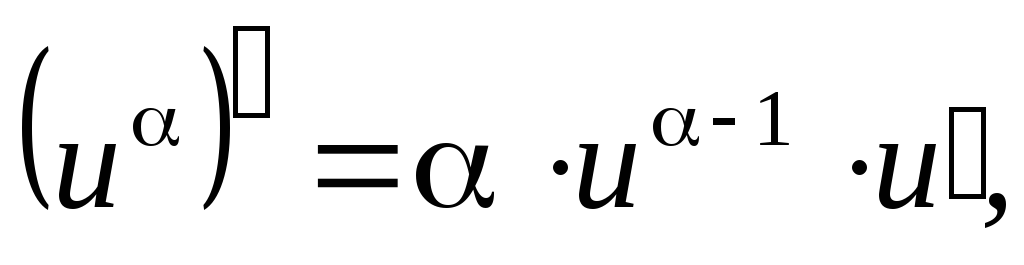 где
где
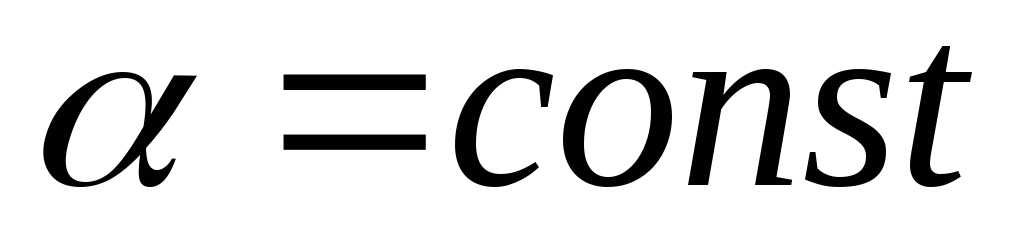
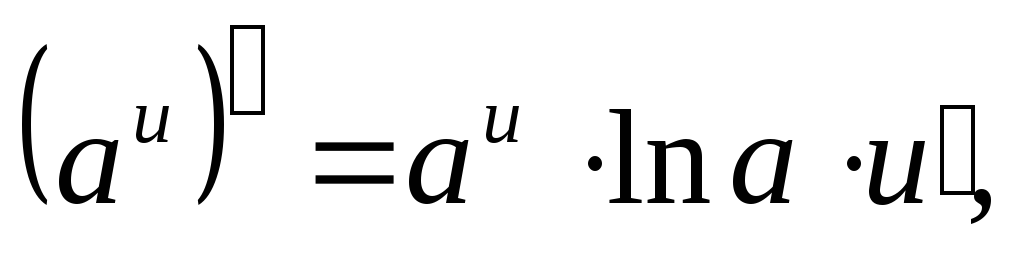 где
где
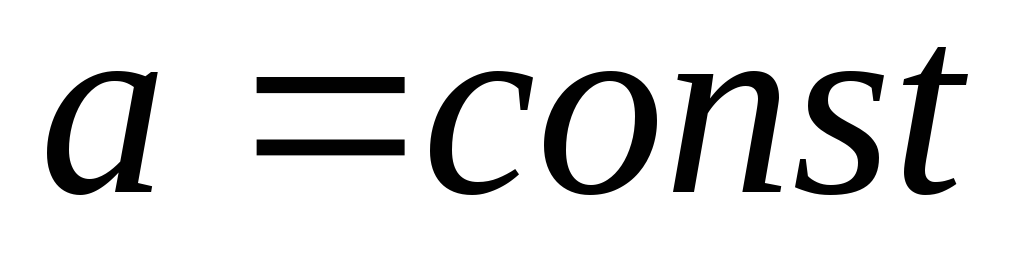
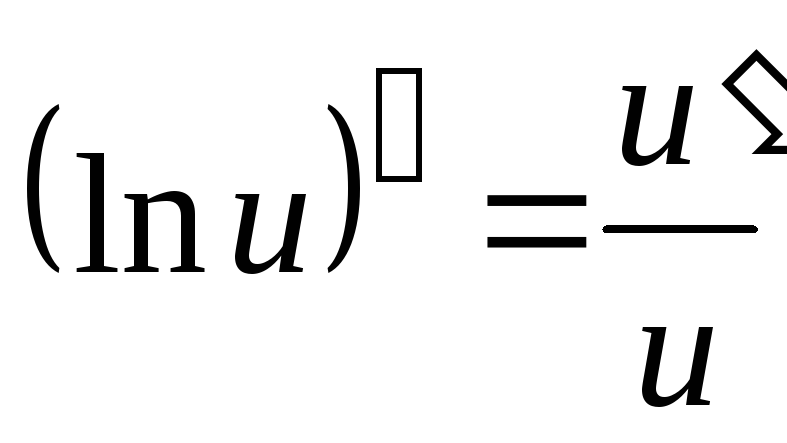
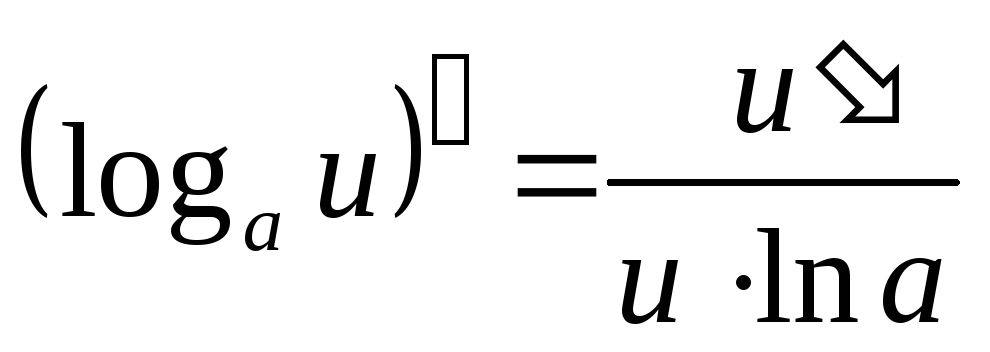
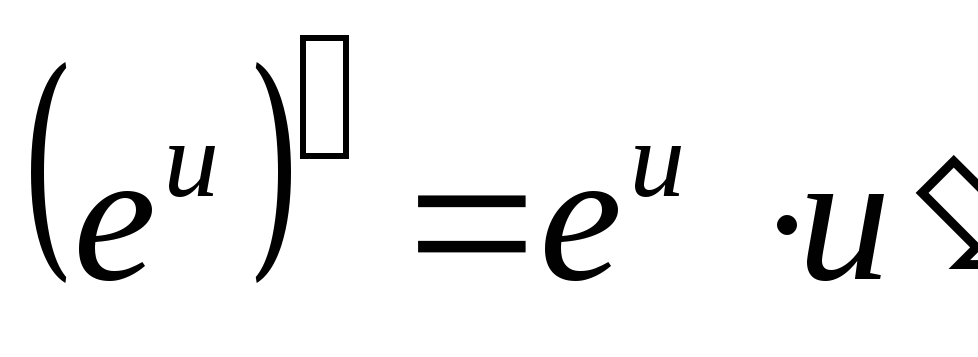
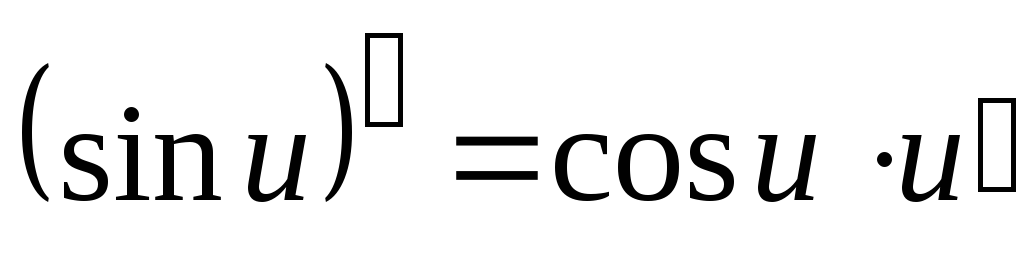
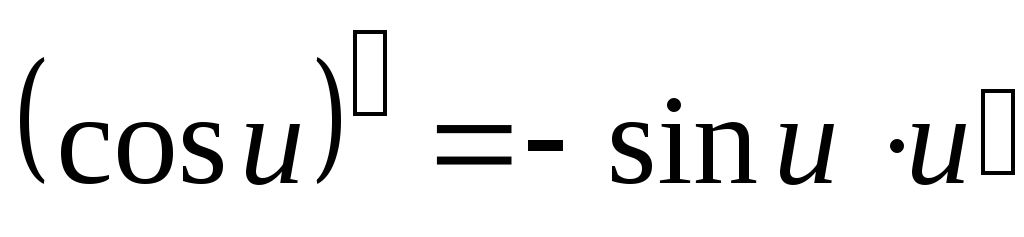
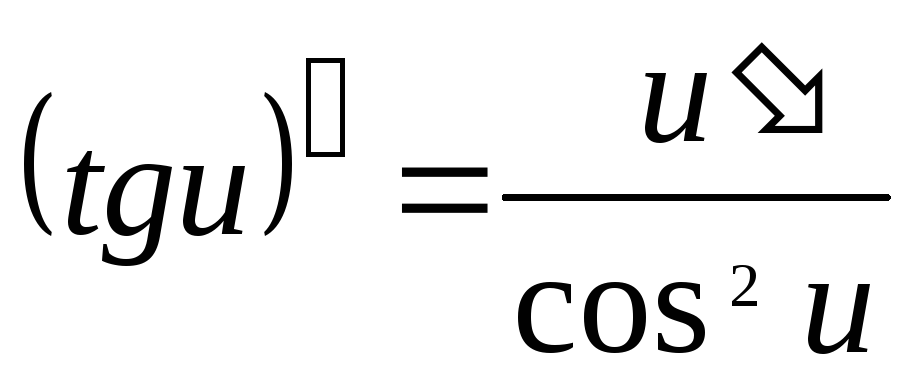
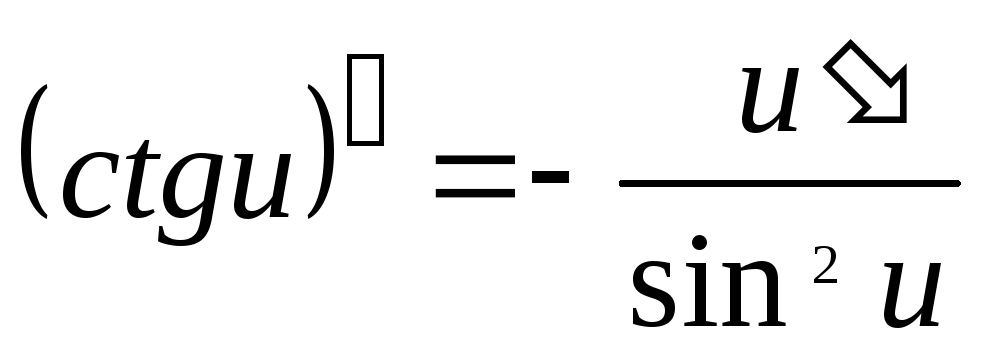
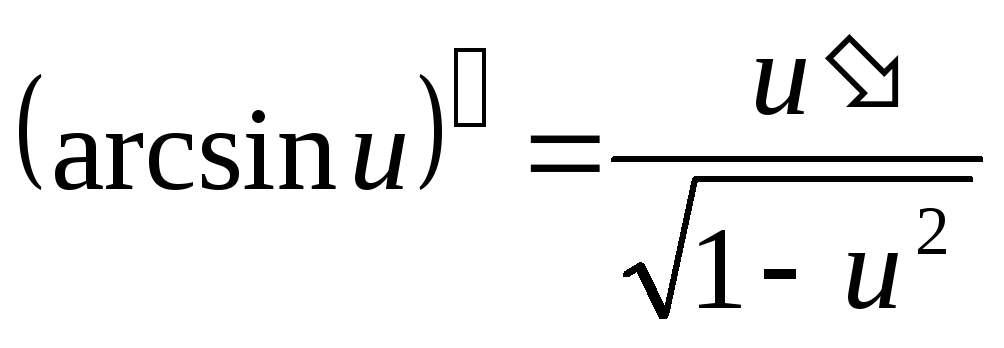
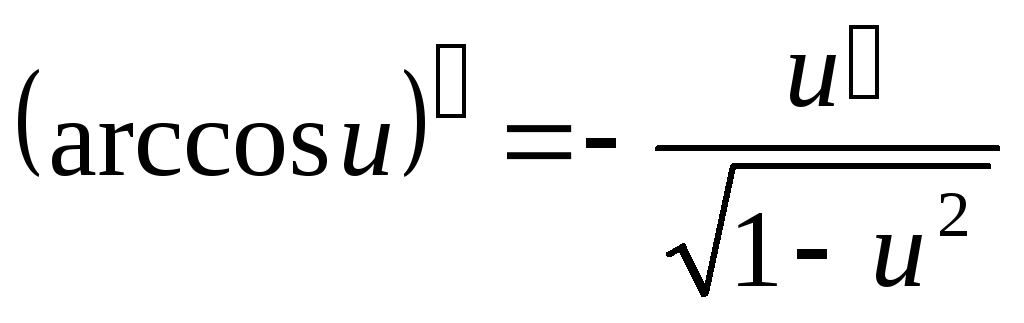
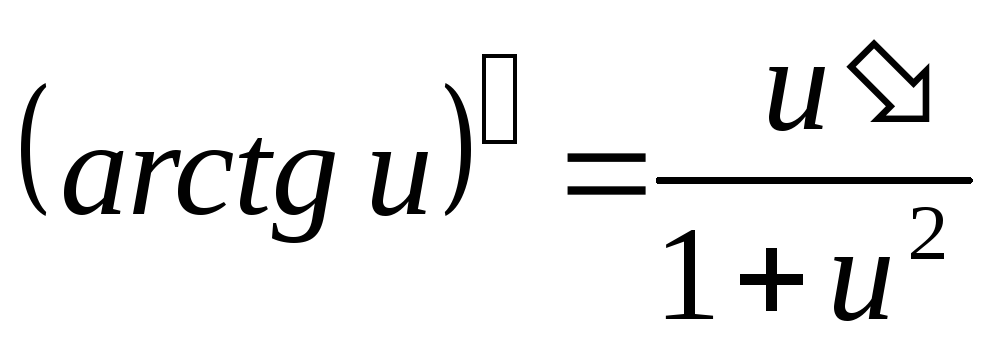
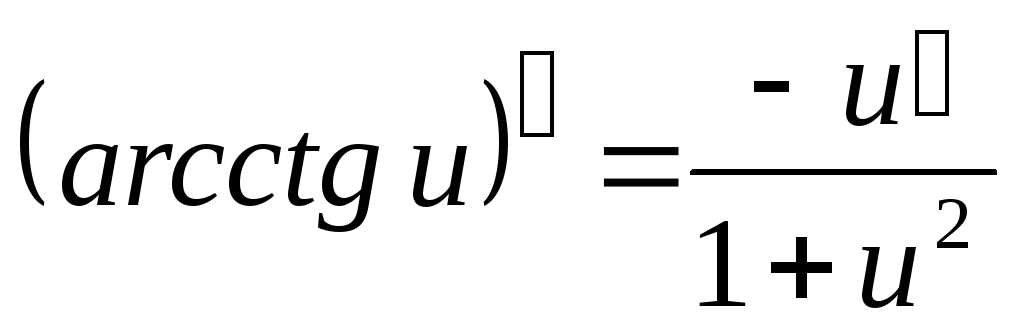
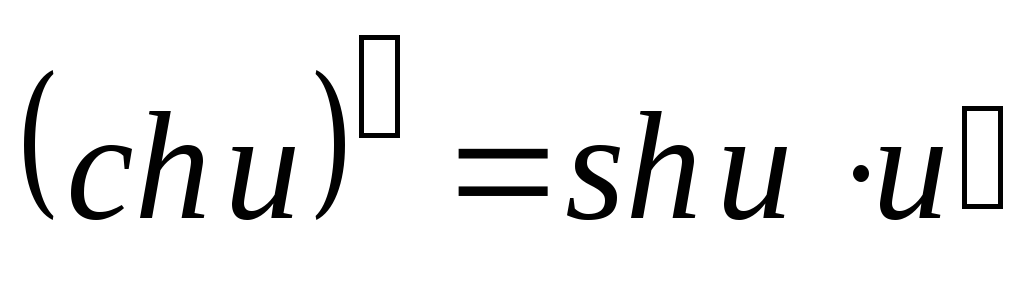
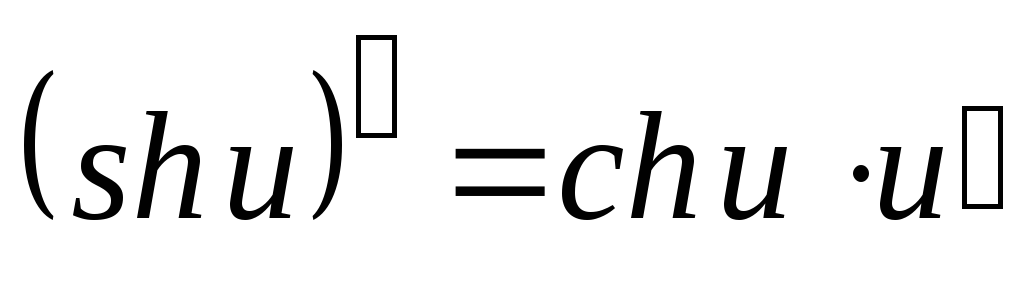
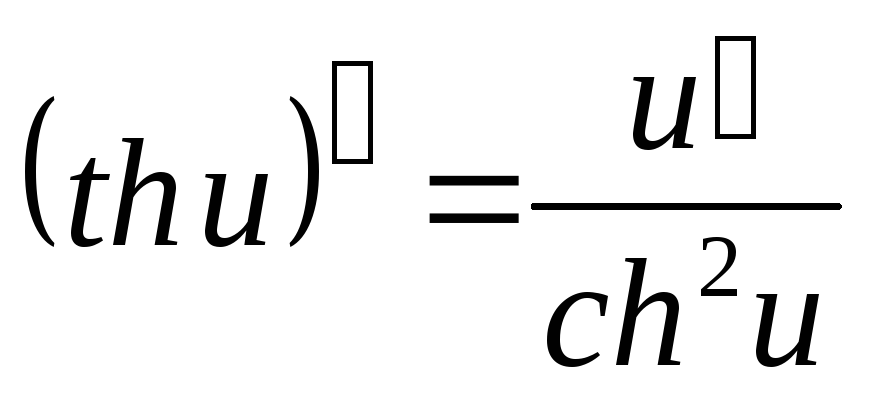
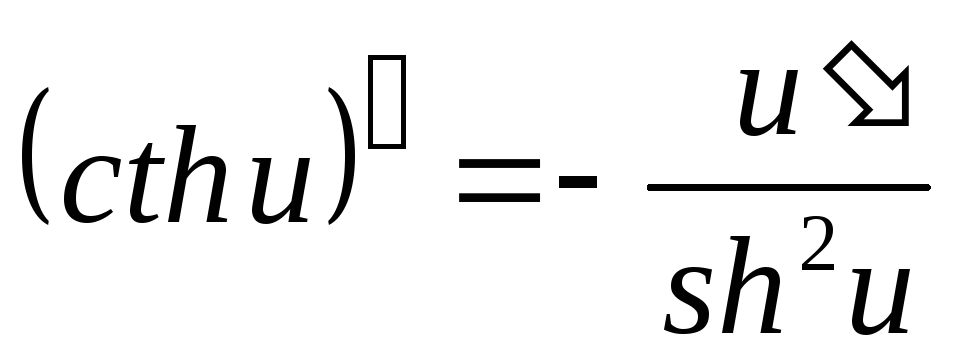 .
.
Основные правила дифференцирования:
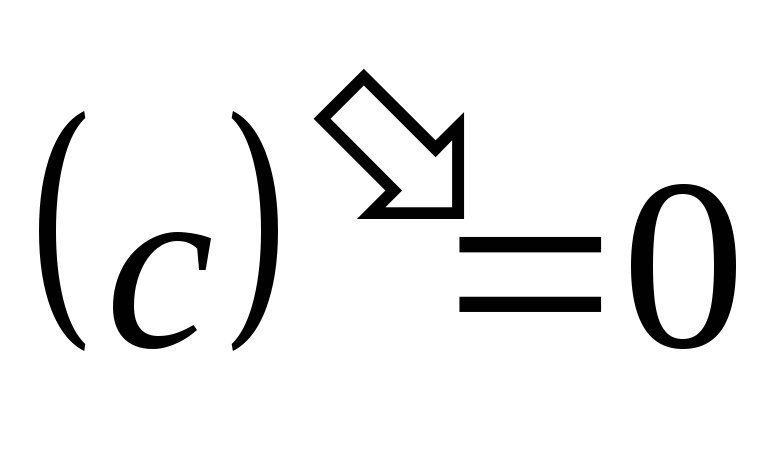
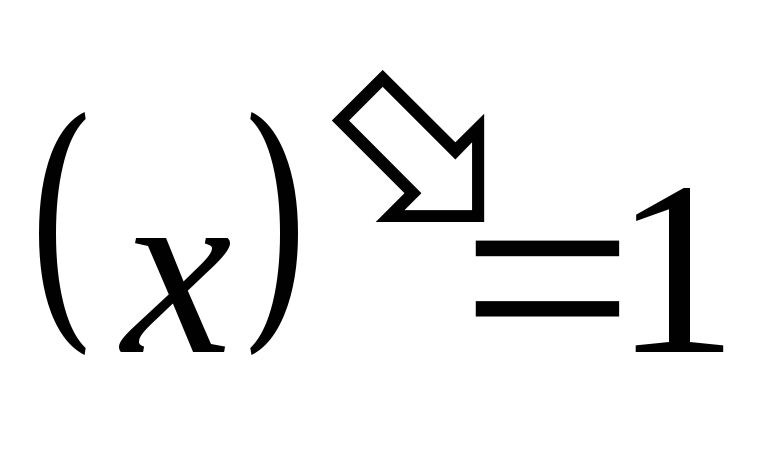
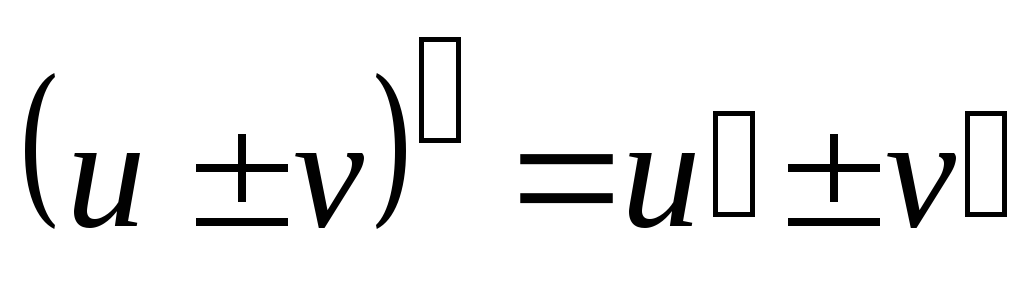
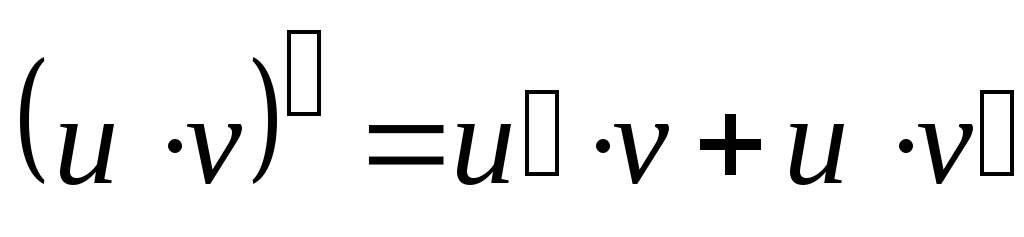

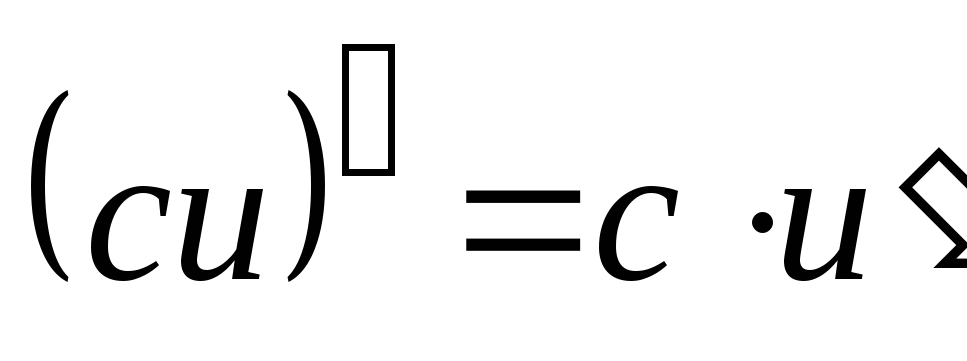
Если
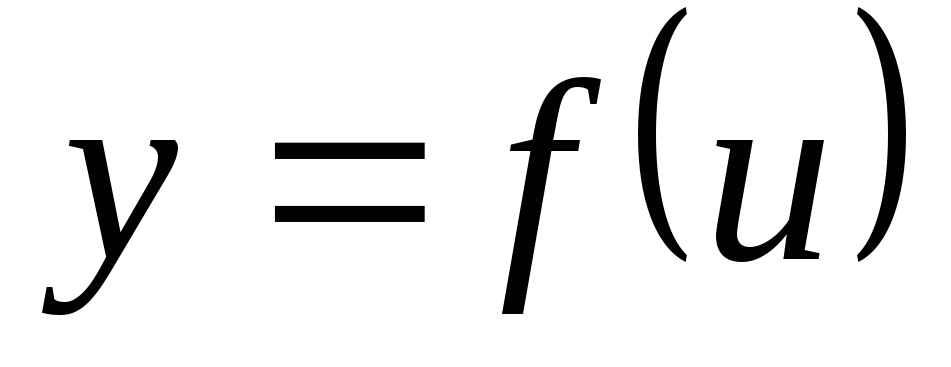 и
и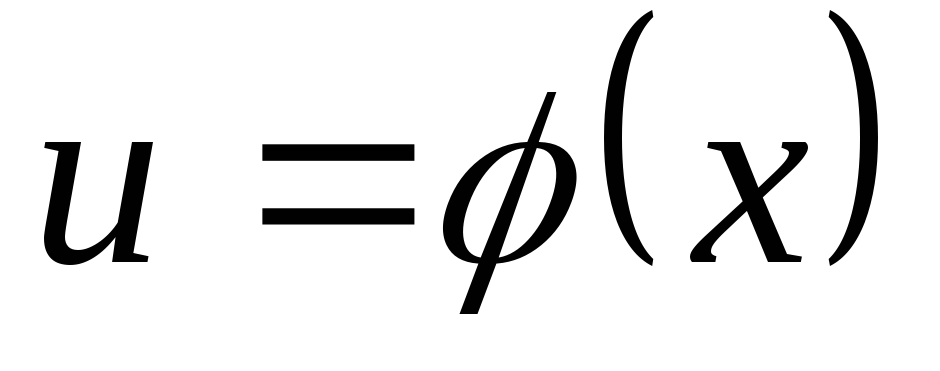 ,
т. е.
,
т. е.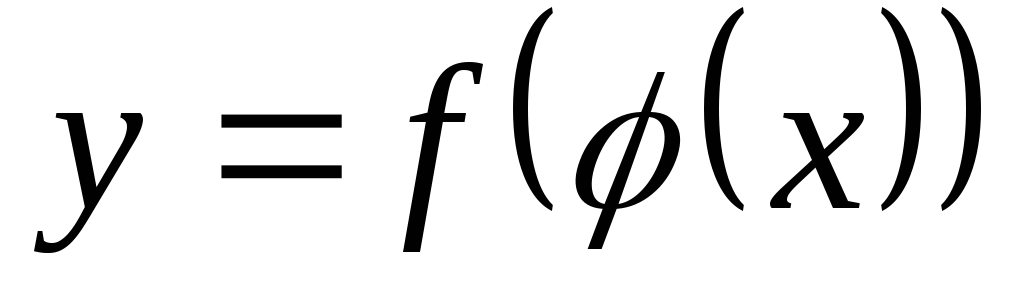 ,
то
,
то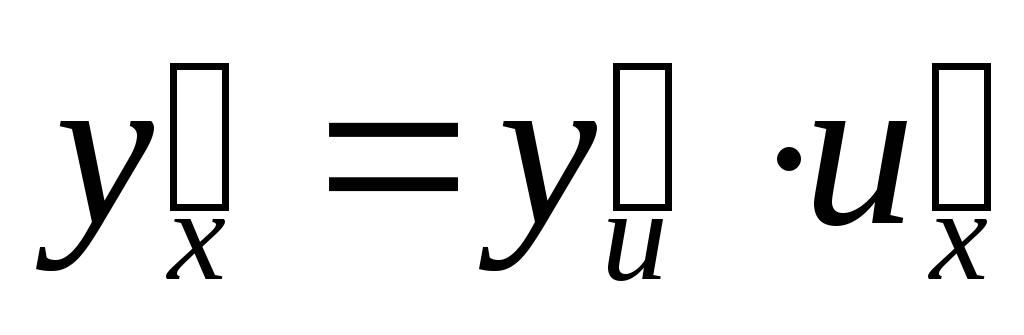 ,
гдеи и φ
– дифференцируемы.
,
гдеи и φ
– дифференцируемы.Если для функции
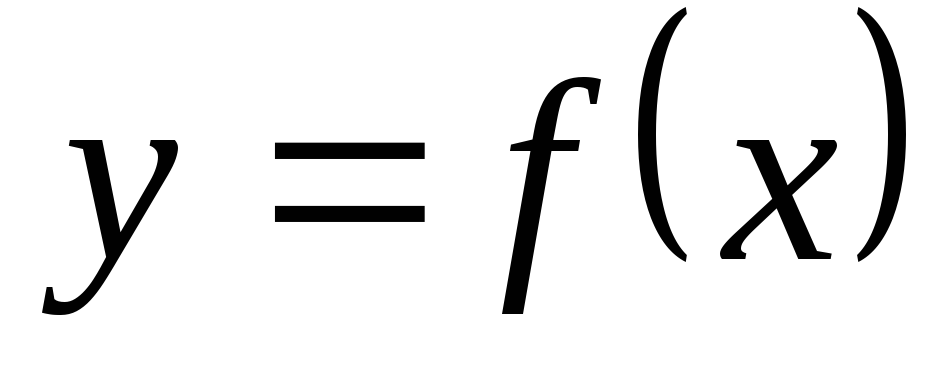 существует обратная дифференцируемая
функция
существует обратная дифференцируемая
функция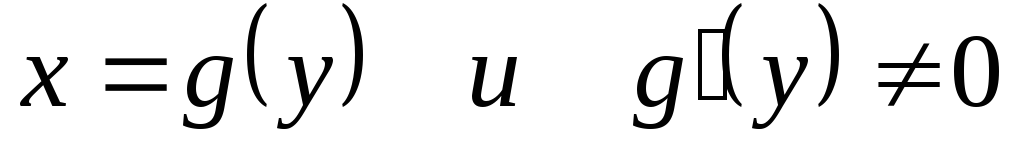 ,
то
,
то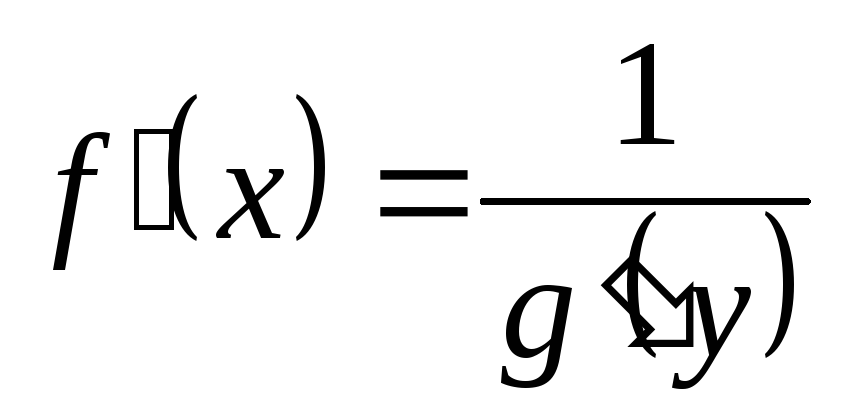 .
.
Задача.Найти производную функции
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Решение:
1)
![]()
![]() поэтому
по формуле (8) (см. таблицу производных)
поэтому
по формуле (8) (см. таблицу производных)
![]() .
.
2)
![]()
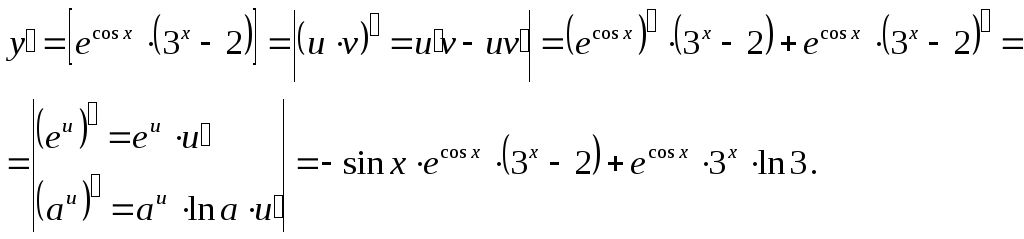
3)
![]()
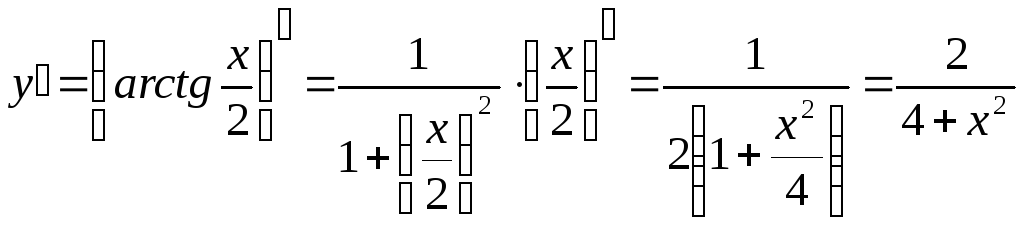 .
.
4)
![]()
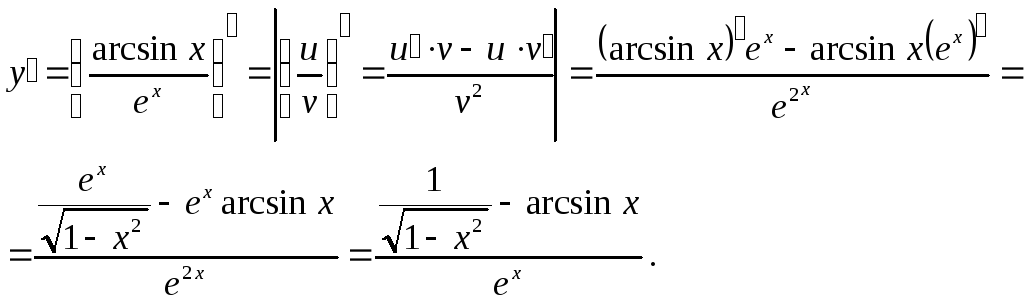
Определение:Производной второго порядка функции![]() называется производная от первой
производной, т. е.
называется производная от первой
производной, т. е.![]() .
Обозначают
.
Обозначают![]() .
.
Определение:Производнойn-го
порядка функции![]() называют производную от производной
(n– 1)-го порядка данной
функции. Обозначают
называют производную от производной
(n– 1)-го порядка данной
функции. Обозначают![]() .
.
