Раздел 2. Математический анализ

2.1. Методические указания и решение типового варианта контрольной работы № 3

Задача. Найти область сходимости степенного ряда:

.

Решение:Воспользуемся признаком Даламбера для нахождения области сходимости степенного ряда.

U_n=;U_n+1= ;

Интервал сходимости будет определяться неравенством , следовательно, 0х1.

Исследуем граничные точки.

При х = 0 получим числовой ряд, члены которого равны нулю, поэтому он сходится и х = 0 входит в область сходимости.

При х = 1 получим числовой ряд . Исследуем его на сходимость по предельному признаку сравнения, а для сравнения выберем гармонический ряд:

.

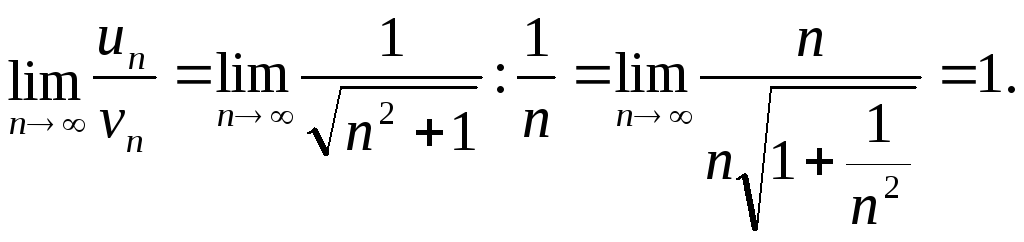
Так как предел отношения общих членов отличен от нуля, то оба ряда одновременно сходятся или расходятся, но так как гармонический ряд является расходящимся, то и исходный ряд расходится, следовательно, х = 1 не входит в область сходимости степенного ряда.

Ответ: .

Задача. Вычислить интеграл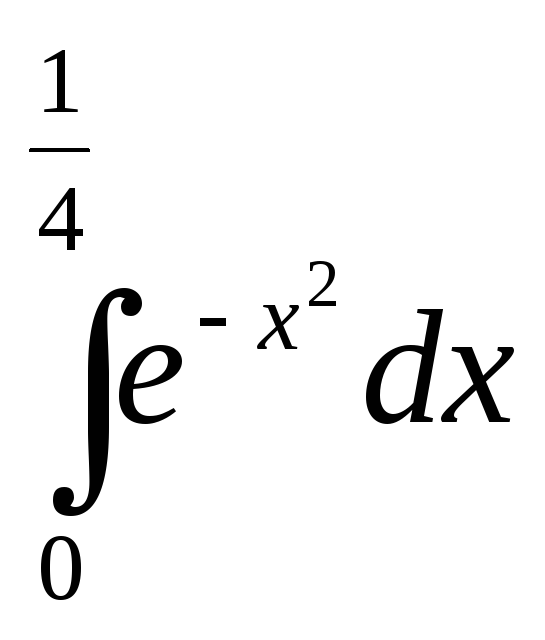с точностью до 0,001.

Решение.Используем разложение функциив степенной ряд по степеням х. Это возможно, так как ряд сходится к функции на промежутке (–¥; +¥), получим:

= 1 – +–+… .

Проинтегрируем обе части равенства на промежутке :

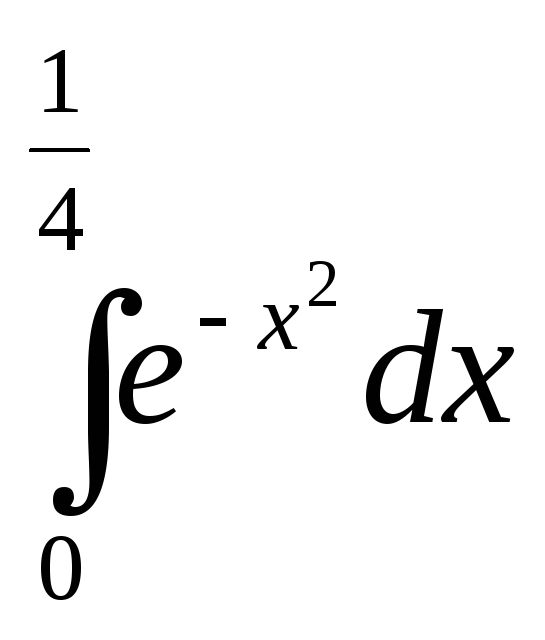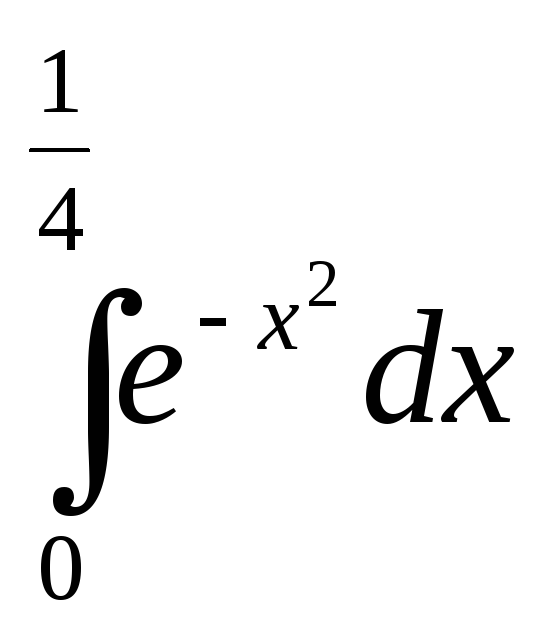=(1 –+–+…)dx;

= (x – +–+…);

= –+–+… .

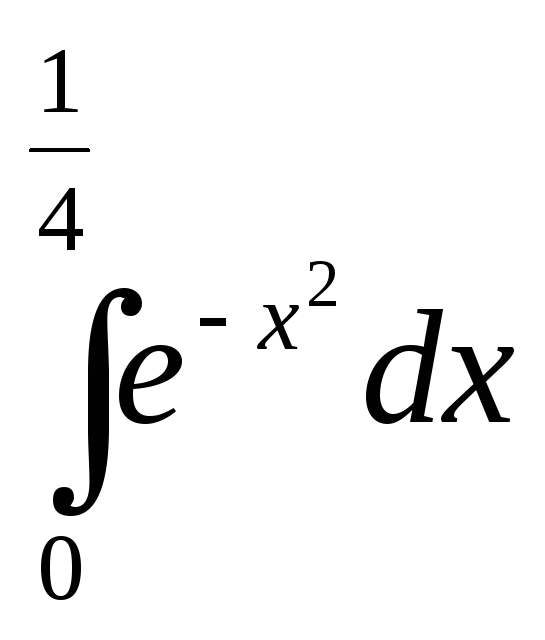Правая часть равенства представляет собой ряд лейбницевского типа.

Так как , что больше 0,001, а, что меньше 0,001, то для вычисления с заданной точностью достаточно взять два слагаемых, итак,

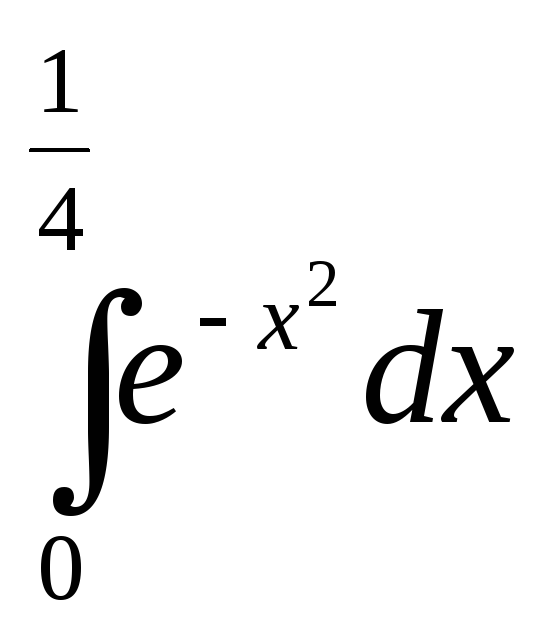
–= 0,245.

Ответ: 0,245.

Формула трапеций

, где ;шаг деления отрезканаnравных отрезков точками.

Остаточный член имеет вид .

Формула трапеций дает точное значение, если – линейная функция, так как.

Задача.Вычислить приближенно по формуле трапеций интегралприn= 10 и оценить погрешность вычислений.

Решение:Оценить остаточный член;

.

На отрезке при х = 0; в – а = 1,h= 0,1.

, следующие вычисления надо производить с четырьмя знаками после запятой.

Составим таблицу значений функции .

i	xi	xi2	yi
6	0,6	0,36	1,6977
7	0,7	0,49	0,6126
8	0,8	0,64	0,5273
9	0,9	0,81	0,4449
10	1,0	1	0,3679

i	xi	xi2	yi
0	0	0	1,0000
1	0,1	0,01	0,9900
2	0,2	0,04	0,9608
3	0,3	0,09	0,9139
4	0,4	0,16	0,8521
5	0,5	0,25	0,7788

.

, следовательно, .

После округления окончательно получаем .

Формула Симпсона (формула парабол) (n–четное)

, где .

Остаточный член имеет вид .

Задача.Вычислить интегралпо формуле Симпсона приn= 10 и оценить остаточный член.

Решение:Оценим остаточный член.

, ,,,

.

имеет наибольшее значение на при х = 1,m= 5,

.

Составим таблицу значений, запишем ординаты с четными и нечетными номерами в разные столбцы:

i	xi	xi2	yi, i=0, 10	y2m	y2m–1
0	0,0	0,00	1,000		1,0101
1	0,1	0,01
2	0,2	0,04		1,0407	1,0942
3	0,3	0,09
4	0,4	0,16		1,1735	1,2840
5	0,5	0,25
6	0,6	0,36		1,4333	1,6323
7	0,7	0,49
8	0,8	0,64		1,8965
9	0,9	0,81			2,2479
10	1,0	1,0	2,7188

Суммы: у₀ + у₁₀ = 3,7188,

åу_2m = 5,44,

åу_2m–1 = 7,2685.

По формуле Симпсона получаем: ; округляем до четырех знаков, окончательно получим.

Задача. Решить систему дифференциальных уравнений с помощью составления характеристического уравнения

.

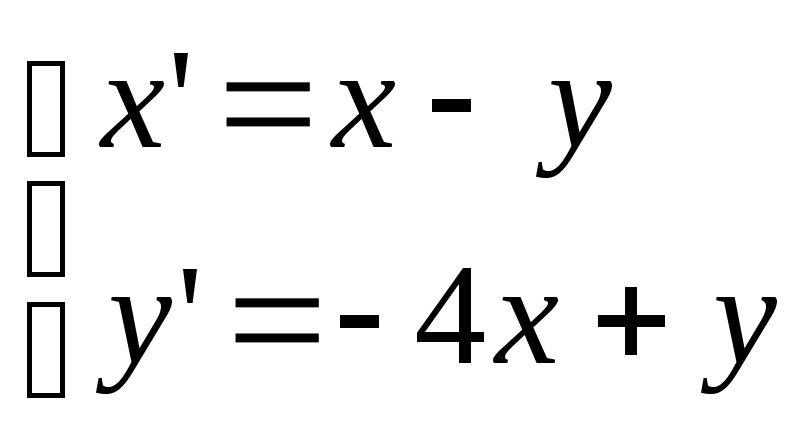Решение:Фундаментальную систему решений будем отыскивать в виде;, тогда,. Подставим полученные значения в систему уравнений:

.

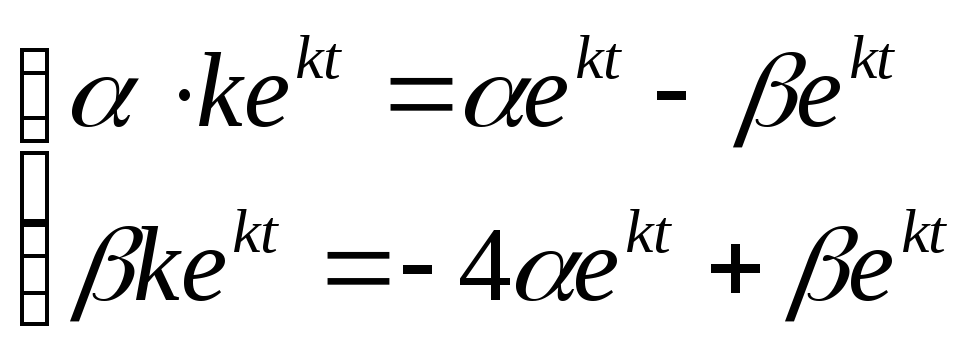
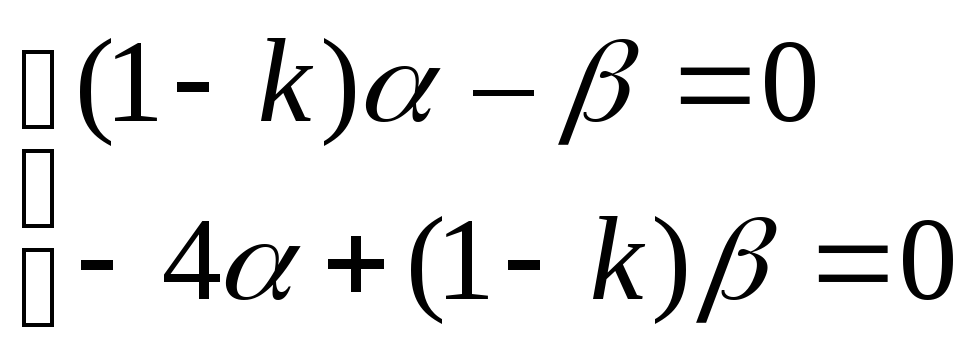Составим характеристическое уравнение 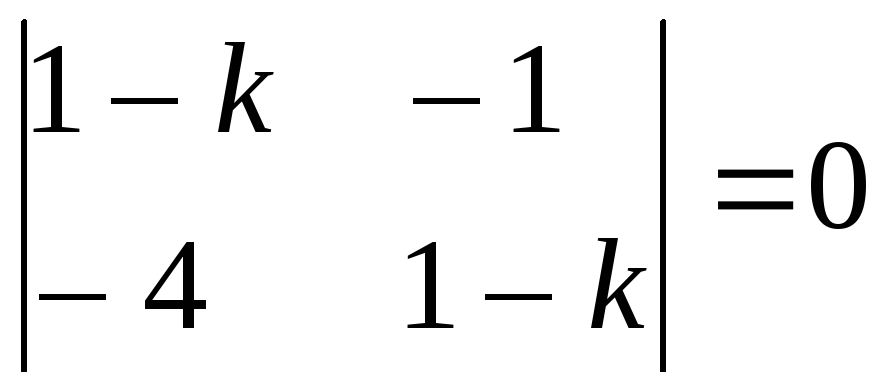или

(1 – к)²– 4 = 01 – к =±2, откуда 1 – к = –2, к = 3 или 1 – к = 2, к = –1.

При к = –1 получим систему уравнений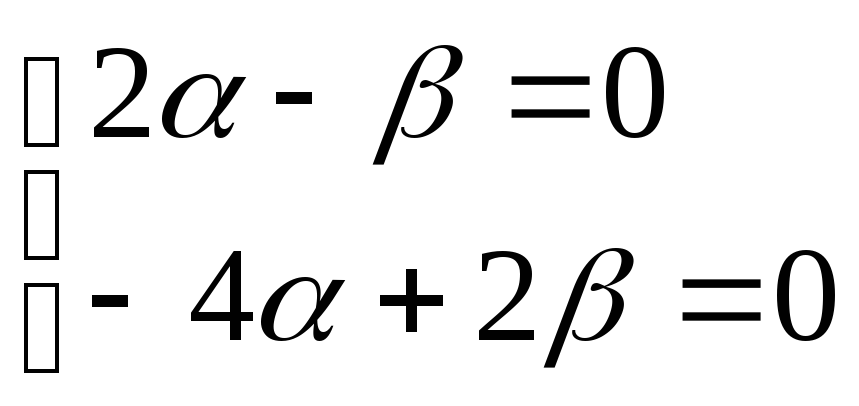. Пусть, тогда, откуда,– фундаментальная система решений.

При к = 3 получим систему уравнений: 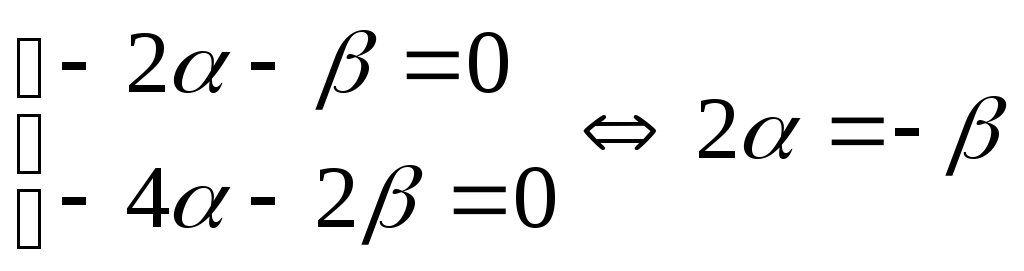. Пусть, тогда, откуда,.

Общее решение системы уравнений запишется в виде:

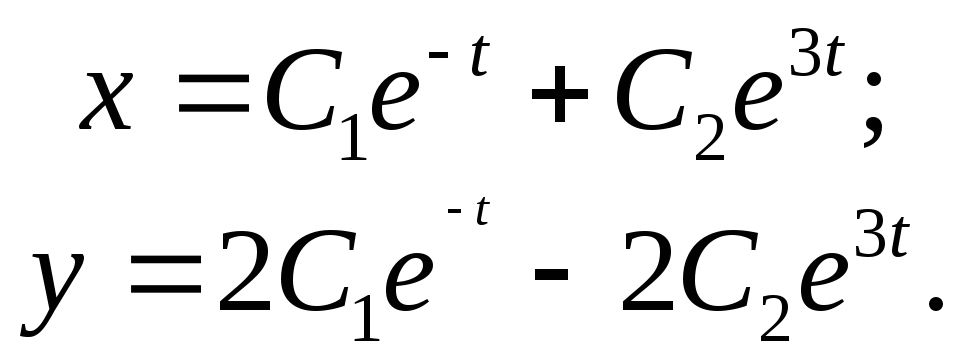
Задача.Разложить в степенной ряд по степенямxрешение дифференциального уравнения, записать первые три, отличных от нуля, члена разложения.

Решение:.

Продифференцируем исходное уравнение не менее двух раз.

,

,

.

Имеем: , , , , подставим полученные значения в степенной ряд: , получим приближенное решение дифференциального уравнения .

Задача.Записать уравнение кривой, проходящей через точку P (1,2), для которой площадь треугольника, образованного радиус-вектором любой точки кривой касательной в этой точке и осью абсцисс, равна 2.

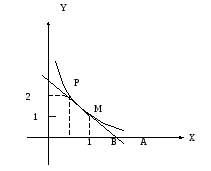
–произвольная точка кривой. ОМ – радиус-вектор. МА – касательная к кривой. Известно, что . Найти уравнение кривой.

Решение:

, так как , то. Изимеем:или, тогда. Площадь треугольника ОМА равна, и, так как по условию задачи, получим уравнение. Решим это уравнение, выполнив некоторые преобразования,,, последнее уравнение – линейное, первого порядка относительно, поэтому используем подстановку;;;;;;,;;;.

Итак, .

По условию задачи кривая проходит через точку Р (1, 2), поэтому С = 0, так как 1 = 2С + 1; следовательно, искомая кривая имеет видилиxy = 2 – гипербола.