
- •Сахалинский государственный университет
- •Никитина Алла Борисовна, Чан Сун Нами
- •Программа курса «Математика»
- •Раздел 6. Дифференциальное исчисление функций
- •Раздел 7. Элементы интегрального исчисления
- •Раздел 8. Элементы теории рядов
- •Раздел 9. Элементы теории дифференциальных уравнений
- •Раздел 10. Элементы теории поля
- •1.2. Методические указания и решение типового варианта
- •Предел функции в точке
- •Дифференциал функции в точке
- •Основные теоремы дифференциального исчисления
- •Методы исследования функций и поведения их графиков.
- •Функция двух переменных
- •1.3. Вопросы для контроля
- •Раздел 2. Математический анализ
- •2.1. Методические указания и решение типового варианта контрольной работы № 3
- •2.2. Методические указания и решение типового варианта контрольной работы № 4 Элементы теории поля
- •2.3. Вопросы для контроля
- •Раздел 3. Теория вероятностей
- •3.1. Методические указания и решение типового варианта
- •Контрольная работа № 1 по теме: «Элементы векторной алгебры и аналитической геометрии»
- •Контрольная работа № 2
- •Контрольная работа № 3
- •Контрольная работа № 4
- •Контрольная работа № 5
- •Значение функции Пуассона
- •Список литературы
Контрольная работа № 1 по теме: «Элементы векторной алгебры и аналитической геометрии»
Задание
№ 1.1. Найти: а)
![]() ,
,![]() ;
;
б)
модуль вектора
![]() ;
;
в)
скалярное произведение ![]() ;
;
г) векторное произведение векторов;
д)
смешанное произведение векторов
![]() ;
;![]() .
.
А В С
1.10 (3,1–2) (–1,6,1) (–1,1,6)
1.11 (3,1,4) (–1,0,1) (1,7,3)
1.12 (3,5,4) (5,8,3) (1,2,–2)
1.13 (2,4,3) (1,1,5) (4,9,3)
1.14 (9,5,5) (–3,7,1) (5,7,8)
1.15 (0,7,1) (2, –1,5) (1,6,3)
1.16 (1,1,2) (1, –1, –1) (3,5,1)
1.17 (6,6,1) (4,6,6) (4,2,0)
1.18 (7,5,3) (9,4,4) (4,5,7)
1.19 (6,8,2) (5,4,7) (2,4,7)
Задание
№ 1.2. Доказать, что
векторы
![]() образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора![]() в этом базисе.
в этом базисе.
|
|
|
|
|
|
|
1.20 |
(2,2,3) |
(1,3,2) |
(3,1,1) |
(7,1,6) |
|
1.21 |
(3,1,5) |
(–1,2,1) |
(1,4,2) |
(12,6,3) |
|
1.22 |
(2,1,4) |
(–1,1,1) |
(2,2,4) |
(3,–4,–3) |
|
1.23 |
(2,1,1) |
(–1,3,2) |
(3,–1,2) |
(–4,11,7) |
|
1.24 |
(3,3,2) |
(–2,4, –1) |
(4,–2,–1) |
(12,6,–9) |
|
1.25 |
(8,1,4) |
(3,1,1) |
(–6,–1,–3) |
(–4,2,–5) |
|
1.26 |
(4,1,8) |
(1,1,3) |
(–3,–1,–6) |
(9,–2,12) |
|
1.27 |
(2,7,4) |
(3,–5,0) |
(4,0,11) |
(33,24,39) |
|
1.28 |
(2,7,4) |
(3,–5,0) |
(4,1,1) |
(12,–33,–7) |
|
1.29 |
(1,0,3) |
(4,5,–2) |
(–1,4,5) |
(6,–20,–22) |
Задание
№ 1.3. Сила
![]() приложена к точке А. Вычислить:
приложена к точке А. Вычислить:
а)
работу силы
![]() ,
если точка ее приложения, двигаясь
прямолинейно, переместилась в точку В;
,
если точка ее приложения, двигаясь
прямолинейно, переместилась в точку В;
б)
модуль вращающего момента силы
![]() ,
точки В.
,
точки В.
|
|
|
|
|
|
1.30 |
(1,3,4) |
(2,0,–1) |
(–3,–1,–2) |
|
1.31 |
(1,0,3) |
(–2,0,3) |
(–2,–1,0) |
|
1.32 |
(3,2,1) |
(2,3,5) |
(–1,0,–3) |
|
1.33 |
(2,1,1) |
(–1,3,2) |
(3,–1,2) |
|
1.34 |
(–1,3,5) |
(–2,–5,9) |
(–1,–6,5) |
|
1.35 |
(–1,2,1) |
(2,–1,4) |
(4,–2,0) |
|
1.36 |
(1,–5,0) |
(–3,0,7) |
(–4,3,4) |
|
1.37 |
(2,3,1) |
(4,0,2) |
(5,–4,1) |
|
1.38 |
(0,–1,3) |
(2,4,6) |
(5,5,0) |
|
1.39 |
(3,1,–2) |
(0,1,4) |
(–3,2,5) |
Задание № 1.4. Заданы три точки пространства А, В и С (координаты точек взять из задания 1.1). Найти:
а) уравнение стороны АВ треугольника АВС;
б) периметр треугольника (до 0,01);
в) уравнение плоскости (АВС);
г) площадь треугольника (до 0,01).
Задание № 1.5. Проверить совместность системы линейных алгебраических уравнений и решить ее:
а) методом Крамера;
б) методом Гаусса;
в) матричным методом.
1.50 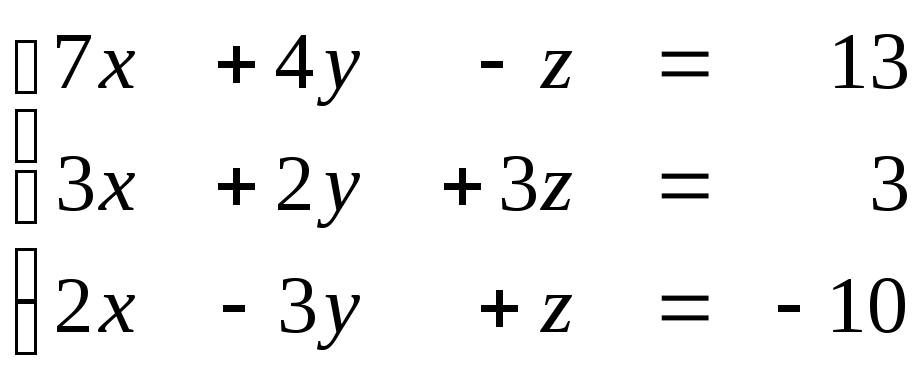 1.51
1.51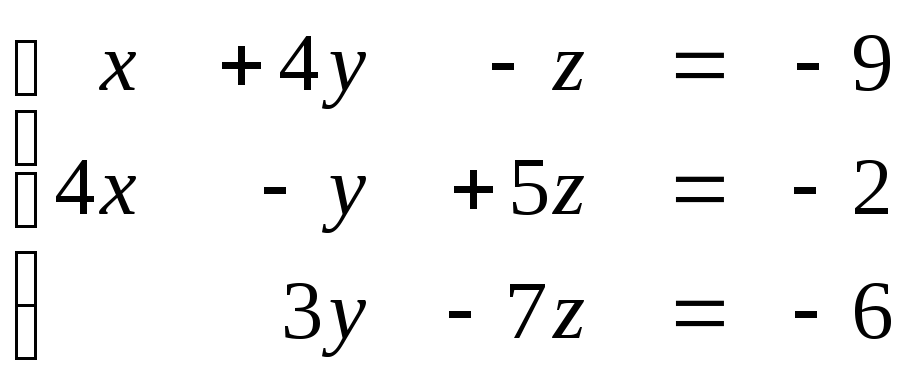
1.52 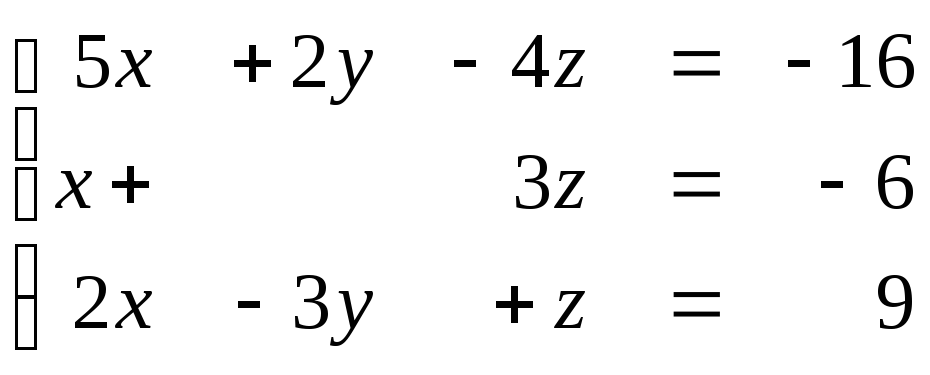 1.53
1.53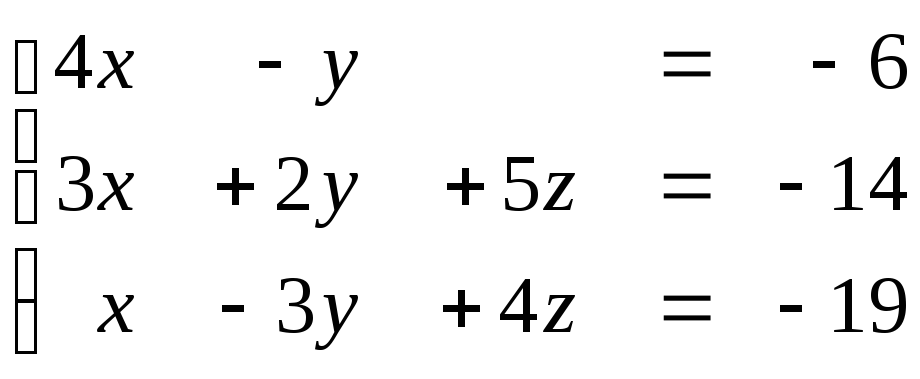
1.54 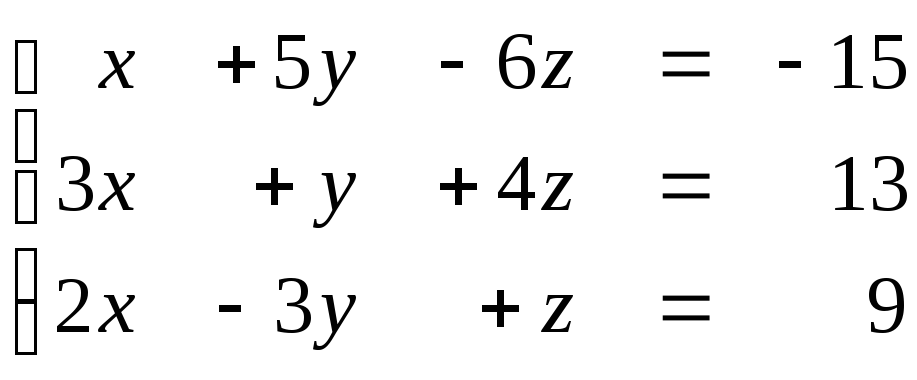 1.55
1.55
1.56 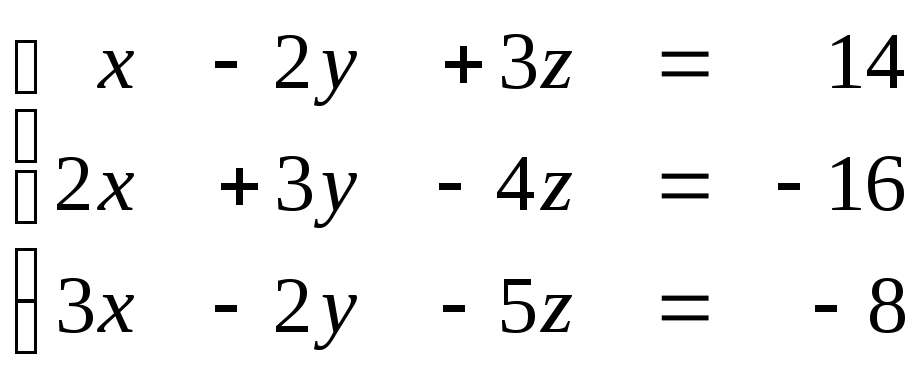 1.57
1.57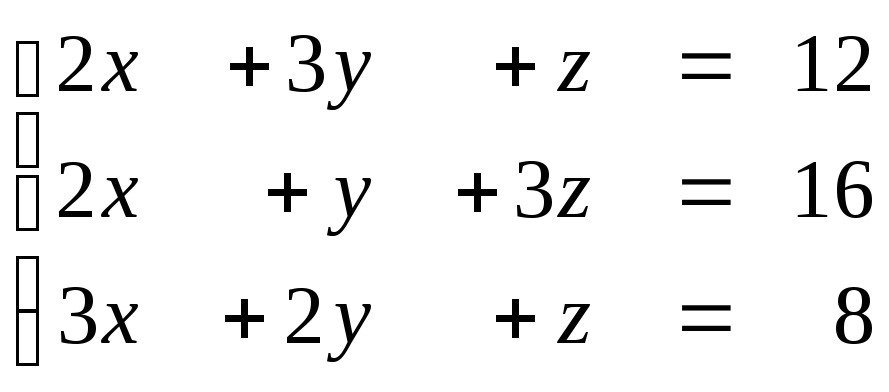
1.58 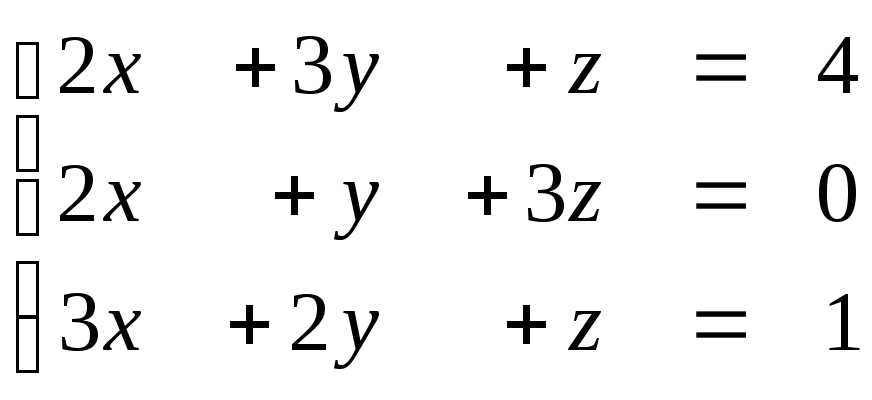 1.59
1.59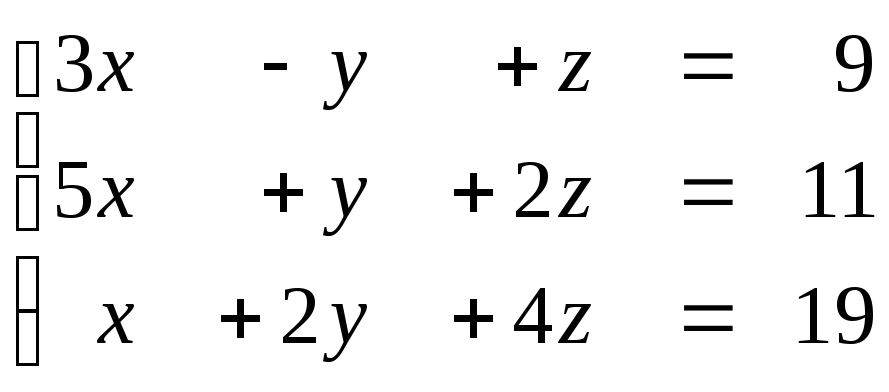
Приложение 2
Контрольная работа № 2
Задание № 2.1.Найти пределы функций:
|
№ |
а |
б |
в |
г |
|
1.1 |
|
|
|
|
|
1.2 |
|
|
|
|
|
1.3 |
|
|
|
|
|
1.4 |
|
|
|
|
|
1.5 |
|
|
|
|
|
1.6 |
|
|
|
|
|
1.7 |
|
|
|
|
|
1.8 |
|
|
|
|
|
1.9 |
|
|
|
|
|
1.10 |
|
|
|
|
Задание № 2.2.Исследовать функцию на непрерывность и построить график.
2.1
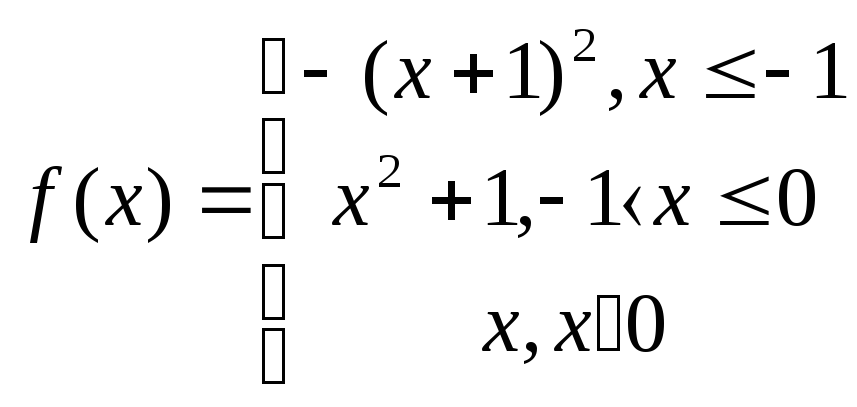 2.6
2.6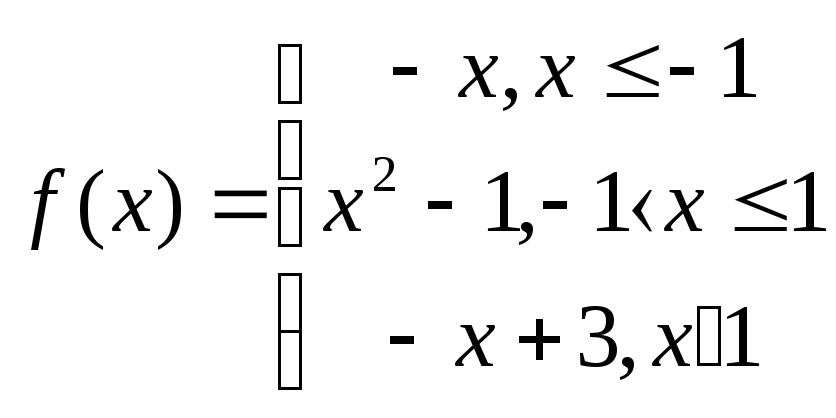
2.2
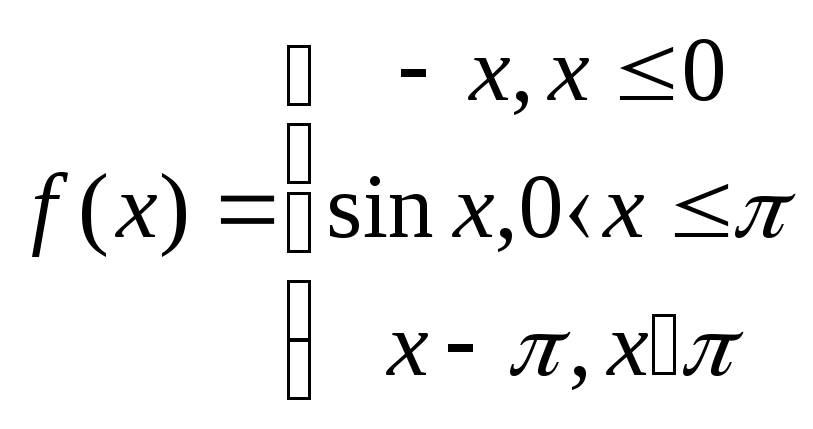 2.7
2.7
2.3
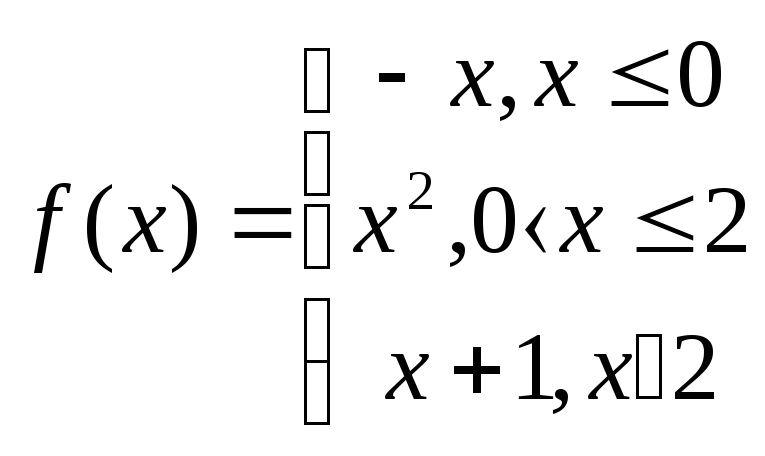 2.8
2.8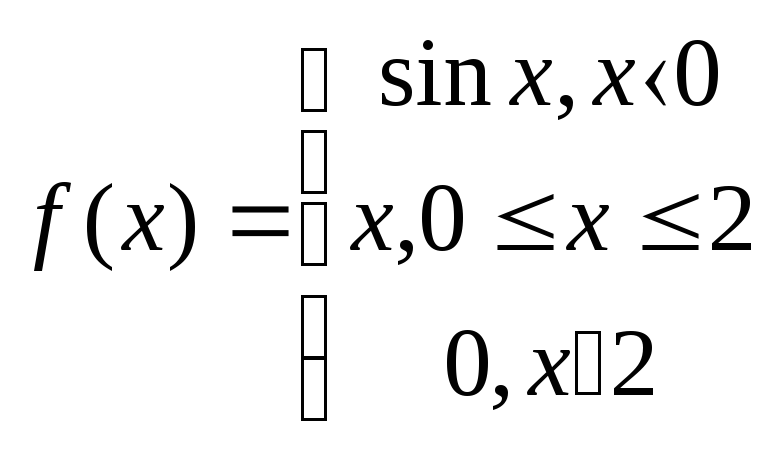
2.4
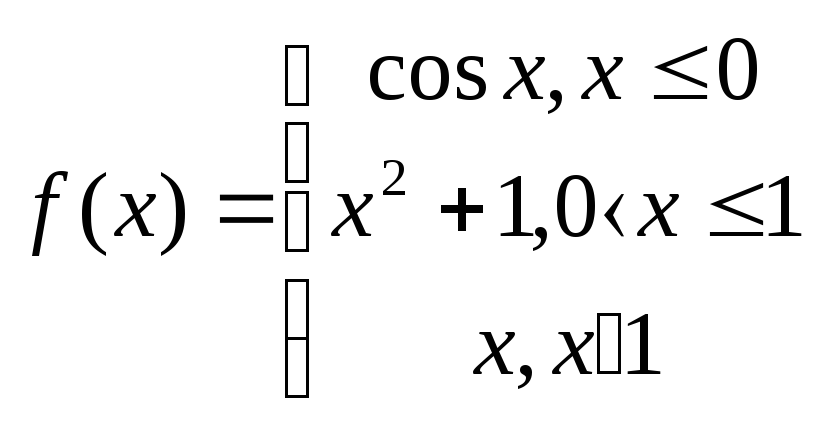 2.9
2.9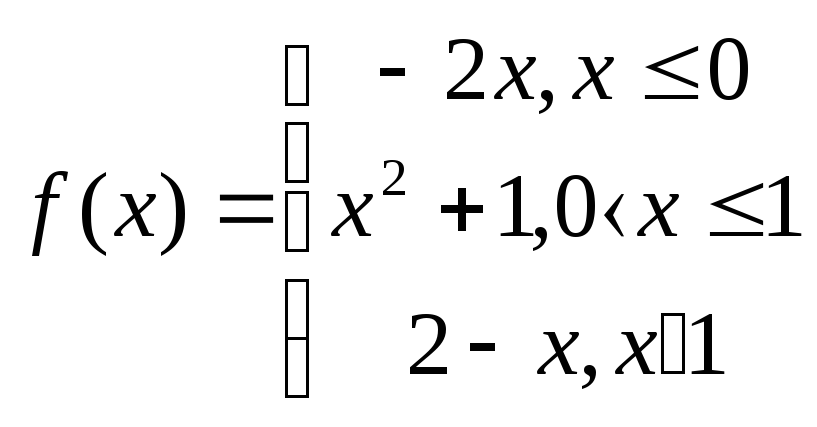
2.5
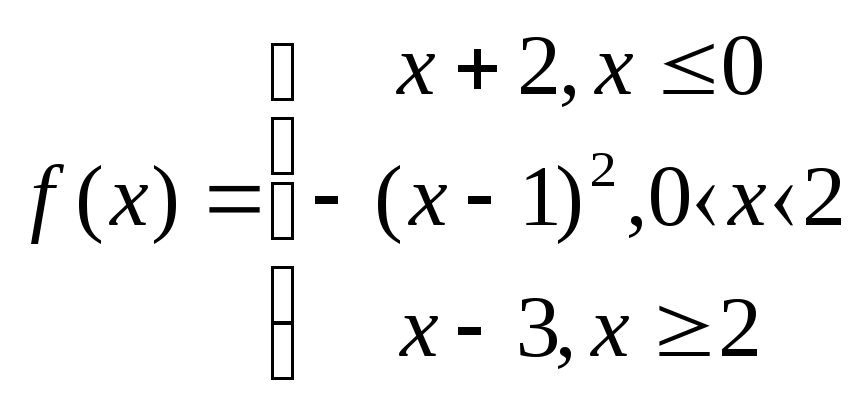 2.10
2.10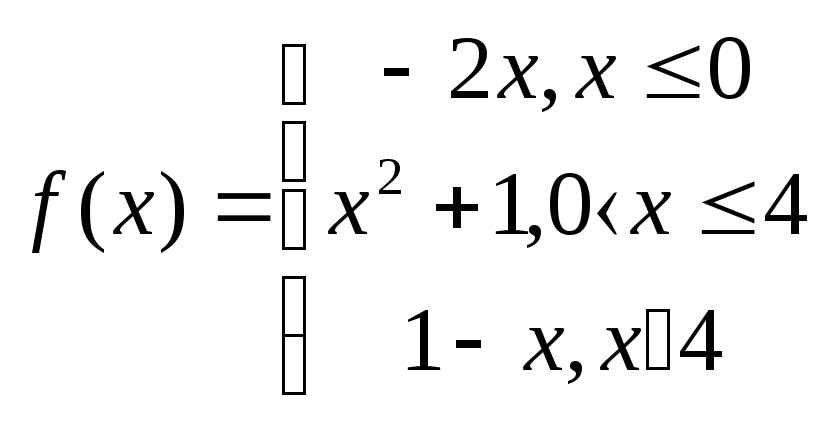
Задание № 2.3.Найти производные функций:
3.1 а)
![]() в)
в)![]()
б)
![]() г)
г)![]()
3.2 а)
![]() в)
в)![]()
б)
![]() г)
г)![]()
3.3 а)
![]() в)
в)![]()
б)
![]() г)
г)![]()
3.4 а)
![]() в)
в)![]()
б)
![]() г)
г)![]()
3.5 а)
![]() в)
в)![]()
б)
![]() г)
г)![]()
3.6 а)
![]() в)
в)![]()
б)
![]() г)
г)![]()
3.7 а)
![]() в)
в)![]()
б)
![]() г)
г)![]()
3.8 а)
![]() в)
в)![]()
б)
![]() г)
г)![]()
3.9 а)
![]() в)
в)![]()
б)
![]() г)
г)![]()
3.10 а)
![]() в)
в)![]()
б)
![]() г)
г)![]()
Задание № 2.4.Исследовать функцию и построить график.
4.1
![]() ; 4.6
; 4.6![]() ;
;
4.2![]() ; 4.7
; 4.7![]() ;
;
4.3
![]() ; 4.8
; 4.8![]() ;
;
4.4
![]() ; 4.9
; 4.9![]() ;
;
4.5
![]() ; 4.10
; 4.10![]() .
.
Задание № 2.5.Найти экстремум функции двух переменных.
5.1
![]() ;
;
5.2
![]() ;
;
5.3
![]() ;
;
5.4
![]() ;
;
5.5
![]() ;
;
5.6
![]() ;
;
5.7
![]() ;
;
5.8
![]() ;
;
5.9
![]() ;
;
5.10
![]() .
.
Задание № 2.6. Вычислить приближенно значение выражения с точностью до 0,001.
6.1![]() ; 6.6
; 6.6![]() ;
;
6.2![]() ; 6.7
; 6.7![]() ;
;
6.3![]() ; 6.8
; 6.8![]() ;
;
6.4![]() ; 6.9
; 6.9![]() ;
;
6.5![]() ; 6.10
; 6.10![]() .
.
Приложение 3
