33.Дифференцирование неявных функций.

Ответ - Если независимая переменная и функциясвязаны уравнением вида, которое не разрешено относительно, то функцияназывается неявной функцией переменной.

Пример

Всякую явно заданную функцию можно записать в неявном виде. Обратно сделать не всегда возможно.

Несмотря на то, что уравнение не разрешимо относительно, оказывается возможным найти производную отпо. В этом случае необходимопродифференцировать обе части заданного уравнения, рассматривая функцию как функцию от, а затем из полученного уравнения найти производную.

34. Дифференцирование параметрический заданных функций.

Ответ - Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.

Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем

Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х.

<< Пример 21.2

Пусть  

Найти у'х.

Решение: Имеем   x't=3t2,   y't=2t.   Следовательно,   у'х=2t/t2,   т. е. 

В этом можно убедиться, найдя непосредственно зависимость у от х.

Действительно, ТогдаОтсюдат. е.

35.Логарифмическое дифференцирование.

Ответ - Суть метода логарифмического дифференцирования

Суть такого дифференцирования заключается в следующем: вначале находится логарифмзаданной функции, а уже затем вычисляется от него производная. Пусть задана некоторая функция. Прологарифмируем левую и правую части данного выражения:

Далее продифференцируем полученное равенство при условии, что является функцией от, то есть найдемпроизводную сложной функции:

А тогда, выражая искомую производную , в результате имеем:

Производная показательно-степенной функции

Рационально использовать логарифмическое дифференцирование и при нахождении производной показательно-степенной (или степенно-показательной) функцииили "функции в степени функция", то есть в случае, когда заданная функция имеет вид. Логарифмируем левую и правую часть:

далее по свойствам логарифма

Тогда

Производную в левой части равенства находим как производную сложной функции, а в правой - как производную произведения:

36.Производные высших порядков; производные высших порядков от параметрически заданных функции.

Ответ - Если функция  имеет производную в каждой точке  своей области определения, то ее производная  есть функция от . Функция , в свою очередь, может иметь производную, которую называют производной второго порядка функции  (или второй производной) и обозначают символом . Таким образом

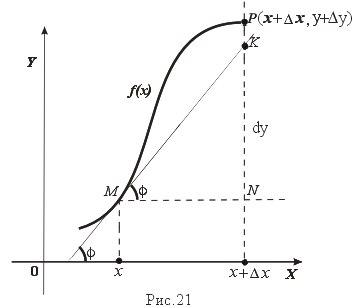
37.Понятие дифференциала функции. Геометрический смысл.

Ответ - Понятие дифференциала. Геометрический смысл. Если ф-ция y=f(x) имеет производную f`(x) в точке х, то произведение производной f`(x) на приращении Δх аргумента называется ДИФФЕРЕНЦИАЛОМ. Геометрический смысл: Дифференциал ф-ции f(х), соответствующий данным значениям х и Δх, равен приращению ординаты касательной к кривой y=f(x) в данной точке х. Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при D x->0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика.