16.Связь между функцией, пределом и бесконечно малой величиной.

Ответ - Теорема 1. Если функция имеет при() предел, равный, то ее можно представить в виде суммы этого числаи бесконечно малойпри(), т.е.. Теорема 2. Если функциюможно представить как сумму числаи бесконечно малойпри(), то числоесть предел этой функции при(), т.е..

17.Основные теоремы о пределах.

Ответ - Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.

Þ .

Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).

Þ .

Теорема 3. Предел постоянной равен самой постоянной.

.

Доказательство. f(x)=с,    докажем, что    .

Возьмем  произвольное e>0. В качестве d можно взять любое

положительное число. Тогда при 

.

Теорема 4. Функцияне может иметь двух различных пределов в

одной точке.

Доказательство. Предположим противное. Пусть

и  .

По теореме о связи предела и бесконечно малой функции:

f(x)-A=- б.м. при,

f(x)-B=- б.м. при.

Вычитая эти равенства, получим:

 B-A=-.

Переходя к пределам в обеих частях равенства при , имеем:

B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.

Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при , то и алгебраическая сумма имеет предел при, причем предел алгебраической суммы равен алгебраической сумме пределов.

.

Доказательство. Пусть ,,.

Тогда, по теореме о связи предела и б.м. функции:

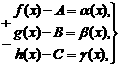где - б.м. при.

Сложим алгебраически эти  равенства:

f(x)+g(x)-h(x)-(А+В-С)=,

где б.м. при.

По теореме о связи предела и б.м. функции:

А+В-С=.

Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при , то и произведение имеет предел при, причем предел произведения равен произведению пределов.

.

Следствие. Постоянный множитель можно выносить за знак предела.

.

Теорема 7. Если функции f(x) и g(x) имеют предел при ,

причем , то и их частное имеет предел при, причем предел частного равен частному пределов.

,  .

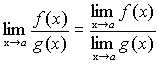18.Признаки существования пределов: теорема о пределе промежуточной функции(доказательство);теорема о пределе монотонной функции(б/д).

Ответ - (О пределе промежуточной функции).

Если имеет место соотношение и,, то и

Пример

Задание. Найти предел функциив точке, если известно, что имеет место соотношение:и,

Решение. Найдем пределы заданных функций ипри:

А тогда по теореме о предел промежуточной функции и

Ответ. 

Предел монотонной функции

Теорема

(О пределе монотонной функции).

Если функция является монотонной и ограниченной в областиили, то соответственно существует еелевый пределили ееправый предел.

19.Первый замечательный предел.

Ответ -  Первый замечательный предел    

Рассматривая отношение ипри стремлении аргументак нулю, имеем отношение двух бесконечно малых величин. А это есть неопределенность вида.

Доказательство 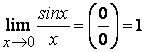строится на геометрическом представлении функцийв окружности единичного радиуса и  теоремы о том, что центральный угол измеряется дугой, на которую он опирается. Сравнивая, приходим к двойному неравенству.  Дальнейшие очевидные преобразования и переход к пределу при стремлении аргументак нулю, а также использование теоремы о пределах трех монотонных функций[1]приводят к доказательству того, что. Отсюда следует, что.

Основным достоинством этого предела, почему он и называется замечательным, является эквивалентность двух бесконечно малых величин и его аргумента:.  Отсюда получаем и другие эквивалентные функции при, а именно,

Пусть т. е.бесконечно малая приМожно получить еще несколько пар эквивалентных функций, которые для студентов технических специальностей значительно упрощают вычисления.