2.3. Скорость точки

Скорость – векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.

Скорость точки всегда направлена по касательной к траектории ее движения.

П

Рис. 2.6

усть заданы уравнения движения точки в пространстве:X=f₁(t); Y = f₂(t); Z = f₃(t) (рис. 2.6).

Р

Рис. 2.6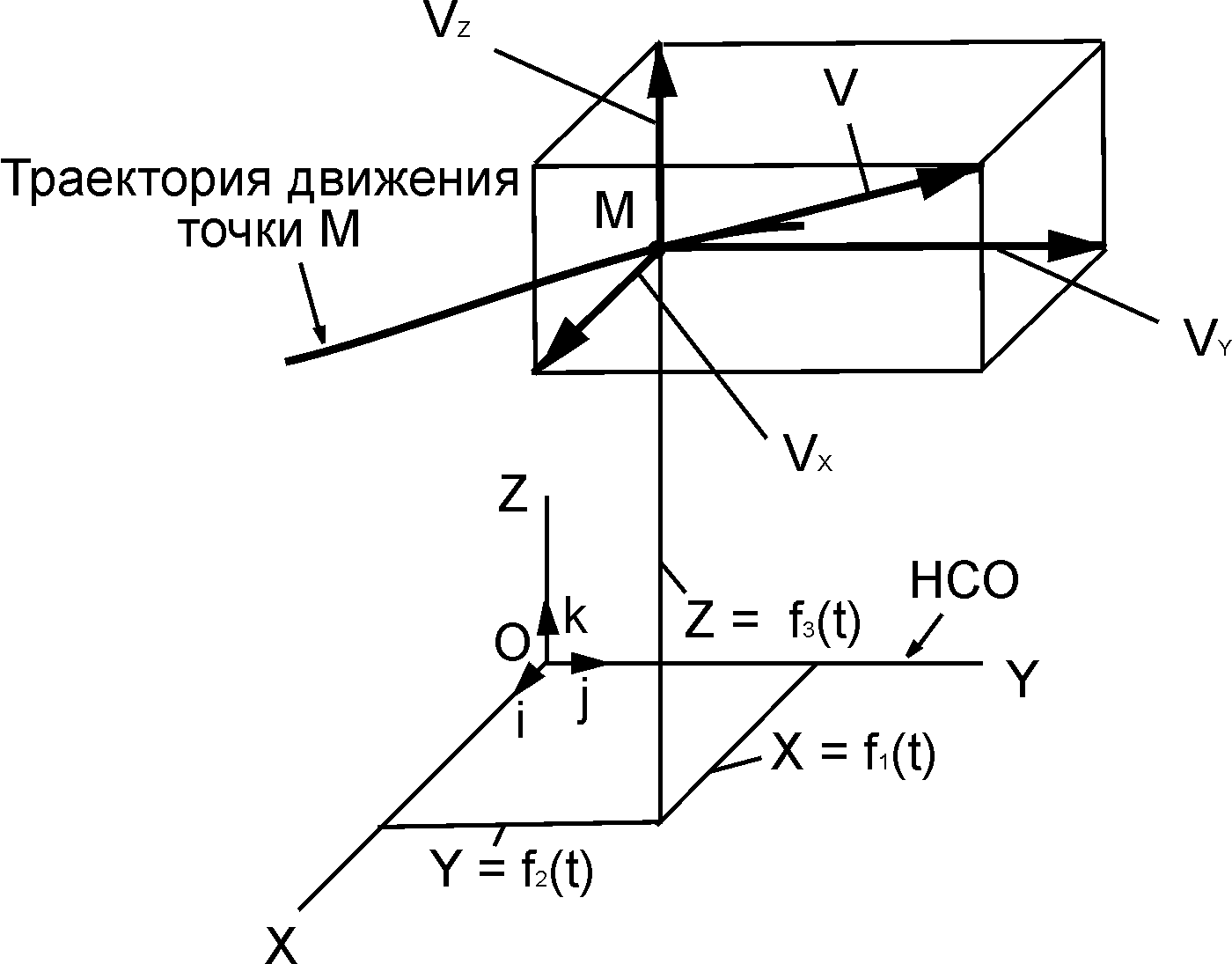

азложим векторV скорости точки на составляющие по координатным осям: V = V_X + V_Y + V_Z. Векторы V_X, V_Y, V_Z называют компонентами скорости по координатным осям. Вектор V скорости можно выразить векторным равенством:

V=i·V_X+j·V_Y+k·V_Z,

где V_X, V_Y, V_Z – проекции скорости V на соответствующие координатные оси.

Сравнивая последние формулы, запишем равенство

V = V_X + V_Y + V_Z = i·V_X+j·V_Y+k·V_Z.

Из этого равенства имеем:

V_X= i·V_X; V_Y= j·V_Y; V_Z= k·V_Z.

Проекции скорости на координатные оси системы отсчета равны первым производным по времени от соответствующих уравнений движения:

V_X = dX/dt =; V_Y = dY/dt = ; V_Z = dZ/dt = ,

где точка (·) означает символ однократного дифференцирования функции по времени.

Зная проекции скорости на координатные оси, находят модуль скорости по формуле

.

Ориентацию вектора скорости V в системе отсчета XOYZ определяют по направляющим косинусам:

cos(V, i) = V_X/V; cos(V, j) = V_Y/V; cos(V, k) = V_Z/V.

Движение точки в плоскости XOY (рис. 2.7) задается двумя уравнениями движения: X = f₁(t); Y = f₂(t). Модуль и направление скорости точки в этом случае определяются по формулам:

;

cos(V, i) = V_X/V; cos(V, j) = V_Y/V.

П

Рис. 2.7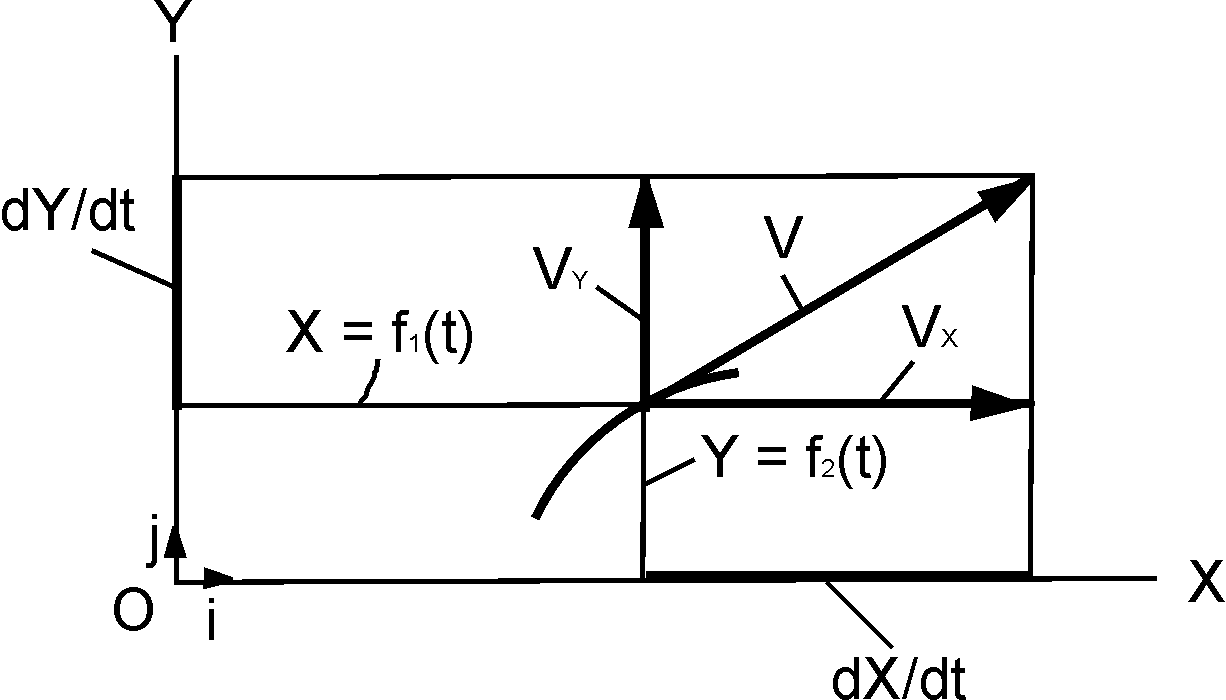

рямолинейное движение точки (рис. 2.8) задается одним уравнениемX = f(t).

В

Рис. 2.8

этом случае модуль скорости точки равен абсолютной величине проекции скорости на координатную ось ОХ.

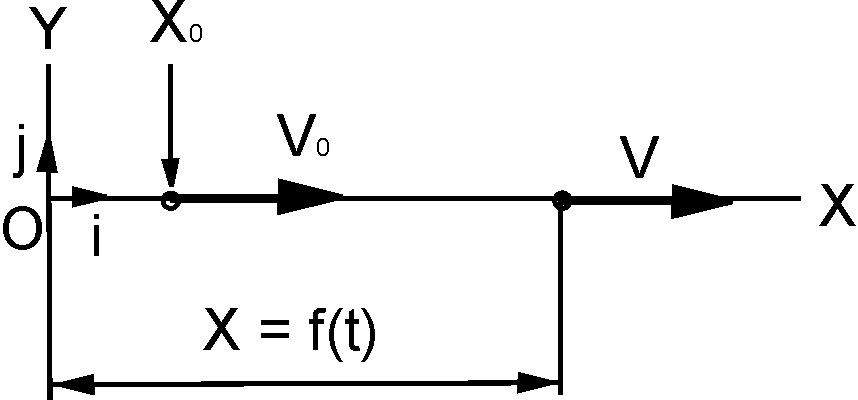
V = |V_X| = |dX/dt|.

При V_X > 0 точка движется в сторону увеличения координаты Х, при V_X < 0 – противоположно направлению оси.

2.4. Ускорение точки

Ускорение – векторная величина, характеризующая быстроту изменения величины и направления скорости.

Ускорение всегда направлено в сторону вогнутости траектории движения.

Рассматривается движение точки на плоскости в системе отсчета XOY (рис. 2.9) по заданным уравнениям движения X = f₁(t); Y = f₂(t). Согласно рис. 2.9 запишем векторное равенство

а = а_x+a_y = i·a_x+j·a_y,

где а – ускорение точки; а_x, a_y – компоненты ускорения по координатным осям; a_x, a_y – проекции ускорения на координатные оси.

Р

Рис. 2.9

аспространяя полученный результат на пространство (система отсчетаOXYZ), получим

а = а_x+ a_y+ a_z = i·a_x+j·a_y+k·a_z .

Р

Рис. 2.10

ассматривается движение точки по прямой линии согласно заданному уравнению движениюX = f(t) (рис. 2.10).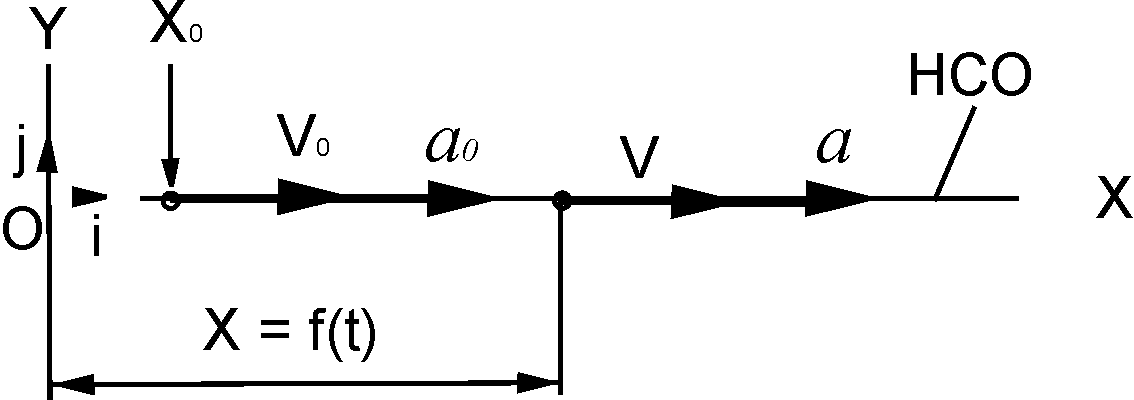

При таком движении справедливо равенство а = а_x = i·a_x. На рис. 2.10 дополнительно показано ускорение а₀ – начальное ускорение точки при t₀ = 0.

Проекции ускорения а на координатные оси в технической литературе обозначаются так, как это показано на рис. 2.9.

Проекции ускорения точки на координатные оси равны вторым производным по времени от соответствующих уравнений движения или первым производным по времени от проекций скорости на соответствующие оси.

a_x = d₂X/dt² = =dV_x/dt;

a_y = d₂Y/dt² = =dV_y/dt;

a_z = d₂Z/dt² = = dV_z/dt.

Обозначение (··) – это символ двойного дифференцирования по времени.

Модуль ускорения находится по следующим формулам:

a = (точка движется в пространстве);

a = (точка движется в плоскости);

a = || (точка движется по прямой линии).

Направляющие косинусы находятся по следующим формулам:

cos(a,i) = a_x/ a; cos(a,j) = a_y/ a; cos(a,k) = a_z/ a.

Зная направляющие косинусы, вектор ускорения а ориентируют в пространстве.

Примечания:

1. Если проекции ускорения на координатные оси положительны (> 0, > 0, > 0), то компоненты ускорения по координатным осям (а_x, a_y, a_z) направлены в те же стороны, что и единичные векторы (I, j, k) системы отсчета OXYZ.

2. Если проекции ускорения на координатные оси отрицательны (< 0, < 0, < 0), то компоненты ускорения по координатным осям (а_x, a_y, a_z) направлены в стороны, противоположные ортам (I, j, k) системы отсчета OXYZ.

Рассмотрим более подробно прямолинейное движение точки по координатной оси ОХ (рис. 2.10) по заданному уравнению движения X = f(t).

Если проекция скорости и проекция ускорения точки совпадают по знаку, то точка движется ускоренно. При >0 и>0 точка движется в сторону увеличения координаты Х ускоренно. Если<0 и<0, то точка движется в сторону уменьшения координаты Х ускоренно. Если>0 и<0, то точка движется в сторону увеличения координаты замедленно. Если<0 и>0, то точка движется в сторону уменьшения координаты Х замедленно.

Если проекция ускорения на ось ОХ постоянна (=const), то такое движение называют равнопеременным. При условии, что =const ≠ 0, уравнение равнопеременного движения точки записывают в виде

X = X₀ + ₀·t + (·t²)/2,

где X₀ – значение координаты точки в начальный момент времени; ₀ - проекция начальной скорости V₀ на координатную ось ОХ в начальный момент времени.

Если =const > 0, то такое движение называют равноускоренным.

Если =const < 0, то движение точки называют равнозамедленным.

Если = 0, то такое движение называютравномерным. Уравнение равномерного движения имеет вид X = X₀+·t.

При условии, что = f(t) ≠ const, для получения уравнения движения выражение = f(t) необходимо дважды проинтегрировать.

Пусть, например, = 2t. Представим это выражение в виде d/dt=2t. Разделим переменные в этом дифференциальном уравнении d=2tdt. Первый интеграл от этого выражения имеет вид =2(t²/2)+C₁ = t² +C₁, где С₁ – постоянная интегрирования, которую находят по начальным условиям движения. Пусть при t₀ = 0 проекция начальной скорости V₀ на ось ОХ не равна нулю: ₀≠ 0. Тогда при t₀ имеем ₀ =(t₀)²+C₁. Откуда С₁ = ₀. Внося значение постоянной С₁ в выражение, полученное при первом интегрировании, имеем =t² + ₀. Так как =dX/dt, то после разделения переменных имеем следующее дифференциальное уравнение движения dX= t²dt+₀dt. Интегрируя это уравнение, получим X = t³/3 +₀t+C₂, где С₂ – постоянная интегрирования, определяемая по начальным условиям движения. Пусть при t₀ = 0 координата Х₀ ≠ 0. Тогда X₀=(t₀)³/3+₀t₀+C₂ или С₂ = Х₀. Окончательно имеем уравнение прямолинейного движения

X=(t)³/3+₀t+X_o.

Таким образом, если заданы уравнения движения точки в координатной форме, то можно в любой момент времени определить следующие кинематические характеристики:

1. траекторию движения;

2. положение точки на траектории движения;

3. проекции скорости на координатные оси, а следовательно, и модуль скорости;

4. ориентацию вектора скорости в системе отсчета по направляющим косинусам;

5. проекции ускорения на координатные оси и модуль ускорения;

6. положение вектора ускорения в системе отсчета по направляющим косинусам.