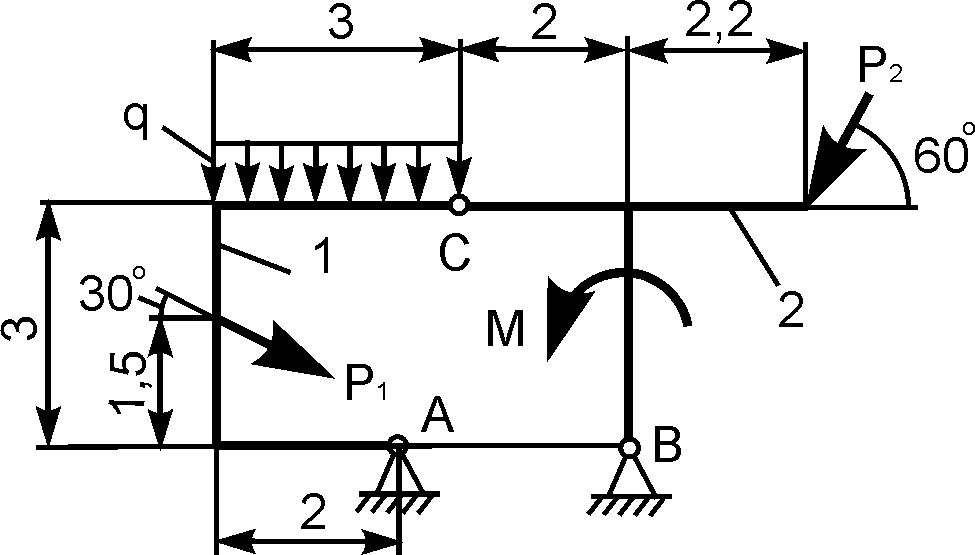
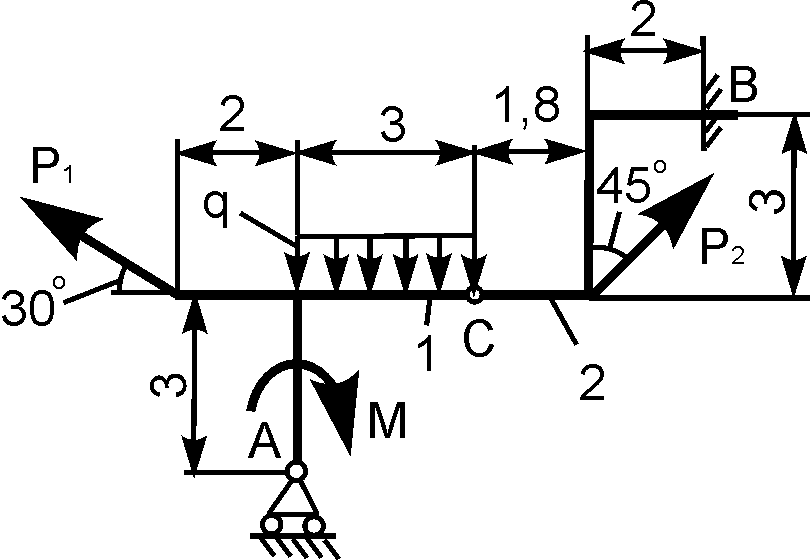
1.22. Определение реакций опор составных конструкций
Статически определимые задачи – задачи, в которых реакции внешних связей находятся из уравнений равновесия.
В
Рис. 1.60
Дано: Р, М, q. Определить реакции внешних связей в точках А и В.
Порядок решения таких задач рассмотрен ранее, поэтому сразу же записывают уравнения равновесия для плоской произвольной системы сил:
∑ Fix = 0 = XА – RBsinα = 0; (1)
∑ FiY = 0 = YA – Q – P + RBcosα = 0; (2)
∑ MiA = 0 = – Q·1 – P·4 – M + RBsinα·3,5tgα + RBcosα·7,5 = 0. (3)
Очевидно, что из трех уравнений равновесия легко находятся реакции внешних связей XA, YA, RB.
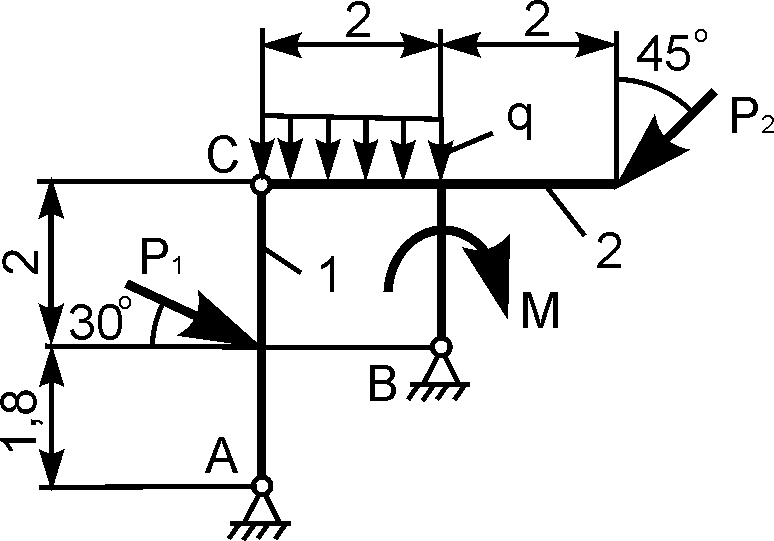
Статически неопределимые задачи – задачи, в которых реакции внешних связей не могут быть найдены из уравнений статического равновесия, составленных для данной механической системы.
Для балки (рис. 1.61) можно составить только три уравнения равновесия, в которые входят четыре неизвестные реакции XA, YA, XB, YB.
Рис. 1.61
Дано: Р, М, q. Определить реакции внешних связей в точках А и В.
Подробное решение такой задачи (статически неопределимой) рассматривается в курсе сопротивления материалов.
1.23. Алгоритм решения задач на определение реакций внешних связей для составных конструкций
Существует целый класс задач на равновесие составной конструкции, которые могут быть решены методами статики твердого тела. Решение таких задач проводится по следующему алгоритму.
Выбирается система отсчета.
Выделяется механическая система (составная конструкция), равновесие которой рассматривается.
К механической системе прикладываются активные нагрузки. Если задана распределенная нагрузка, то она приводится к сосредоточенной силе.
Согласно аксиоме связей внешние связи, наложенные на механическую систему, отбрасывают, и действие их заменяют соответствующими реакциями.
Записываются уравнения равновесия, соответствующие системе сил, действующей на составную конструкцию (система активных сил и реакций внешних связей).
Установив, что число неизвестных реакций внешних связей превышает число уравнений равновесия, составную конструкцию расчленяют по внутренним связям.
Рассматривают равновесие каждого из тел составной конструкции, которое находится в покое под действием активных сил, реакций внешних связей и реакций внутренних связей.
Для каждого из тел конструкции записывают соответствующие уравнения равновесия.
Полученную систему уравнений решают в наиболее удобной последовательности и находят неизвестные реакции внешних и внутренних связей.
Обычно при расчете используются не все уравнения равновесия, составленные для механической системы и для каждого из тел в отдельности. Поэтому оставшиеся уравнения используют для проверки полученных результатов.
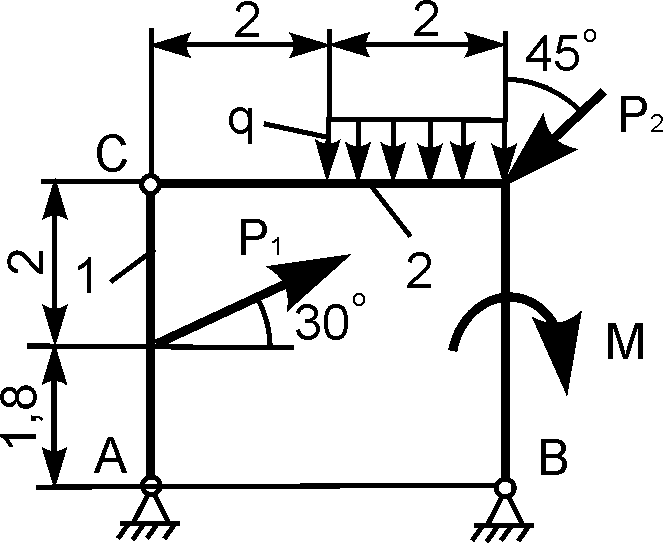
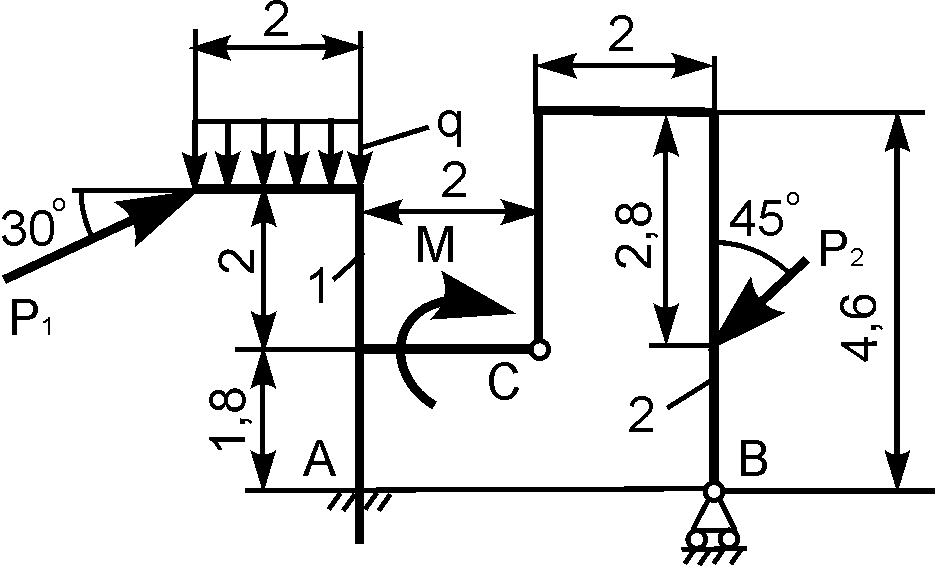
1.24. Варианты курсового задания с 3 «Определение реакций опор составной конструкции (система двух тел)»
Методологию расчета реакций внешних связей, наложенных на составную конструкцию, рассмотрим на примере выполнения курсового задания С 3, которое входит в контрольную работу обучающегося.
Конструкция состоит из двух тел. Определить реакции внешних связей, наложенных на составную конструкцию. Варианты расчетных схем конструкций и приложенные к ним нагрузки приведены в табл. 1.3.
Таблица 1.3
|
Номер варианта |
Расчетная схема |
Исходные данные |
Определяемые величины |
|
1 |
2 |
3 |
4 |
|
1 |
|
Р1 = 10 кН; Р2 = 10 кН; М = 6 кН·м; q = 2 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
Продолжение табл
. 1.3
|
1 |
2 |
3 |
4 |
|
2 |
|
Р1 = 6 кН; Р2 = 10 кН; М = 12 кН·м; q = 1 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
|
3 |
|
Р1 = 8 кН; Р2 = 10 кН; М = 3 кН·м; q = 2 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
|
4 |
|
Р1 = 5 кН; Р2 = 12 кН; М = 4 кН·м; q = 2 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
|
5 |
|
Р1 = 6 кН; Р2 = 8 кН; М = 3 кН·м; q = 2 кН/м
|
XA = ? YA = ? MA = ? RВ = ?
|
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
6 |
|
Р1 = 4 кН; Р2 = 6 кН; М = 10 кН·м; q = 2 кН/м
|
RA = ? XB = ? YВ = ? MВ = ?
|
|
7 |
|
Р1 = 7 кН; Р2 = 8 кН; М = 15 кН·м; q = 2 кН/м
|
RA = ? XB = ? YВ = ? MВ = ?
|
|
8 |
|
Р1 = 8 кН; Р2 = 8 кН; М = 16 кН·м; q = 2 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
|
9 |
|
Р1 = 10 кН; Р2 = 10 кН; М = 6 кН·м; q = 2 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
10 |
|
Р1 = 10 кН; Р2 = 3 кН; М = 9 кН·м; q = 2 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
|
11 |
|
Р1 = 12 кН; Р2 = 5 кН; М = 6 кН·м; q = 1 кН/м
|
RA = ? XB = ? YВ = ? MВ = ?
|
|
12 |
|
Р1 = 11 кН; Р2 = 3 кН; М = 8 кН·м; q = 4 кН/м
|
RA = ? XB = ? YВ = ? MВ = ?
|
|
13 |
|
Р1 = 10 кН; Р2 = 12 кН; М = 8 кН·м; q = 2 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
14 |
|
Р1 = 10 кН; Р2 = 2 кН; М = 12 кН·м; q = 2 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
|
15 |
|
Р1 = 15 кН; Р2 = 10 кН; М = 5 кН·м; q = 2 кН/м
|
XA = ? YA = ? MA = ? RВ = ?
|
|
16 |
|
Р1 = 16 кН; Р2 = 10 кН; М = 4 кН·м; q = 1 кН/м
|
XA = ? YA = ? MA = ? RВ = ?
|
|
17 |
|
Р1 = 17 кН; Р2 = 3 кН; М = 6 кН·м; q = 6 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
18 |
|
Р1 = 18 кН; Р2 = 9 кН; М = 4 кН·м; q = 8 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
|
19 |
|
Р1 = 19 кН; Р2 = 7 кН; М = 12 кН·м; q = 2 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
|
20 |
|
Р1 = 20 кН; Р2 = 12 кН; М = 8 кН·м; q = 4 кН/м
|
XA = ? YA = ? MA = ? RВ = ?
|
|
21 |
|
Р1 = 21 кН; Р2 = 10 кН; М = 12 кН·м; q = 6 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
22 |
|
Р1 = 22 кН; Р2 = 12 кН; М = 10 кН·м; q = 5 кН/м
|
XA = ? YA = ? MA = ? RВ = ?
|
|
23 |
|
Р1 = 23 кН; Р2 = 9 кН; М = 5 кН·м; q = 8 кН/м
|
RA = ? XB = ? YВ = ? MВ = ?
|
|
24 |
|
Р1 = 24 кН; Р2 = 10 кН; М = 12 кН·м; q = 2 кН/м
|
XA = ? YA = ? MA = ? RВ = ?
|
|
25 |
|
Р1 = 25 кН; Р2 = 10 кН; М = 8 кН·м; q = 2 кН/м
|
XA = ? YA = ? MA = ? RВ = ?
|
Продолжение табл. 1.3
|
1 |
2 |
3 |
4 |
|
26 |
|
Р1 = 26 кН; Р2 = 16 кН; М = 6 кН·м; q = 6 кН/м
|
RA = ? XB = ? YВ = ? MВ = ?
|
|
27 |
|
Р1 = 27 кН; Р2 = 10 кН; М = 4 кН·м; q = 3 кН/м
|
XA = ? YA = ? XВ = ? YВ = ?
|
|
28 |
|
Р1 = 28 кН; Р2 = 18 кН; М = 8 кН·м; q = 2 кН/м
|
XA = ? YA = ? MA = ? RВ = ?
|
|
29 |
|
Р1 = 28 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м
|
XA = ? YA = ? MA = ? RВ = ?
|
Окончание табл. 1.3
|
1 |
2 |
3 |
4 |
|
30 |
|
Р1 = 30 кН; Р2 = 20 кН; М = 6 кН·м; q = 1 кН/м
|
RA = ? XB = ? YВ = ? MВ = ?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|