1.21.2. Аналитический и графический способы вырезания узлов

П

Рис. 1.52

ри использовании способа вырезания узлов вырезают узел фермы и прикладывают к нему: активные силы; реакции внешних связей; реакции стержней и составляют уравнения равновесия сил, приложенных к узлу фермы. Так как в начале расчета фермы неизвестно какие стержни растянуты и какие сжаты, то условно принимается, что все стержни растянуты (т. е. реакции стержней направлены от узлов). Если в результате вычислений получают ответ со знаком минус, то соответствующий стержень сжат. Найденные реакции стержней равны по модулю внутренним усилиям в стержнях. Последовательность вырезания узлов определяется условием, что число неизвестных сил, приложенных к узлу, не должно превышать число уравнений равновесия сил (двух для плоской системы сил и трех для пространственной).

Рассмотрим изображенную на рис. 1.52 плоскую ферму, загруженную сосредоточенными силами F₁, F₂, F₃.

Рис. 1.52

Дано: F₁ = 4 кН; F₂ = 9 кН; F₃ = 2 кН; a = 2 м; α = 30⁰.

В этой ферме требуется определить реакции опор фермы, а также внутренние усилия S_i в стержнях способом вырезания узлов. Дополнительно требуется определить реакции S₇, S₈, S₉ в трех стержнях фермы способом Риттера.

Решение.

А. Определение реакций ra, xb, yb внешних связей

Порядок решения задач статики приведен в подразделе 1.7 данного пособия. Рассматривается равновесие всей фермы как абсолютно твердого тела. Как правило, выбирается правая система отсчета XOY. К ферме прикладываются активные силы F₁, F₂, F₃. Отбрасывается связь в точке А. Так как к шарнирно неподвижной опоре в точке А присоединяется один стержень, который может быть или растянут или сжат, то линия действия реакции R_A направлена вдоль стержня. К шарнирно неподвижной опоре в точке В подсоединяется три стержня, поэтому линия действия реакции R_B заранее неизвестна и, следовательно, эту реакцию раскладывают на ее составляющие X_В, Y_В по координатным осям.

Система внешних сил (F₁, F₂, F₃, R_A, X_B, Y_B), действующих на ферму, плоская произвольная, поэтому аналитические условия ее равновесия выражаются тремя уравнениями:

 F_ix = 0 = – R_A + X_B – F₁ = 0; (1)

 F_iY = Y_B – F₂ – F₃ = 0; (2)

 M_iB = 0 = R_A(3a)tg + F₁(2a)tg – F₂2a – F₃3a = 0. (3)

Решая эту систему уравнений, получим:

из уравнения (3) R_А = (– F₁(2a)tg + F₂2a + F₃3a)(3a)tg =

= (– 4220,577 + 922 + 232)320,577) = 11,198 кН;

из уравнения (1) X_B = R_A + F₁ = 11,198 + 4 = 15,198 кН;

из уравнения (2) Y_B = F₂ + F₃ = 9 + 2 = 11,000 кН.

Если величины полученных реакций имеют знак плюс, то направление реакций внешних связей на чертеже показано правильно. При противоположном условии реакции направлены в другие стороны. Однако на чертеже исправления проводить не следует. В последующих расчетах значения реакций применяют с полученными знаками.

Б. Определение усилий в стержнях способом вырезания узлов

В

Рис. 1.53

ырезаем узел, где приложена активная силаF₃, и изображаем его на чертеже. Реакции S₁₁, S₁₂ растянутых стержней 11, 12 направлены от узла (рис. 1.53).

Система сил (F₃, S₁₁, S₁₂), действующая на узел, плоская сходящаяся. Аналитические условия равновесия такой системы сил выражаются системой уравнений:

∑ F_iХ = 0 = – S₁₂ – S₁₁cosα =0; (1)

∑ F_iY = 0 = – F₃ + S₁₁sinα =0. (2)

Р

Рис. 1.53

ешая эту систему уравнений, получим:

из уравнения (2)

S₁₁ = F₃/sinα = 2/0,5 = 4,000 кН;

из уравнения (1)

S₁₂ = – S₁₁cosα = – 4·0,866 = – 3,464 кН.

Так как значение S₁₁>0, а значение S₁₂<0, то стержень 11 растянут, а стержень 12 сжат.

Аналитический расчет сразу же следует проверить графическим построением замкнутого силового многоугольника. Система сил (F₃, S₁₁, S₁₂) уравновешенная, поэтому силовой треугольник, построенный на силах F₃, S₁₁, S₁₂, должен быть замкнут. Силовой треугольник строится в выбранном масштабе (см. рис. 1.53). Построение начинается с известной силы F₃. На силовом многоугольнике определяется истинное направление реакций растянутых стержней. Графическая проверка подтвердила, что стержень 11 растянут, а стержень 12 сжат.

Графическую проверку рекомендуется выполнять сразу же после аналитических расчетов, так как этим устраняются ошибки в последующих расчетах.

Т

Рис. 1.54

ак как теперь известны реакцииS₁₁, S₁₂ растянутых стержней, то вырезается следующий узел, где приложена активная сила F₂ (рис. 1.54).

Вырезанный узел находится в равновесии под действием сходящейся системы сил (F₂, S₁₂, S₁₀, S₉). Необходимо еще раз отметить, что реакции растянутых стержней направляются от узла. Аналитические условия равновесия вырезанного узла выражаются системой уравнений:

∑ F_ix = 0 = – S₉ + S₁₂ = 0; (1)

∑ F_iy = 0 = – F₂ + S₁₀ = 0. (2)

Из уравнения (1) S₉ = S₁₂ = – 3, 464 кН <0;

из уравнения (2) S₁₀ = F₂ = 9,000 кН >0.

Таким образом, стержень 9 сжат, а стержень 10 растянут. Этот расчет проверяется графическим построением силового многоугольника (см. рис. 1.54).

Необходимо отметить, что построение силового многоугольника начинают с известных сил F₂ и S₁₂, а точка пересечения линий действия реакций S₉, S₁₀ определит их направление и модуль. При этом если известно, что стержень сжат (стержень 12), то его реакцию (S₁₂) направляют к узлу.

Графическое построение подтвердило правильность проведенных расчетов.

Определение остальных реакций растянутых стержней проводится аналогичным способом. Результаты вычислений сводятся в таблицу.

Усилия в отдельных стержнях загруженной фермы могут оказаться нулевыми. Такие стержни принято называть нулевыми.

Рассмотрим леммы, пользуясь которыми можно определить нулевые стержни плоской фермы, не производя ее расчета.

Л

Рис. 1.55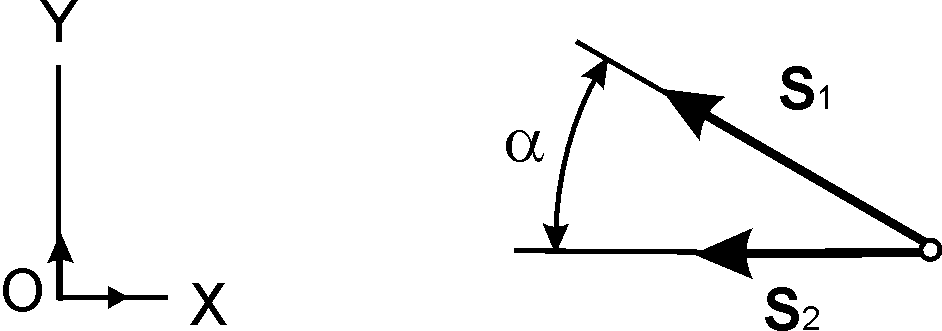

емма 1. Если в незагруженном узле плоской фермы сходятся два стержня, то усилия в этих стержнях равны нулю (рис. 1.55).

Л

Рис. 1.56

емма 2. Если в незагруженном узле плоской фермы сходятся три стержня, из которых два расположены на одной прямой, то усилие в третьем стержне равно нулю. Усилия в первых стержнях равны между собой (рис. 1.56).

Рис. 1.56

Лемма 3. Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилие в этом стержне равно по модулю приложенной внешней силе, а усилие в другом стержне равно нулю (рис. 1.57).

Рис. 1.57